BC/NW 2015 № 2 (27):5.1

АЛГОРИТМИЗАЦИЯ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДЛЯ АНАЛИЗА ПРОИЗВОДИТЕЛЬНОСТИ ВЫЧИСЛИТЕЛЬНОЙ СЕТИ РЕАЛЬНОЙ РАЗМЕРНОСТИ

Абросимов Л. И.

Разработка и модернизация эффективно функционирующих региональных и корпоративных сетей ЭВМ является сложным и трудоемким процессом, так как разработчику необходимо учитывать много критериев эффективности, большое количество ограничений, широкий спектр разнообразный устройств, каждое из которых обладает индивидуальным набором технических характеристик, которые часто зависят от местоположения и взаимосвязей с другими устройствами. (см. рис. 1)

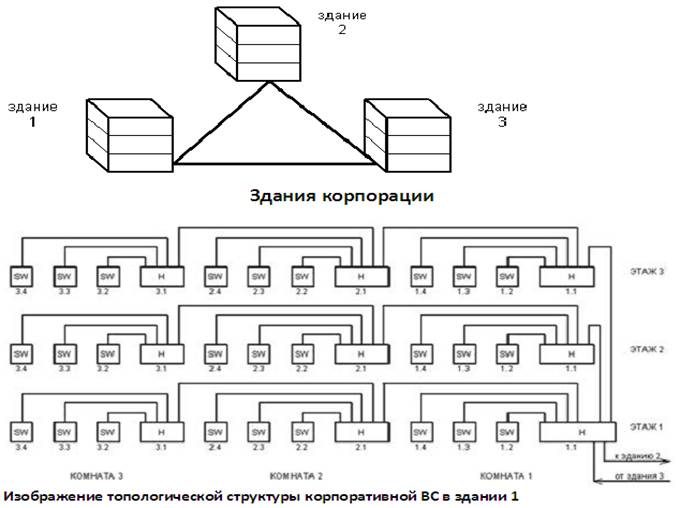
Рис.1. Пример структуры Корпоративной ВС

Кроме того, особенностью современных вычислительных сетей (ВС) является рост потока заявок на обслуживание.

Разработчику приходится постоянно сталкиваться со следующими до сих пор не решенными проблемами.

· Необходимость упорядочить и постоянно обновлять исходные данные, которые могут понадобиться при разработке сетей ЭВМ

· Необходимость согласовать производительность ВС с постоянно возрастающими требованиями пользователей для обеспечения качественного обслуживания пользователей.

· Необходимость определять производительность и выявлять узкие места для различных типов топологий и архитектур сетей ЭВМ

· Необходимость использовать и согласовать между собой адаптивные методы и модели, обеспечивающие количественное обоснование проектных решений.

Для успешного решения указанных проблем необходима компьютеризация не только процессов хранения и поиска данных, но и процессов построения моделей.

Для оценки производительности ВС необходимы модели, которые, во-первых, учитывают реальную размерность ВС, во-вторых, базируются на аналитических соотношениях, которые позволяют оперативно и детально оценивать предельную производительность ВС, в третьих, позволяют однозначно, с необходимой детализацией соотносить результаты, определенных для элементов моделирования, с параметрами устройств ВС.

Таким требованиям удовлетворяет модели, построенные с использованием метода контуров [1], в котором последовательно выполняются: описание топологической структуры ВС; построение функциональной структуры ВС; формализованного детализированного описания потока заявок на обслуживание; составление и решение линейных и нелинейных уравнений для определения требуемых вероятностно-временных характеристик функционирования ВС.

Для создания полностью автоматизированной процедуры требуется решить задачу изоморфного преобразования топологической, логической и функциональной структур ВС, а именно:

o сформулировать правила логических преобразований и формализовано записать топологическую структуру ВС в форме топологической матрицы Т ;

o сформулировать правила логических преобразований матриц Т в L и формализовано записать логическую структуру в форме логической матрицы L;

o сформулировать правила логических преобразований матриц Т и L в F и формализовано записать функциональную структуру в форме функциональной матрицы F;

o определить требуемые функциональные характеристики.

Кратко рассмотрим состав и последовательность выполняемых действий (компьютеризированных процедур) при разработке и модернизации региональных и/или корпоративных ВС.

Подготовительные процедуры.

1. Формирование базы данных технических и программных средств (БДС), в результате которого получают:

§ классификации устройств (У), линий связи (ЛС) и программного обеспечения (ПО);

§ технические характеристики У, Л, и ПО;

§ Экономические характеристики У, Л, и ПО.

2. Формирование базы данных трафика (БДТ), в результате которого получают:

§ классификации клиентов и серверов;

§ схема взаимодействия клиентов и серверов;

§ информационные характеристики взаимодействия;

Процедуры, выполняемые при разработке ВС.

3. Разработка принципиальной схемы соединения устройств посредством линий связи, с указанием идентификаторов (A.r),(B.k) и типов устройств, типов линий связи и каналов связи. При выборе структуры используется один из алгоритмов расчета кратчайших структур, рассмотренный в [1]

Разработанная принципиальная схема ВС может быть представлен в виде визуального отображения на экране монитора разработчика и в виде списка соединений устройств линиями связи.

Для обеспечения изоморфизма топологической, логической и функциональной моделей при выполнении формирования и преобразования матричных представлений моделей используется массив М метаданных, который состоит из набора таблиц 1М, 2М, 3М, 4М.

4. Формирование топологической матрицы Т, которое выполняется по соотношению (1) и отображает все физические элементы ВС, к которым относятся устройства множества У (рабочие станции, серверы, коммутирующие устройства) и множества Л (линий связи).

(1)

где w - тип устройства, А и В – идентификатор, определяющий местоположение У У, R – количество разъемов в устройстве У, - тип линии связи Л Л (физическая реализация), - тип канала связи Л (дуплексный, полудуплексный, симплексный).

В таблице метаданных 1М каждому идентификатору ставится в соответствие порядковый номер i.

5. Формирование логической матрицы L, которая предназначена для отображения узлов, соответствующих тем устройствам, представленным в матрице Т, которым в ВС присвоены логические имена, адреса и номера интерфейсов.

Множество узлов U, отображаемых в матрице L, является подмножеством устройств У (U У), описываемых в топологической матрице Т, поэтому каждому узлу U_A соответствует устройство У_А.

Для описания логического соединения узлов U , соответствующих ВС, используются дуги D, которые могут быть взвешены в соответствии с выбранной метрикой маршрутизации.

Основным параметром дуги D является тип γ канала связи, организованного между узлами U_A и U_В.

На основании матрицы Т, списков {U} и {D} можно сформировать матрицу L логической структуры, в которой:

(2)

В таблице метаданных 2М каждому идентификатору и B ставится в соответствие порядковый номер i.

6. Решение задачи выбора кратчайших маршрутов, используя данные логической матрицы L и выбранный критерий эффективностью. Результатом расчета является таблица маршрутизации между всеми адресуемыми устройствами ВС.

7. Формирование функциональной матрицы F, которая является основой математической модели ВС и предназначена для отображения функциональных элементов Е, соответствующих устройствам У и линиям Л, которые задерживают транзакции при обработке и оказывают существенное влияние на производительность ВС.

Каждый элемент Е описывается соотношениями моделей массового обслуживания, является ориентированным и имеет вход (1) и выход (2). Подмножество ЕУЕ является подмножеством элементов отображающих У и каждый элемент ЕА подмножества ЕУ имеет идентификатор А, введенный при формировании топологической структуры. Для устройств и элементов используется одна и та же система индикаторов. Подмножество ЕКЕ является подмножеством элементов отображающих каналы К и каждый элемент ЕК подмножества ЕК имеет идентификатор (А.k-B.r).

Для формирования матрицы F необходимо использовать множество ES переходов, отображающих соединение выходов (2) элементов подмножеств ЕУ с входами (1) элементов подмножества ЕК и соединение выходов (2) элементов подмножеств ЕК с входами (1) элементов подмножества ЕУ.

На основании матрицы Т, можно сформировать матрицу F функциональной структуры, в которой

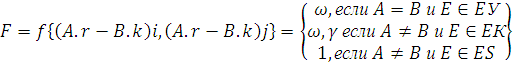(3)

где i и j – соответственно, строки и столбцы в матрице F, а r и k – разъемы устройств А и В.

В таблице метаданных 3М каждому идентификатору устройства А-А и каждому идентификатору линии связи ставится в соответствие порядковый номер элемента Е, а каждому входу/выходу элемента Е ставится в соответствие порядковый номер j.

8. Определение состава контуров , каждый из которых представляет маршрут потока заявок в виде последовательности номеров {i}элементов ЕУ и ЕК, которые моделируют интенсивность обслуживания узлами и линиями ВС потока заявок, поступающих на обслуживание с интенсивностью . Для формирования состава контура используется таблица маршрутизации между всеми адресуемыми устройствами ВС, которая дополняется элементам ЕК , которые не являются адресуемыми элементами. Для решения задачи используется модифицированная методика выбора кратчайших маршрутов [1].

9. Формирование линейных уравнений (ЛУ) состоит в использовании для каждого элемента контура qQ , составленного в соответствии с [1].

10. В связи с использованием единственного кратчайшего маршрута в результате решения ЛУ для каждого контура qQ все коэффициенты базовой интенсивности равны 1,0 т.е.:

(4)

11. При формировании системы нелинейных уравнений (НЛУ) для каждого замкнутого контура qQ, в котором по маршруту перемещается заявок, используется соотношение (5), если элемент моделируется СМО М/М/1/:

, где (5)

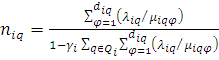, где

– маршрут потока заявок контура qQ

– множество контуров, обслуживаемых элементом ;

- количество фаз обработки контура q элементом ;

Количество уравнений равно числу контуров .

12. Решение системы НЛУ для ВС произвольной конфигурации целесообразно производить, используя метод тангенсов, рассмотренный в [1 ]. В результате решения НЛУ получаем значения базовых интенсивностей .для каждого контура .

13. Определение функциональных характеристик моделируемой ВС.

Среднее время доставки сообщений контура q в разомкнутой сети:

(6)

Среднее время отклика сообщений замкнутого контура q, содержащего сообщений, каждое из которых генерируется i-м элементом:

(7)

Коэффициент загрузки элемента i интенсивностями соответствующих контуров :

(8)

Следует подчеркнуть, что приведенные функциональные характеристики определены для функциональной модели ВС. Однако, выполненные преобразования матриц Т, L, F обладают изоморфизмом, т.е. каждому элементу функциональной матрицы F соответствует техническая реализация в виде устройства или линии связи которые занесены в базу данных БДС, поэтому для повторного расчета требуется меньше вычислительных ресурсов.

Пример, в котором номера выполняемых действий указаны в фигурных скобках {}

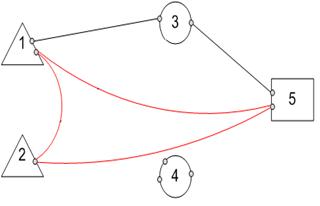
В качестве примера рассмотрим изображенный на рис. 2 фрагмент принципиальной схемы корпоративной ВС, который состоит из 5-ти устройств: рабочих станций A = 1,2; (=1), сервера A=5; (=2), адресуемого коммутатора A=3; (=3), неуправляемого коммутатора A=4 (=3). {1}

В диалоговом режиме взаимодействуют: рабочая станция (A = 1) и сервер (A=5); рабочая станция (A = 2) и сервер (A=5); рабочая станция (A = 1) и рабочая станция (A = 2).

В качестве Л, соединяющей У, используется витая пара ( =1), протокол передачи данных – дуплексный канал (=1). {1}

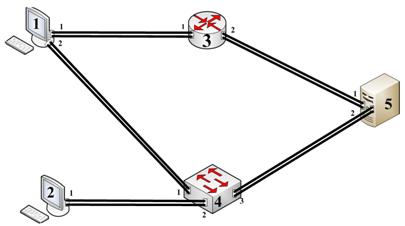
Рис.2. Фрагмент принципиальной схемы корпоративной ВС {2}

Таблица 1М {3}

(A,r)	1.1	1.2	2.1	3.1	3.2	4.1	4.2	4.3	5.1	5.2
i	1	2	3	4	5	6	7	8	9	10

		1	2	3	4	5	6	7	8	9	10
	1	1,2			1,1
	2		1,2				1,1
	3			1,1				1,1
	4	1,1			3,2,
Т=	5					3,2				1,1
	6		1,1				4,3
	7			1,1				4,3
	8								4,3		1,1
	9					1,1				2,2
	10								1,1		2,2

Рис. 3. Матрица T топологической структуры ВС{4}

В качестве примера на рис. 4. изображена матрица L логической структуры для фрагмента корпоративной ВС, изображенного на рис.2 . {5}

На рис. 5 изображены дуги, отображающие наличие соединения между узлами 1 и 3, которые соответствуют устройствам 1(рабочей станции) и 3(серверу), изображенным на рис.2. Как видно из рис. 5, дуги отображают также наличие логических соединений между узлами 1 и 3, организованных по нескольким (двум) линиям связи, соединенным через коммутатор 4, который не вошел в состав логического описания ВС, так как он не имеет логического адреса.

Таблица 2М {5}

А	1	2	3	5
i	1	2	3	4

		1	2	3	4
	1	1	1	1	1
L	2	1	1		1
	3	1		3	1
	4	1	1	1	2

Рис.4. Матрица L

логической структуры ВС{5}

Рис. 5. Дуги между узлами в логической структуре ВС{5}

В рассматриваемом примере в диалоговом режиме взаимодействуют устройства:

1 и 5 , что соответствует контуру q=1;

2 и 5 , что соответствует контуру q=2;

1 и 2 , что соответствует контуру q=;

Решение задачи выбора кратчайших маршрутов {6} по матрице L позволяет определить состав устройств, участвующих в каждом маршруте:

Номера контуров	Номера устройств, входящих кратчайший маршрут
q = 1	1 – 3 – 5 – 3 – 1
q = 2	2 – (4) – 5 – (4) – 2
q = 3	1 – (4) – 2 – (4) – 1

В качестве примера на рис.6 показана функциональная структура ВС, {7}которая отображает функциональные элементы Е, соответствующие устройствам У и линиям Л, которые задерживают потоки заявок при обработке и оказывают существенное влияние на производительность ВС. Для фрагмента корпоративной ВС, изображенного на рис.2, на рис.6 представлена матрица F функциональной структуры. {6}

Для автоматизации преобразования матриц необходимо решить 2 задачи:

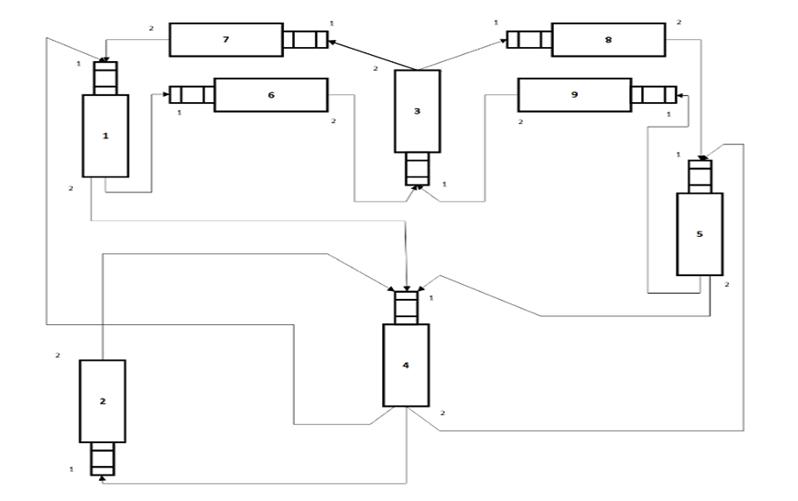
Рис.6 Функциональная структура ВС

Таблица 3М

	(1-1)1	(1-1)2	(2-2)1	(2-2)2	(3-3)1	(3-3)2
(E)	(1)1	(1)2	(2)1	(2)2	(3)1	(3)2
i	1	2	3	4	5	6
	(4-4)1	(4-4)2	(5-5)1	(5-5)2	(1.2-3.1)1	(1.2-3.1)2
(E)	(4)1	(4)2	(5)1	(5)2	(6)1	(6)2
i	7	8	9	10	11	12
	(3.2-1.1)1	(3.2-1.1)2	(3.2-5.1)1	(3.2-5.1)2	(5.2-3.1)1	(5.2-3.1)2
(E)	(7)1	(7)2	(8)1	(8)2	(9)1	(9)2
i	13	14	15	16	17	18

Для автоматизации преобразования матриц необходимо решить 2 задачи:

1). Преобразовать матрицу Т топологической структуры в матрицу L логической структуры. {7}

2). Преобразовать матриц топологической Т и логической L структур в матрицу F функциональной структуры. {7}

		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
	1		1
	2							1				1
	3				1
	4											1
	5						3
	6													1		1
	7								4
F=	8	1		1						1
	9							1			2							1
	10
	11												1
	12					1
	13														1
	14	1
	15																1
	16
	17																		1
	18					1

Рис.7. Матрица функциональной структуры F

В матрице F в диагональные ячейки с1 по 10 записаны значения ; в диагональные ячейки c 11 по 18 записаны значения - (тип линии связи Л Л) .. Численные значения типов соответствуют принятым для примера классификациям. {7}

Чтобы определить состав элементов ЕУ и ЕК, {8} входящий в каждый контур, решается задача поиска кратчайших маршрутов, в которой исходные данные для метрики расстояний определяются матрицей функциональной структуры F и кратчайшими маршрутами матрицу L {8}.

При формировании системы нелинейных уравнений {10, 11} в состав контура q = 1 входят элементы маршрута W(q = 1) => 1, 6, 3, 8, 5, 9, 3, 7, 1;

в состав контура q = 2 входят элементы маршрута W (q = 2) => 2, 4, 5, 4, 2;

в состав контура q = 3 входят элементы маршрута W (q = 3) => 1, 4, 2, 4, 1.

При формировании уравнений по соотношению (5) {11} следует подчеркнуть, что в рассматриваемом примере элемент 1 входит в контура q = 1 и q = 3 ; элемент 2 входит в контура q = 2 и q = 3 ; элемент 5 входит в контура q = 1 и q = 2.

Изложенные компьютеризированные процедуры реализованы в виде программных модулей, которые успешно прошли первые тесты.

Литература

1 Абросимов Л.И. Базисные методы проектирования и анализа сетей ЭВМ: учебное пособие / Л.И. Абросимов. – М.: Университетская книга, 2015. – 248 с. – ISBN 978-5-98699-153-5.