BC/NW 2016 № 1 (28):10.3

ПРИМЕНЕНИЕ ТЕНЗОРНОЙ АППРОКСИМАЦИИ И ЗАРАНЕЕ ВЫЧИСЛЕННОГО СЛОВАРЯ ДЛЯ СЖАТИЯ ИЗОБРАЖЕНИЙ И ВИДЕО

Макаров Д.В., М.К. Чобану М.К.

В настоящее время требования к качеству контента мультимедиа постоянно растут, а с ростом качества возрастает и размер изображений и видео [1]. Кроме того, с появлением новых типов контента (трехмерное телевидение, мультивидовое видео и т.д.) возникла проблема эффективного представления и сжатия многомерного сигнала [2].

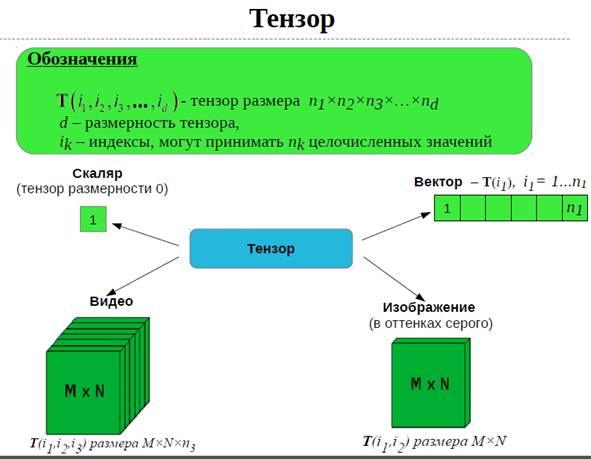
Тензорный анализ и теория тензорных аппроксимаций играют все более важную роль в области вычислительной математики и численного анализа. Эффективное представление d-мерного тензора (массива с d индексами) небольшим числом параметров может дать возможность работать с данными размерности d, равной 10, 100 или даже 1000 (такие проблемы возникают в квантовой молекулярной динамике, финансовом моделировании, при решении стохастических уравнений в частных производных). В условиях экспоненциального роста объемов передачи, хранения и обработки визуальной информации [1] применение данного подхода оправдано.

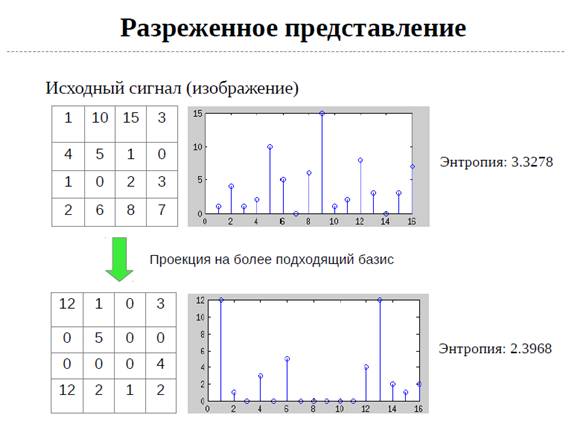
Тензорные методы являются новым направлением и находят все большее применение в цифровой обработке сигналов. Применение тензорных методов может стать хорошей альтернативой имеющимся подходам в сжатии изображений и видео.

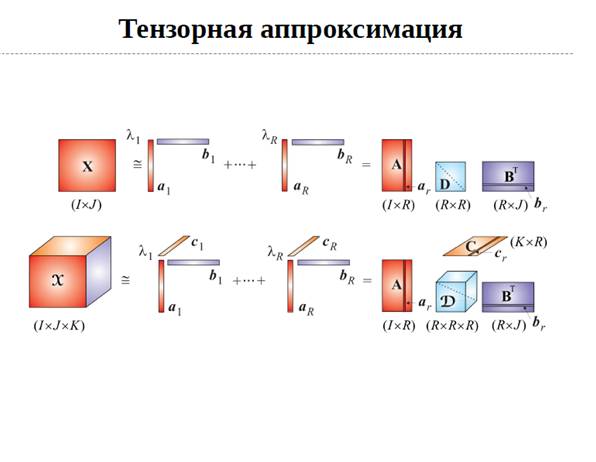
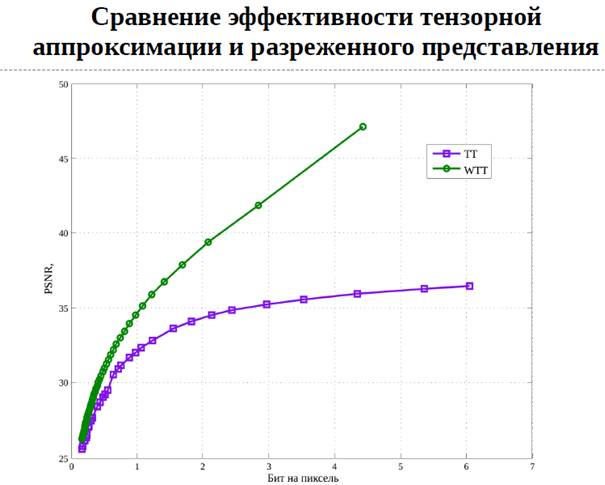
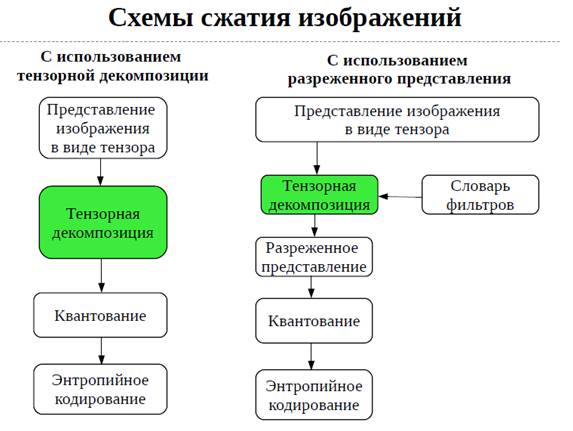
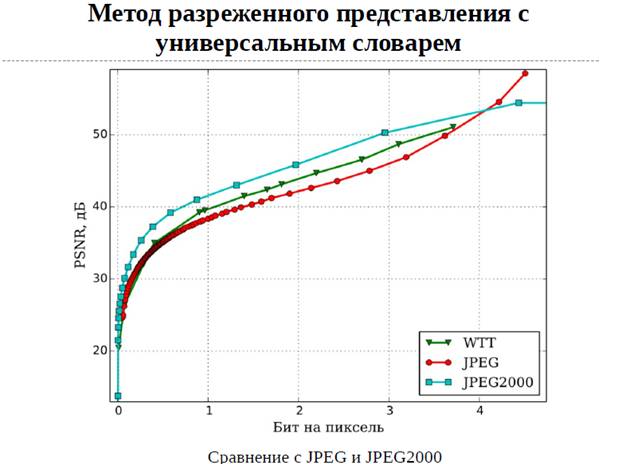
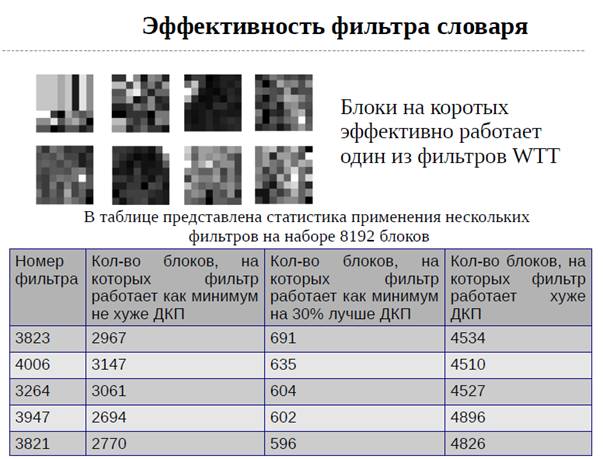
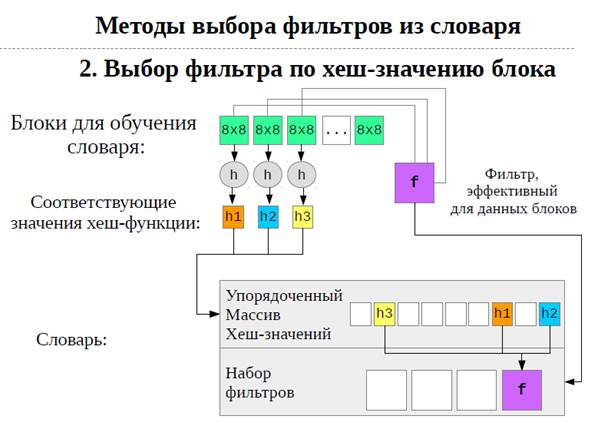
В работе рассмотрен метод Tensor-Train Decomposition [3] и Wavelet Tensor-Train (WTT [4]). Показана эффективность применения данных методов и рассмотрена возможность обучения словаря фильтров WTT для повышения эффективности сжатия.

 Эффективность методов представлена в сравнении с дискретным косинусным преобразованием (применяемом в алгоритме сжатия JPEG). Также предложено решение для повышения эффективности современных алгоритмов сжатия видео.

Литература

1. Дворкович В., Чобану М. Проблемы и перспективы развития систем коди-

рования динамических изображений // MediaVision. 2011. № 2. С. 55—64.

2. Чобану М. Многомерные многоскоростные системы обработки сигналов.

М.: Техносфера, 2009. 480 c.

3. Oseledets I.V. Tensor-train decomposition // SIAM J. Sci.Comput. 2011. Vol. 33.

No. 5. Р. 2295—2317.

4. Oseledets I.V., Tyrtyshnikov E.E. Algebraic wavelet transform via quantics tensor

train decomposition // INM RAS. 2010. Preprint 2010-03.__