BC/NW 2016 № 1 (28):8.1

АЛГОРИТМ ОПРЕДЕЛЕНИЯ ТОПОЛОГИИ ОТКАЗОУСТОЙЧИВОЙ VPN, С МИНИМАЛЬНО ЗАНИМАЕМОЙ ДОПОЛНИТЕЛЬНОЙ ПОЛОСОЙ ПРОПУСКАНИЯ В СЕТИ

В.О. Рыбинцев, Д.Г.Данилин

Предварительные замечания

Одной из наиболее важных задач, стоящих перед технологией VPN,  является проблема обеспечения качества обслуживания QoS. Проблема обеспечения гарантированного QoS для технологииVPN усложняется  тем, что трафик данных принимает все более и более мультимедийный характер.  Решить данную задачу можно только выделением сетевых ресурсов для соответствующих потоков трафика. Здесь возникает определенное противоречие: пользователи хотят получить услуги с гарантированным качеством и  минимально возможной стоимостью, а провайдер желает обеспечить максимальную загрузку сети и получить максимальный доход. Поэтому задача обеспечения гарантированного QoS для каждого пользователя превращается в задачу оптимального распределения сетевых ресурсов провайдера.

Для VPN задача оптимального распределения ресурсов вырождается в задачу выбора набора маршрутов, соединяющих сайты VPN между собой, и выделения на них соответствующих ресурсов. При этом предполагается, что выделенные ресурсы имеют минимально возможную стоимость. Под стоимостью в данной конкретной задаче следует понимать затрачиваемую полосу пропускания, необходимую для построения VPN – сети.

В литературе предложено несколько моделей оптимального распределения ресурсов VPN с целью обеспечения заданного качества обслуживания в VPN. Общепринятыми являются две модели - канальная модель (pipemodel) и потоковая модель (hose-model) (1).

Одной из задач, связанных с QoS [2] является отказоустойчивость VPN. Под отказоустойчивостью  понимается способность VPN скрывать от пользователей отказ отдельных ее элементов (звеньев или узлов сети).

В общем случае задача обеспечения отказоустойчивости VPN предполагает определение набора возможных обходных маршрутов для того или иного набора отказавших ресурсов и выбор оптимального варианта по критерию минимальной стоимости. Для уменьшения вычислительной сложности задачи, как правило, рассматривается отказ только одного типа ресурса - звена данных, связывающего два смежных узла сети. В дальнейшем путь, по которому передается трафик VPN в обход отказавшего звена или узла, будем называть запасным или защитным, а выделенную на звеньях этого пути полосу пропускания - защитной полосой пропускания.

Постановка задачи

Прежде чем формулировать задачу построения отказоустойчивых VPN, введем два упрощения. Во-первых, в постановке задачи будет рассматриваться отказ только одного типа сетевого ресурса - звеньев сети. Во-вторых, звенья сети имеют бесконечную пропускную способность.

Пусть имеется исходная сеть, заданная в виде графа G(V,E).  Множество вершин графа V соответствует узлам сети, а множество ребер графа E соответствует звеньям сети. Предположим, что на ресурсах этой сети организована VPN произвольной структуры, заданная графом GVPN(V’,E’), для которого справедливо V’ V, E’  E. На каждом ребре е=(u,v)  графа GVPN(V’,E’) выделена необходимая полоса пропускания b(u,v). Важным является то, что конечные точки VPN связаны между собой. Пусть одновременно могут отказать не более чем k ребер (k ограничено количеством самих ребер VPN), причем до того момента, как откажут другие ребра, работоспособность этих k ребер будет восстановлена. Пусть F  E’ множество отказавших ребер в данный момент, а R– множество защитных ребер для данного множества отказавших ребер F.

Таким образом, задано:

- граф сети G(V,E), содержащий V вершин и E ребер;

- сеть VPN  в виде подграфа G’(V’,E’): V’  V, E’  E;

- множество конечных точек VPN Q VT;

- число ребер, которые могут отказать одновременно k;

- множество отказавших ребер F  E’, |F|≤k:

- полоса пропускания, выделенная на каждом ребре дерева VPN b(u,v).

Требуется:

Для любого F найти множество R и выделенную на каждом ребре (u,v)  защитную полосу пропускания bдоп (u,v) так, чтобы между любыми  конечными точками VPN i и j существовал путь Pij  (GVPN – F)  R ≠ О. При этом суммарная дополнительная полоса  пропускания должна быть  

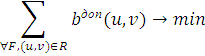
Пропускной способности, выделенной на ребрах, должно быть достаточно для успешной реализации запросов любой допустимой матрицы трафика VPN. Данная постановка задачи формально подходит для всех возможных разновидностей  потоковой моделей VPN. Конкретные модели VPN  требуют уточнения постановки задачи, так как накладывают дополнительные ограничения. Решение задачи в такой постановке должно лишь учитывать необходимость существования пути между точками подключения VPN. В данной статье рассматривается  VPN на основе асимметричной потоковой модели.

Алгоритм  определения топологии отказоустойчивой VPN, с минимальной занимаемой дополнительной полосой пропускания в сети на основе асимметричной потоковой модели.

В основе процедуры лежит алгоритм «поиска в глубину», взятый из теории графов [3]. Суть алгоритма состоит в том, что, находясь в некоторой вершине v (должны ее пометить), мы пробуем проходить по ребрам, смежным с этой вершиной, проверять, были ли мы на обратной стороне этого ребра раньше и вновь запускать с обратной стороны алгоритм поиска, до тех пор  пока не найдем нужную вершину u. Найденную вершину мы добавим в путь. Поиск в глубину (depth-first search) является одним из методов систематического обхода вершин графа. Стратегия поиска в глубину, как следует из ее названия, состоит в том, чтобы идти «вглубь» графа, насколько это возможно. При выполнении поиска в глубину исследуются все ребра, выходящие из вершины, открытой последней, и покидается вершина, только когда не остается неисследованных ребер — при этом происходит возврат в вершину, из которой была открыта вершина v. Этот процесс продолжается до тех пор, пока не будут открыты все вершины, достижимые из исходной. Если при этом остаются неоткрытые вершины, то одна из них выбирается в качестве новой исходной вершины и поиск повторяется уже из нее. Этот процесс повторяется до тех пор, пока не будут открыты все вершины.

Иллюстрация работы алгоритма на примере

Для наглядной демонстрации алгоритма поиска оптимальной конфигурации  и подсчета пропускной способности, выделенной на ребрах графа R, рассмотрим его реализацию на примере следующего графа:

- количество узлов исходного графа сети G(V,E) равно 9-ти;

- подграф VPN: G’(V’,E’): V’  V, E’  E;

- количество узлов подграфа VPN – 6-ть;

- значения пропускныхспособностей (ПП далее) ребер подграфа VPN указаны на рисунке  ниже:


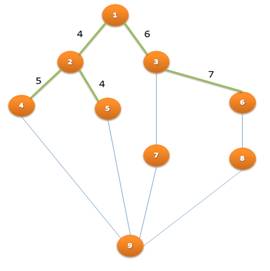
Рис.1 Реализация алгоритма поиска оптимальной конфигурации

Алгоритм решения задачи:

1)    Возьмем первое введенное ребро VPN, ребро «1-2».

Находим все обходные пути для ребра «1-2»:

a)  «1-3-6-8-9-4-2»

b)  «1-3-6-8-9-5-2»

c)   «1-3-7-9-4-2»

d)  «1-3-7-9-5-2»

2)    Выбираем один из путей последовательно по следующим критериям:

                               I.           Отбрасываем пути, содержащие ТОЛЬКО ребра подграфа VPN.

                            II.           Выбираем самый короткий по числу ребер путь (если все пути равны, то проверяем по следующему критерию)

                         III.           Выбираем путь с минимальным количеством ребер, принадлежащих подграфу VPN (если количество ребер подграфа VPN во всех путях одинаково, то проверяем следующий пункт).

                        IV.           Выбираем первый найденный путь (при выполнении пункта I, что путь НЕ должен состоять только из ребер подграфа VPN)

3)    Таким образом, выбран путь: «1-3-7-9-4-2»

4)    Всем ребрам выбранного пути, но которые не принадлежат подграфу VPN, присваиваем ПП ребра «1-2» (= «4») и запоминаем:

«1-3»: принадлежит VPN

«3-7»: присваиваем «4»

«7-9»: присваиваем «4»

«9-4»: присваиваем «4»

«4-2»: принадлежит VPN

5) Повторяем пункты 1-4 для следующего ребра VPN: «2-4».
Обходные пути для «2-4»:

a)  «2-1-3-6-8-9-4»

b)  «2-1-3-7-9-4»

c)   «2-5-9-4»

6)     Проверяем последовательно критерии п.2.

7)     Путь «2-5-9-4» – самый короткий.

8)     Присваиваем всем ребрам пути, не принадлежащим VPN,  ПП ребра «2-4» (= «5»):

«2-5»: принадлежит VPN

«5-9:» прибавляем «5» к ранее записанной «4»-ке, запоминаем «9»

«9-4»: прибавляем «5» к ранее записанной «4»-ке, запоминаем «9»

9)     Выбираем следующее ребро «2-5».

Обходные пути для «2-5»:

a)  «5-9-8-6-3-1-2»

b)  «5-9-7-3-1-2»

c)   «5-9-4-2»

10)            Проверяем критерии п.2.

11)            Выбираем путь: «5-9-4-2» (самый короткий).

12)            Присваиваем всем ребрам пути, не принадлежащим VPN,  ПП ребра «2-5» (= «4»);

«5-9»: прибавляем «4»-ку к  «9»-ке (запомнили в п.8), запоминаем «13»

«9-4»: прибавляем «4»-ку к «9»-ке (запомнили в п.8), запоминаем значение «13»

«4-2»: принадлежит VPN

13)            Берем следующее ребро «1-3».

Обходные пути для «1-3»:

a)  «3-7-9-4-2-1»

b)  «3-6-8-9-4-2-1»

c)   «3-7-9-5-2-1»

d)  «3-6-8-9-5-2-1»

14) Проверяем критерии п.2.

15) Выбираем путь: «3-7-9-4-2-1»

16) Присваиваем всем ребрам пути,  не принадлежащим  VPN,  ПП ребра «1-3» (= «6»):

«3-7»: прибавляем «6»-ку к  «4»-ке (запомнили в п.4), запоминаем «10»

«7-9»: прибавляем «6»-ку к «4»-ке (запомнили в п.4), запоминаем значение «10»

«9-4»: прибавляем «6»-ку к «13»-и (запомнили в п.12), запоминаем значение «19»

«4-2»: принадлежит VPN

«2-1»: принадлежит VPN

17) Выбираем последнее ребро «3-6» графа VPN.

Обходные пути для ребра «3-6»:

a)  «3-1-2-4-9-8-6»

b)  «3-1-2-5-9-8-6»

c)   «3-7-9-8-6»

18) Проверяем критерии п.2.

19) Выбираем путь: «3-7-9-8-6»

20) Присваиваем всем ребрам пути, не принадлежащим VPN,  ПП ребра «3-6» (= «7»):

«3-7»: к «6»-ке прибавляем «10» (см. п.16), запоминаем  значение «16»

«7-9»: к «6»-ке прибавляем «10» (см. п.16), запоминаем значение «16»

«9-8»: присваиваем «6»-ку

«8-6»: присваиваем «6»-ку

21) Проверяем, что все ребра подграфа VPN проверили.

22) Считаем суммарную пропускную способность графа R= G- G’:  т.е. ПП ребер: ПП(4-9) + ПП(5-9) + ПП(3-7) + ПП(7-9) + ПП(6-8) + ПП(8-9) = 19 + 13 + +16 + 16 + 6 + 6 = 76. Получившееся значение считается как сумма минимальных значений пропускной способности для каждого ребра графа G- G’ и поэтому является минимальным для обеспечения работоспособности VPN сети.

Аналогичный результат выдает разработанная на языке С++ по данному алгоритму программа.

Основной алгоритм программы представлен на Рис.2 .

 

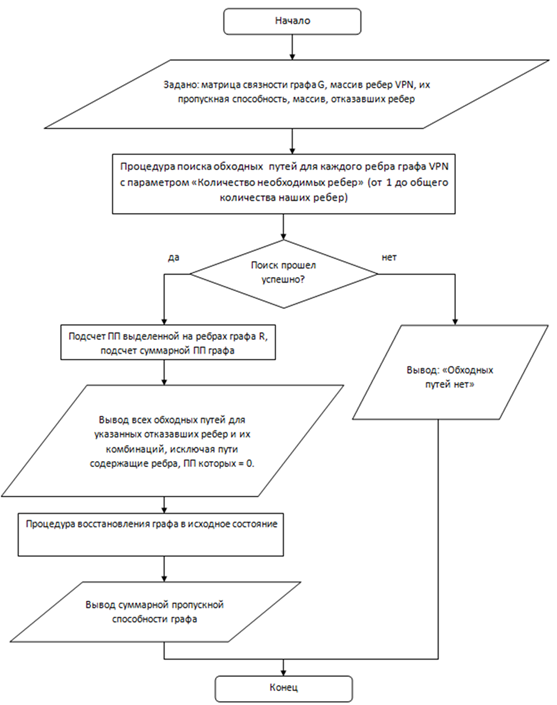
Рис.2. Основной алгоритм программы

Результаты  экспериментов

Программа, разработанная на основе описанного выше алгоритма, была  применена  к следующим  топологиям исследуемых сетей[1]:

1)       топология составное кольцо;

2)       NSFnet -   топология.

График зависимости выделенной полосы пропускания отказоустойчивого графа от числа точек VPN топологии «составное кольцо» показан на рис.3:

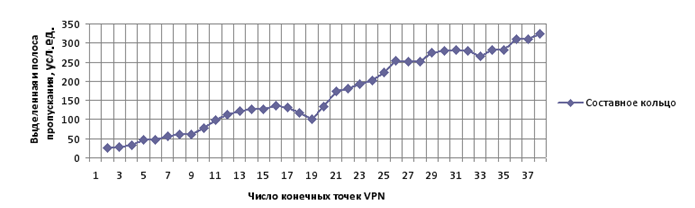
Рис.3. Полученная зависимость: Топология «Составное кольцо»

График зависимости выделенной полосы пропускания отказоустойчивого графа от числа конечных точек VPN для топологии NFSNet изображён на  рис.4.

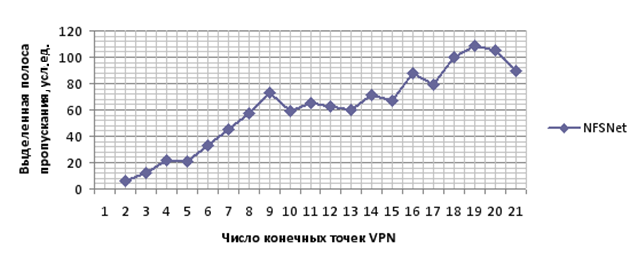
Рис.4. Полученная зависимость. Топология NFSNet

Сравнение результатов эксперимента с результатами известных ранее алгоритмов

На рис.5 приведены результаты применения разработанного алгоритма  для сетей с топологией «составное кольцо»при различном числе конечных точек VPN в сравнении с результатами, полученными  с помощью аппроксимационного алгоритма  и алгоритма резервирования «из конца в конец».  Подробнее об алгоритмах можно узнать из работ Италиано [4] и Баласубраманиама [5].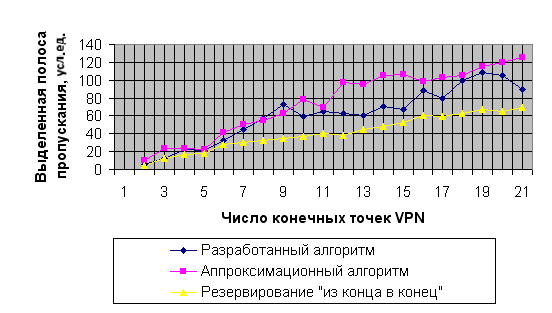

Рис. 5. Зависимость суммарной занимаемой полосы пропускания от числа конечных точек VPN  для сети с топологией «составное кольцо» для различных алгоритмов

Как видно из рисунков, наиболее эффективной является схема резервирования «из конца в конец», а наихудший результат дает аппроксимационный алгоритм. Разработанный  алгоритм, обладающий несложной реализацией,  показывает вполне хорошие результаты.

Литература

1.       Росляков, А.В. Виртуальные частные сети. Основы построения и применения / А.В. Росляков. - М.: Эко-Трендз, 2006. - 304 с.

2.    Олифер, В.Г. Компьютерные сети. Принципы, технологии, протоколы: Учебник для вузов. 3-е  изд. / В.Г. Олифер, Н.А. Олифер. - СПб.: Питер, 2016. - 992 с.

3.   Татт, У. Теория графов / У. Татт. - М.:Мир, 1998. - 424 с.

4.   Italiano G.F., Rastogi R., Yener B. Restoration Algoruthms for Virtual Private Network in the Hose Model //IEEE INFOCOM, 2002

5.   Balasubramanian A., Sasaki G. Bandwidth requirement for the protected VPNs in the hosw model // International Sympolium on Infjormation Theory. – Kanagawa, 2003