BC/NW 2016 № 1 (28):9.3

ПРИМЕНЕНИЕ УНИВЕРСАЛЬНЫХ ПРЕДСТАВЛЕНИЙ ЧИСЕЛ

ДЛЯ РЕШЕНИЯ СЛАУ

Ермилов С.И., Оцоков Ш.А.

Проблема достоверных вычислений является актуальным направлением в области теоретической информатики вследствие большого объема научных и инженерных задач [1]. Одной из таких задач является решение систем линейных алгебраических уравнений (СЛАУ). Решение СЛАУ используется в широком классе задач, таких как гидродинамика, экономика, вычислительная физика.

Универсальное представление числа (УПЧ) — это множество объектов {s,e,m,u,es,fs}, где s — знак числа, равный нулю или единице; e — порядок числа со знаком; m — мантисса без знака; u — бит неопределенности; es — размер экспоненты в битах; fs — размер мантиссы в битах.

 Введение дополнительных бит расширяет поле возможных значений формата, объединяя в едином формате возможности чисел с плавающей точкой и интервальной арифметики [2]. Арифметические операции определяются в формате с плавающей точкой, но в случае обнаружения округления значение числа за счет бита округления переходит в достоверный интервал, и дальнейшие вычисления ведутся с интервалами.

 Преимуществом УПЧ является устранение ошибок округления с помощью встроенного механизма интервальной арифметики.

Самым простым методом для решения СЛАУ является метод Гаусса. Однако метод Гаусса вычислительно неустойчив из-за недостатков чисел с плавающей точкой, что делает его не пригодным для плохо обусловленных СЛАУ вследствие ошибок округления [3].

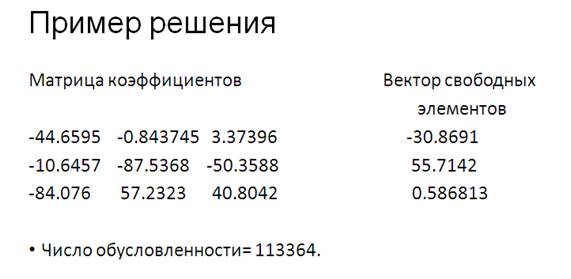
Для оценки результатов используется следующий эксперимент. Сгенерируем матрицу коэффициентов и вектор свободных членов, подсчитаем число обусловленности, получим решение тремя способами: аналитическим расчетом, методом Гаусса с плавающей точкой, методом Гаусса с УПЧ.

 Итог: при использовании УПЧ вектор решения является либо вектором с рациональными значениями, либо вектором с интервалами, содержащими внутри себя точное решение СЛАУ.

Литература

1. Bailey D.H. High-precision floating-point arithmetic in scientific computation

//Computing in science & engineering. 2005. Vol. 7. No. 3. С. 54—61.

2. Gustafson J.L. The End of Error. Unum Computing, 2015.

3. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы

для инженеров. М.: Издательство МЭИ, 2003.__