Точка внутри полигона или Дьявол кроется в деталях

Гольцов А.Г.

(Москва, каф. ВМСС, НИУ МЭИ)

Каждый человек хоть раз в жизни сталкивался с ситуацией, когда основное дело сопровождают ряд вспомогательных, по своей трудоемкости зачастую сравнимых или превышающих основное. Например, поклейка обоев сопровождается устранением дефектов стен, подгоном рисунка и креплением плинтусов, на что времени может уйти даже больше, чем собственно на основную работу с клеем и полотнищами. Примерно с такими же ситуациями периодически сталкивается программист, когда придуманный им красивый и простой алгоритм вынужденно обрастает обработкой редких и мелких частных случаев, теряя свою лаконичность и привлекательность. Рассматриваемый ниже пример показывает, что иногда из дебрей частных случаев возможно вырваться.

Рассмотрим простую задачу. На экране есть изображение с активными зонами: щелкая мышкой по тому или иному участку изображения, пользователь указывает программе, что именно с этой зоной он желает что-то сделать. Например, в медицинской программе показаны органы человека, и мышкой необходимо выбрать орган, чтобы что-то о нем прочитать. Активная зона описывается ограничивающим ее многоугольником, тот в свою очередь – набором координат вершин. Необходимо проверить условие «точка внутри полигона».

Один из известных способов решения данной задачи заключается в подсчете количества пересечений луча, проведенного из проверяемой точки в произвольном направлении, с ребрами многоугольника. Если количество пересечений четно (0, 2, 4, …), то точка лежит вне многоугольника, иначе  – внутри. В литературе для простоты рассуждений рекомендуют направлять луч вдоль осей, например, вправо по горизонтали. Попробуем.

Пусть многоугольник имеет N вершин и N ребер и описан массивом точек P={P_i}, i=1..N. Каждый элемент массива P представляет собой пару координат: P_i=(x_i, y_i). Для простоты записи  будем считать, что определен также N+1-й элемент массива P, содержащий то же значение, что и P₁. Каждое j-тое ребро задается парой элементов массива P:  R_j=(P_j,P_j+1), j=1..N.

Пусть проверяемая точка P, в которой находится мышиный курсор,  имеет координаты (x₀, y₀) (рис.1).

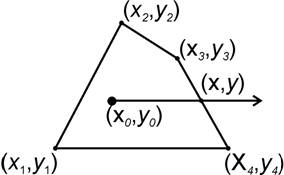
Рис.1

Луч, проведенный из точки P вправо, имеет уравнение: y = y₀ при x>x₀.

Точка (x,y) пересечения прямой, на которой лежит луч, проводимый через точку P, и прямой, на которой лежит ребро R_j, может быть вычислена путем решения простейшей системы уравнений:

y = y₀; (луч)

y = x (y_j+1–y_j)/(x_j+1–x_j) + (y_jx_j+1 – y_j+1x_j)/(x_j+1 – x_j); (ребро)

откуда (y уже известен и равен y₀)

x = (y₀(x_j+1 – x_j) – (y_jx_j+1 – y_j+1x_j) ) / (y_j+1–y_j)

Пересечение луча с ребром есть, когда выполнены сразу три условия:

· y=y₀ лежит между y_j и y_j+1 – и это можно проверить еще до вычисления x

· x лежит между x_j и x_j+1

· x>x₀

Формулы написаны, можно кодировать на языке программирования. Даже за счет горизонтальности луча дополнительно можно оптимизировать перебор ребер: если ребро целиком лежит выше или ниже проверяемой точки, это видно сразу и его можно отбросить. И тут начинаются уточнения условий…

Многоугольник и положение курсора мыши заданы в экранных координатах, которые обозначают позицию точек изображения в растровой сетке и выражаются целыми числами. Поэтому возможен вариант, когда наш элегантный горизонтальный луч пройдет точно через вершину многоугольника! За сколько пересечений считать такое прохождение через вершину? Видимо, за одно (рис.2). Хорошо, а в ситуации, показанной на рис.3? Видимо, в таком случае – за ноль (или за два). Приходится писать дополнительные проверки: находятся ли примыкающие ребра в одной полуплоскости или в разных полуплоскостях относительно луча.

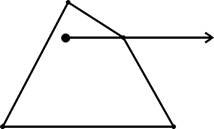
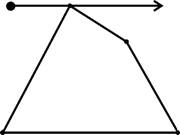
             Рис.2                                                               Рис. 3

А ведь возможна ситуация, когда пользователь щелкнул прямо по границе полигона, а она еще и горизонтальная к тому же (рис.4). Особенно интересен случай, представленный на рис.5. Что делать, как считать? Встает вопрос: а не провести ли луч куда-то действительно произвольным образом, под заданным или случайным углом к горизонту, вычисления ведь все равно ведутся в вещественной арифметике?

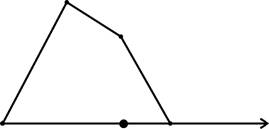
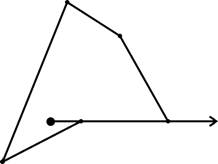
Рис. 4                                                                   Рис.5

К счастью, в рассматриваемой постановке задачи вполне возможно решить все обозначенные выше проблемы одним махом: достаточно просто принять, что, например,  щелчки мышью, принимаемые к рассмотрению, происходят не в точке с целыми координатами (x₀,y₀), а в точке с вещественными координатами (x₀+d, y₀+d), где 0<d<1, например, d = 0,5. Просто сместим координаты мыши на фиксированные полпикселя. Горизонтальный луч, проведенный на нецелом уровне y₀+d, никогда не пройдет через вершину полигона с целыми координатами (x_i,y_i) и всегда или пересечет ребро где-то между его концами, или не пересечет вовсе.

К сожалению, простые и эффективные ухищрения можно предложить далеко не для каждой сложной ситуации. Дьявол кроется в деталях.