BC/NW 2016 № 2 (29)

РАЗРАБОТКА ПРОГРАММНОЙ МОДЕЛИ ФУНКЦИОНИРОВАНИЯ КЛАСТЕРНОЙ ВЫЧИСЛИТЕЛЬНОЙ СИСТЕМЫ

Кокоц А. В.

В настоящее время вычислительные системы кластерного типа получают все большее распространение. Это обусловлено различными факторами, главным из которых является насущная потребность в решении актуальных задач фундаментальной и прикладной науки, для анализа и исследования которых производительности существующих средств вычислительной техники оказывается недостаточно.

Фундаментальные научные или инженерные задачи с широкой областью применения, можно эффективно решить только с использованием мощных (суперкомпьютерных) вычислительных ресурсов.

Вот лишь некоторые области, где возникают задачи подобного рода [1]: предсказания погоды, климата и глобальных изменений в атмосфере, гидро- и газодинамика, науки о материалах, разведка нефти и газа, управляемый термоядерный синтез, генетика человека и многие другие области.

С аппаратной точки зрения кластер представляет собой набор серийно выпускаемых ЭВМ (вычислительных узлов), объединенных сетью передачи данных. С точки зрения программного обеспечения кластер является единой виртуальной машиной, имеющей несколько процессоров и распределенную память. Производительность кластера определяется производительностью его узлов и характеристиками среды передачи данных.

Рост популярности кластерных решений в научной и академической среде привел к появлению практически в каждом ВУЗе страны набора кластеров, как высокопроизводительных для научных расчетов, так и относительно низкопроизводительных для обучения студентов и отладки программ.

Однако при развертывании систем такого рода возникает ряд проблем. Заметное место в этом ряду занимает проблема эффективного управления кластерными системами. Для того чтобы распределенная вычислительная система успешно функционировала, необходимо, по крайней мере, реализовать систему распределения задач по доступным вычислительным ресурсам (систему доступа), обеспечивающую планирование выполнения задач на кластерах (диспетчер заданий) и мониторинг состояния вычислительных ресурсов [2]. В случае отсутствия систем такого рода возможны конфликты в процессе запроса вычислительных мощностей во время проведения экспериментов, что приведет к падению общей производительности системы. Таким образом, разработка программных систем, решающих эти задачи, является необходимым условием успешного развития вычислительных систем рассматриваемого класса.

Многие организации, а особенно университеты, имеют несколько компьютерных классов, на базе каждого из которых легко может быть организован однородный кластер. Так, например, в НИУ МЭИ организована высокопроизводительная вычислительная система (кластер), позволяющая осуществлять свыше 280 млрд. операций в секунду [3]. Территориально кластер расположен в машинном зале ИВЦ МЭИ, но доступ к нему возможен и через компьютерную сеть университета. Пользователями кластера могут быть не только научные работники, но и студенты (аспиранты) и преподаватели МЭИ.

Проблемы параллельных вычислений

Основы  параллельных вычислений отлично раскрыты в работе  Воеводина В. В., Воеводина Вл. В., «Параллельные вычисления».[1]  Начинается все с простых компьютеров: как устроен компьютер; как проводятся операции с числами; как устроена память; какие языки программирования используются. В дальнейшем идет переход к вопросу о том, как улучшить производительность компьютера, что приводит нас к архитектуре параллельных вычислительных систем. Такая логическая последовательность дает читателю хорошие основы в параллельных вычислениях, которые подняты в этой книге и применяются в данном курсовом проекте. Компьютеры постоянно совершенствуют, появляются новые области их применения, требуется повышение их производительности. Из всех способов увеличения производительности, использование параллельных вычислений, занимает далеко не последнее место. Уже сегодня существуют установки, объединяющие тысячи вычислительных узлов в рамках одной коммуникационной сети. К примеру, интернет можно рассматривать как самый большой параллельный компьютер с распределенной памятью, объединяющий миллионы вычислительных узлов. Но как убрать большие накладные расходы, идущие на взаимодействие параллельно работающих процессоров? Как упростить разработку параллельных программ? Как такие системы использовать эффективно? Все эти вопросы авторов, говорят о сложности управления такими системами и их проектирование,  и моделирование таких систем играет важную роль.

Как уже было сказано выше, правильное управление параллельными системами дает высокую производительность. Этого можно добиться составив эффективное расписание для планировщика. Но как составить эффективное расписание? Как оценить эффективность? Такими вопросами задаются в книге Конвея Р.В., Максвелла В.Л., Миллера Л.В. «Теория расписаний». Книга разбита на две части: для конечных работ и не конечных (системы массового обслуживания).  Большую важность в данном курсовом проекте составили эвристические  методы из первой части книги. Авторы подробно разбирают различные способы составления расписаний и их оценки. Методы из этой книги можно применять не только в параллельных вычислениях и во многих других дисциплинах. К примеру при разработке стратегии назначения, можно частично заимствовать идею авторов для организации производства, когда вещи которые требовали не много временных затрат на изготовление, производили вдали от склада. Можно сказать, что разрабатываемая стратегия назначения имеет актуальную роль и может применяться во многих других областях, не связанных с параллельными вычислениями.

Для моделирования кластера нужно задать структуру. Какие принципы построения кластера? Какого его устройство? Какие тенденции развития устройств кластера? Какие возникают сложности? Об этом можно узнать из работы Ладыгина И.И., Логинова А.В., Филатова А.В., Янькова С.Г.  «Кластеры на многоядерных процессорах». В книге уделено огромное внимание кластеру НИУ МЭИ, поэтому можно взять структуру кластера схожего с кластером НИУ МЭИ. Некоторые детали можно упростить для наглядности, также у пользователей будет возможность легко произвести модификацию под кластер другой структуры. Подробно описано устройство узлов, с использованием современных процессоров фирмы AMD, а также технологией AMD HyperTransport, позволяющей быстро производить передачу данных между процессорами в узле. Способы обмена данных между узлами, с помощью технологии Infiniband, возможность связи узлов с внешним миром, используя Gigabit Ethernet. Распределение памяти по узлам, подробное описание процессора AMD и обмен данных между ядрами в нем, все это тоже можно узнать их этой книги.

Для моделирования кластера нужно выбрать задачу, с практическим применением, для которой мы хотим провести моделирование. Какие задачи можно решать, используя параллельные вычисления? Какая должна быть структура задачи? Какие задачи эффективно решать, с использование параллельных вычислений? С практическим применением параллельных вычислений можно подробно столкнуться в книге Гергель В. П. «Теория и практика параллельных вычислений». В наше время, практических во многих  прикладных задачах приходится иметь дело с системами линейных алгебраических уравнений (СЛАУ). Множество сложных задач, к примеру, решение дифференциальных уравнений, можно свести к СЛАУ. Некоторые СЛАУ могут иметь огромную размерность и без использования параллельных вычислений могут быть не решены, к примеру, при решении в отведенное время. Автор обращает внимание читателя на важность примеров решение СЛАУ, очень подробно разбирает эффективность, ускорение, сложность, возможности распараллеливания, а также результат экспериментов. К примеру, автор приводит таблицу эксперимента, в которой ускорение при решении СЛАУ, всем известного метода Гаусса, приблизительно равно 5-ти, с использованием 8-ми процессоров и размерностью системы 3000. Стоит отметить, что при малой размерности и большом количестве процессоров ускорение становится меньше единицы, что указывает о неэффективности применения параллельных вычислений, в таких ситуациях. В книге разобрано еще множество методов для решения различных прикладных задач, что говорит о широких возможностях применения параллельных вычислений. Руководствуясь данной книгой можно подобрать задачу, которую позволяла пользователю моделировать решение СЛАУ.

Также стоит отметить документацию Parallel Computing Toolbox™ User’s Guide R2013b, которая позволяет пользователям мощного продукта MATLAB решать тяжелые математические задачи на многоядерных компьютерах, кластерах, графических ускорителях. Кроме решения, позволяет проводить моделирование с использованием Simulink, что заметно ускоряет работу со сложными моделями. Большое внимание уделено обмену данных при параллельных вычислениях, командам parfor (цикл for разбивается на части и выполняется параллельно на вычислителях) и smdp (позволяет выполнить блок кода параллельно на вычислителях). Огромную работу пользователя, забирает на себя планировщик, что позволяет использовать продукт легко. Читая документацию, можно увидеть моменты приоткрывающие работу планировщика, и применить их в курсовой. К примеру имитационное моделирование по событиям. Ко всем плюсам у продукта есть и минусы, одним из самых главных минусов это ограничение на количество вычислителей, прозрачность кода, невозможность задавать количество for-loops функцией и т. д. Для некоторых людей цена продукта, тоже может быть существенным недостатком. Постоянные обновления, высокая цена продукта, говорят о важности применения параллельных вычислений.

На сайте  www.parallel.ru можно всегда узнать последние новости в области параллельных вычислений. Всю информацию о новых достижениях, предстоящих мероприятиях, областях применения можно узнать, зайдя на сайт. Также на сайте присутствует форум, с более чем 4000 тем, что позволяет общаться на темы связанные с параллельными вычислениями. Кроме того на сайте имеется новостная подписка. С данного сайта можно использовать информацию о последних применениях параллельных вычислений.

Для написания программы нужен удобный, понятный, привлекательный интерфейс.  Многие пользователи могут отказаться работать с продуктом, имеющим плохой интерфейс.  Так как среда разработки Microsoft Visual Studio Community 2015 и язык C#, то книга Гербердта Шилдта  «С# 4.0 Полное руководство», является незаменимым справочником для людей, которые работают с .Net технологиями. Исходя из этой книги, выбор технологии создания интерфейса нужно сделать из Silverlight, XAML, WPF и Windows Form. Для данной курсовой работы практичнее будет выбрать использование Windows Form,  так как интерфейс простой, а также программа с использованием этой технологии будет работать на компьютерах c ОС, начиная с XP. Минусы Windows Form будут заключаться в трудоемкости портирования на другие устройства, данной программы, а также в сложности создания динамических интерфейсов.

Из всех приведенных выше источников, можно сделать вывод о высокой ценности параллельных вычислительных систем с использованием кластера и необходимости их моделирования. Многие авторы, во всех приведенных источниках частично касаются данной проблемы, но нигде она не доведена до конца.

Анализ предметной области

Вычислительный кластер есть совокупность вычислительных узлов, объединенных с помощью специальной коммуникационной среды и представляющий собой единый вычислительный ресурс для решения одной сложной задачи или набора независимых задач [3]. В качестве коммуникационной среды выступает иерархия коммутаторов, обеспечивающих взаимодействие ядер внутри узла кластера, взаимодействие узлов и взаимодействие кластера с внешним миром. Каждый узел в кластере работает под управлением своей копии операционной системы (ОС), в качестве которой чаще всего выступают: Linux, Windows NT, Solaris и др [4]. Существенной особенностью кластеров, является применение, в качестве всех его компонент, серийно выпускаемых производителями средств вычислительной техники. Состав, число и мощность узлов может меняться даже в рамках одного кластера, что дает возможность создавать неоднородные системы с возможностью дальнейшего расширения (масштабирования). Выбор конкретной коммуникационной среды определяется многими факторами: особенностями класса решаемых задач, ограничениями по финансированию, необходимостью последующего расширения. В состав кластера, как правило, входит так называемый управляющий узел, задачами которого является выполнение функций распределения ресурсов под задачи пользователя, управление параллельным выполнением программ, отображением результатов вычислений, связи с внешним по отношению к кластеру миром. В состав кластера может быть введен и специализированный узел, например файл-сервер [3]. Поскольку системы данного класса относятся к системам с распределенной памятью, то взаимодействие вычислительных узлов между собой осуществляется с помощью передачи сообщений. При этом аппаратно-программные реализации технологии коммуникаций, исходя из соображений стоимости и производительности, могут быть простыми, например основанными на аппаратуре Ethernet, или сложными с высокоскоростными сетями с пропускной способностью в сотни мегабайт в секунду, например InfiniBand.

Идея построения вычислительных систем с распределенной памятью очень проста. Берется какое-то количество вычислительных узлов, которые объединяются друг с другом некоторой коммуникационной средой. Каждый вычислительный узел имеет один или несколько процессоров и свою собственную локальную память, разделяемую этими процессорами. Распределенность памяти означает то, что каждый процессор имеет непосредственный доступ только к локальной памяти своего узла [5]. Доступ к данным, расположенным в памяти других узлов, выполняется дольше и другими, более сложными способами.

В настоящей работе будем использовать упрощенную топологию кластера МЭИ (Рис. 2.1). Кластер состоит из 16 вычислительных узлов СN_i, которые соединены коммуникационной средой SW₂. В каждом вычислительном узле два процессора PM_i, процессоры соединены между собой коммуникационной средой SW₁, в свою очередь SW₁ связана с SW₂. На каждый процессор приходится два ядра (производительность ядер одинакова), соединенных коммуникационной средой SW₀, SW₀ подсоединена к SW₁.  Каждая коммутационная среда имеет свою пропускную способность C₀, C₁, C₂ соответственно.

Стоит также отметить важную роль распределенной памяти в данной структуре, к примеру обмен данных между ядрами, через SW₀  осуществляется через кэш 2-го уровня, при этом одно ядро не может получить доступ к кэш памяти 1-го уровня другого ядра и наоборот. Аналогичная ситуация и с SW₁ , каждый узел можно представить как отдельную вычислительную машину, с оперативной памятью, доступ к которой имеют процессоры, находящиеся в одном узле с ней.

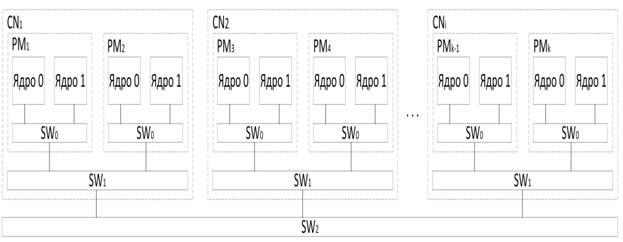
Рис. 1 Топология кластера

Средства решения поставленной задачи

Существенным фактором, влияющим на процесс эффективного исполнения прикладной программы на кластере, является выбор и организация работы операционной системы. Основными функциями такой ос могут быть: Распределение ресурсов многомашинной вычислительной системы (ММВС) для множества задач, выполняемых ею (эту функцию выполняет так называемый планировщик); синхронизация параллельных процессов; организация обмена сообщениями и др [3].

В теории параллельного программирования существует понятие ярусно-параллельной формы (ЯПФ) представления программы [4]. В этом случае программа представляется как последовательность ярусов. На каждом ярусе размещаются операторы программы, которые могут выполняться одновременно друг с другом, то есть параллельно. На каждом последующем ярусе располагаются операторы, которые могут быть выполнены только после операторов предыдущего яруса. Схематически ярусно-параллельную форму программы можно представить в виде графа. Операторы программы являются вершинами графа (показаны овалами), а дуги - это зависимости операторов друг от друга.

Теоретической основой решения задачи назначения является теория расписаний [4]. Под решением задачи назначения понимается процесс распределения вершин графа задачи (набора задач), выполняемой в ММВС, между ее процессорами, при котором определяется время начала выполнения вершины, его длительность и назначение процессора, который обеспечит это выполнение. Модель процесса распределения включает средства, описывающие ресурсы, систему вершин и дуг графа задачи (набора задач) и критерий оптимальности распределения. Под ресурсами понимаются: модули обработки (процессоры), модули памяти (она может быть распределенной, общей или смешанной), внутрисистемный интерфейс (общая шина, мультиплексная шина). При построении алгоритмов назначения в отказоустойчивых ММВС в модель должны быть введены средства, описывающие систему обеспечения отказоустойчивости ММВС. Например, средства, обеспечивающие введение дополнительных копий вершин графа задачи и дополнительных процессоров.

В качестве критериев оптимальности распределения вершин в ММВС применяются обычно либо минимум времени выполнения задачи (набора задач) при ограничении на число процессоров, либо минимум числа требуемых процессоров при ограничении на время решения задачи (набора задач).

В качестве производных от этих критериев используются следующие – коэффициент загрузки каждого процессора (К _{загр i})

К _{загр i}  = Т_i / Т_вып ,

где Т_i – время, в течение которого i-й процессор занят обработкой задачи, Т_вып - время выполнения задачи [6]. Зная коэффициенты загрузки процессоров можно найти средний коэффициент загрузки (К _{загр ср})

К _{загр ср} =  ,

где - коэффициент загрузки i-го процессора, n – кол-во процессоров. Следует отметить при этом, что эффективность как алгоритма распределения вершин задачи, так и выбранной структуры ММВС можно оценить с помощью коэффициента ускорения (К _уск), показывающего ускорение времени решения задачи на n процессорах в сравнении с временем решения этой же задачи на одном процессоре

К_уск =  T_max / Т(n) ,

где T_max - время решения задачи на одном процессоре, Т(n) - время решения задачи на n процессорах [6].

В теоретическом плане при построении алгоритмов оптимальных расписаний могут быть использованы математические методы, например, динамического программирования. Однако это достаточно сложная проблема, так как необходимо решать задачи большой размерности, при этом они относятся к NP – полным [4]. На практике оптимальные расписания с использованием таких методов построены для простых типов прикладных задач сравнительно небольшой размерности, причем в основном для двухпроцессорных систем. Поэтому обычно применяются методы приближенной оптимизации, в частности, эвристические методы. Эвристические методы построения расписаний характеризуется тем, что они приспосабливаются  структурной организации ММВС, и относятся к классу приоритетного распределения. В таких расписаниях вершинам задачи присваивается приоритет по тем или иным правилам (стратегия назначения), после чего вершины упорядочиваются в виде линейного списка по убыванию приоритетов. В процессе составления расписания осуществляется назначение вершин на процессоры в соответствие с их приоритетами для их выполнения. Наиболее исследованы и представлены в литературе различными моделями следующие стратегии назначении готовых к выполнению вершин вычислительного процессах [4]:

1) равновероятностный выбор;

2) выбор вершины с минимальным временем выполнения;

3) выбор вершины с максимальным временем выполнения; 

4) выбор вершины, принадлежащей критическому пути;

5) выбор вершины, имеющей наибольшее число связей с последующими вершинами;

6) выбор вершины в порядке поступления в очередь в порядке исполнения.

В настоящей работе задачи представляются в виде графа ЯПФ, с взвешенными вершинами: время выполнения t_i; объем данных v_i. Время выполнения вершины может быть рассчитано пользователем из производительности ядра и количества операций.  Вершина последователь должна получить все данные от вершин предшественников, объемом  v_i, заданным у каждой вершины предшественников.  Ребра графа будут взвешиваться временем передач, полученным из v_i и С_i, исходя из такого, какой будет путь передачи данных.

Также, при вводе t_i , v_i , С_i значений, единицы измерения должны соответствовать друг другу, к примеру, если все t_i заданы в секундах, а все v_i в байтах, тогда все С_i должны быть заданны в байт на секунду, а Т_вып будет в секундах. В дальнейшем, вместо вершин могут использоваться задачи – имеют те же параметры что и вершины, а также содержат информацию о том, какое ядро выполнило задачу (вершину), когда начало выполнять и закончило.

Стратегия назначения заключается в том, что вершины  с большим временем выполнения назначаются на ядра, которые ближе к первому ядру, c меньшим – дальше. Такая стратегия позволит сделать Т_вып как можно меньше.

Модель моделирования будет имитационной по событиям, при этом событием является ближайшее время освобождения ядра.

Перечень решаемых задач

1) Реализация удобного для пользователя интерфейса, с возможностью создания, редактирования, открытия, сохранения графа задач. Пользователь должен иметь возможность установить параметры кластера и получить информационное окно, подробно содержащее все результаты моделирования. Интерфейс должен содержать оповещения пользователя об неправильно введенных данных, ошибках.

2) Использовать для ввода и вывода данных о графе XML формат, что позволит пользователю с легкостью просмотреть, изменить граф задач, вдобавок к конструктору графа в самой программе [7].

3) Разработка алгоритма стратегии назначения.

Разработка структуры программы

Структура программы представлена в виде ULM диаграммы классов (Рис. 2, 3).

На первой диаграмме находится класс Graph, который содержит все данные о ЯПФ графе. Класс Cluster содержит данные кластера и главный метод  LocalSimulate, по стратегии назначения. В Cluster используются классы Task и Core. Класс Task, содержит в себе информацию вершины из графа, а также данные для информационного окна. Класс Core содержит информацию о времени освобождения ядра, а также информацию о хранящихся данных с выполненных задач. Класс Program, главный класс который содержит главное окно.

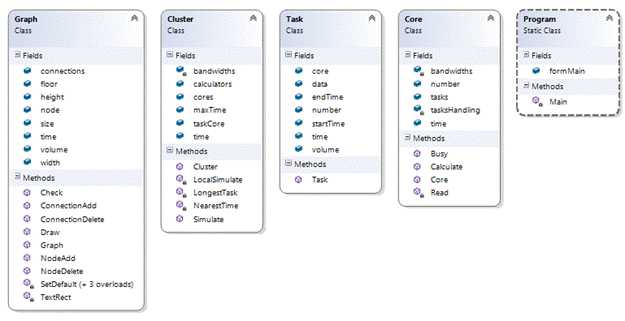
Рис. 2. ULM диаграммы классов 1

На второй диаграмме присутствуют два класса по умолчанию Settings, Resources. Класс FormMain является главным окном, в котором рисуется граф, находится меню. Также содержит в себе объекты графа и кластера и методы XML сохранения и чтения. Классы FormNewGraph и FormNodeAdd представляют собой часть окон конструктора графа.

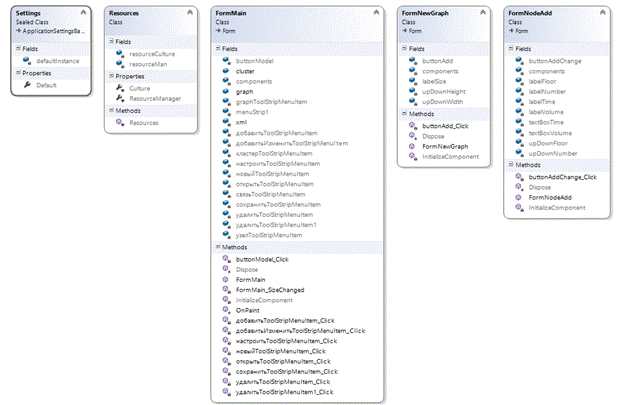
Рис. 3. ULM диаграммы классов 2

На третьей диаграмме, классы FormConnectionAdd, FormNodeDelete, FormConnectionDelete, также являются частью окон конструктора графа. Класс FormClusterSetup представляет собой окно для установки параметров кластера. Класс FormResults – информационное окно выводящее результаты моделирования на экран.

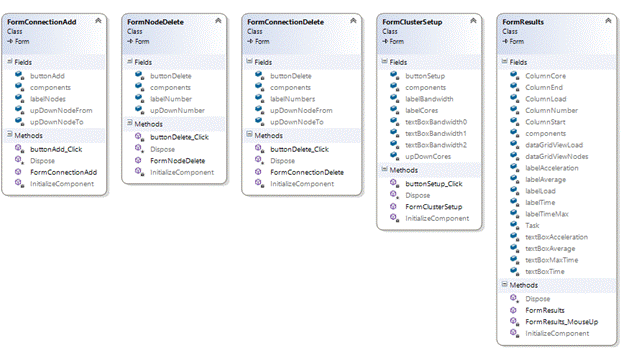
Рис. 4. ULM диаграммы классов 3

Разработка и описание рабочих алгоритмов

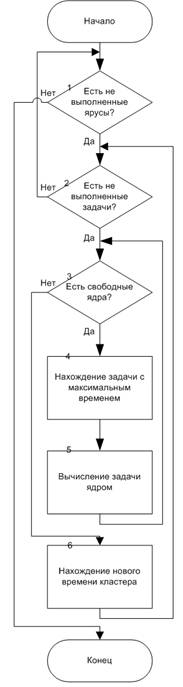
Главный интерес представляет алгоритм метода LocalSimulate, класса Cluster, по стратегии назначения (Рис 5,6):

1) Идем по ярусам сверху вниз, в случае наличия яруса к шагу 2, иначе конец;

2) Проверяем, остались ли задачи в списке задач яруса, если задач нет, то идет дополнительная проверка, выполняют ли ядра задачи в текущее время кластера, если ядра не работают, то шаг 1, иначе шаг 3;

3) Идем по ядрам от первого к последнему, что позволит нам загружать ядра как можно ближе к первому. Проверяем, наличие свободных ядер в текущее время кластера, если есть, то шаг 4, нет - шаг 6;

4) Среди списка задач яруса находим задачу с максимальным временем выполнения, передаем её в шаг 5;

5) Найдена задача в шаге 4, передается методу Calculate (разобран дальше)  класса Core, к шагу 6.

6) Новое текущее время кластера находится как минимальное время из времен освобождения ядер, но при этом больше текущего времени кластера, переход к шагу 3.

Рис. 5. Схема алгоритма метода LocalSimulate

_____

Рис. 6. Схема алгоритма метода Calculate

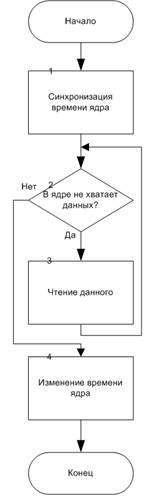
Рис. 7. Схема алгоритма метода Read

Метод Calculate, класса Core, используется методом LocalSimulate (Рис 6):

1) Текущие время кластера присваивается времени освобождения ядра, также задача удаляется из списка задач для яруса, переход к шагу 2;

2) Проверяем,  наличие всех данных задач предшественников необходимых для выполнения текущей задачи, если нет данного, то шаг 3, иначе шаг 4;

3) Задача, данных которой нет в ядре, из шаге 2, передается методу Read (разобран дальше)  класса Core, переход к шагу 4.

4) Время освобождения ядра заносится как время начала выполнения задачи, затем к времени освобождения ядра прибавляется время необходимое для выполнения текущей задачи и запоминается как время окончания выполнения. Кроме того запоминается номер задачи и номер ядра, которое выполнило её, переход к концу.

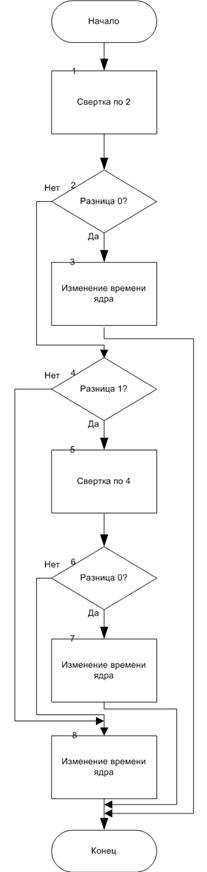
Метод Read, класса Core, используется методом Calculate (Рис 7):

1) Устанавливаем первый номер ядра – номер ядра которое выполняет метод Calculate, второй номер ядра (для чтения) устанавливаем по списку соответствия задача – процессор, который её выполнил. Целочисленно делим номера ядер на 2, с округлением в меньшую сторону, затем вычитаем и берем модуль, для нахождения разницы, переход к шагу 2.

2) Если разница 0, то ядра в одном процессоре, шаг 3, иначе шаг 4;

3) К времени освобождения ядра, которое выполняет метод Calculate, прибавляем время передачи через SW₀ (объем данных, задачи которую считываем, умножаем на  1/С₀). Запоминаем, что данные теперь есть и в ядре, которое производило чтение, переход к концу.

4) Если разница 1, то нужна дополнительная проверка, шаг 6, иначе ядра в разных узлах, шаг 8.

5) Устанавливаем первый номер ядра – номер ядра которое выполняет метод Calculate, второй номер ядра (для чтения) устанавливаем по списку соответствия задача – процессор, который её выполнил. Целочисленно делим номера ядер на 4, с округлением в меньшую сторону, затем вычитаем и берем модуль, для нахождения разницы, переход к шагу 6.

6) Если разница 0, то ядра в одном узле, в разных процессорах, шаг 7, иначе в разных узлах, шаг 8.

7) К времени освобождения ядра, которое выполняет метод Calculate, прибавляем время передачи через два SW₀ и один SW₁ (объем данных, задачи которую считываем, умножаем на сумму из 1/(2С₀) и 1/С₁). Запоминаем, что данные теперь есть и в ядре, которое производило чтение, переход к концу.

8) К времени освобождения ядра, которое выполняет метод Calculate, прибавляем время передачи через два SW₀ , два SW₁ и один SW₂ (объем данных, задачи которую считываем, умножаем на сумму из 1/(2С0₀), 1/(2С₁) и 1/С₂). Запоминаем, что данные теперь есть и в ядре, которое производило чтение, переход к концу.

Алгоритм нахождения основных результатов моделирования для информационного окна (Рис 8):

1) Запускаем метод моделирования LocalSimulate, для одного ядра, получаем T_max, переход к шагу 2.

2) Если ядро в кластере одно, то Т_вып присваиваем T_max и переходим на  шаг 4, иначе шаг 3;

3) Запускаем метод моделирования LocalSimulate, получаем Т_вып , переход к шагу 4.

4) Находим коэффициент ускорения (T_max / Т_вып), к шагу 5.

5) Идем по всем задачам, для считывания результатов моделирования, если все задачи прошли, шаг 7, иначе 6.

6) По задаче в шаге 5, находим ядро, на котором она выполнялась, увеличиваем время работы ядра на время выполнения задачи, переход к шагу 4.

7) Идем по всем ядрам,  для нахождения коэффициентов загрузок, если все ядра прошли, шаг 9, иначе 8.

8) Находим для ядра К_загр (время работы ядра делим на Т_вып), кроме того прибавляем найденный коэффициент к сумме коэффициентов загрузок, затем переход к шагу 7.

9) Находим К_{загр ср} (сумму коэффициентов загрузок делим на их количество), переход к концу.

Разработка интерфейса взаимодействия с системой

При запуске программы открывается  главное окно программы (Рис. 8), размер окна можно менять, в соответствии с изменением окна меняется размер графа, который рисуется в нем. Левая цифра над вершиной – время выполнения, правая – объем данных.

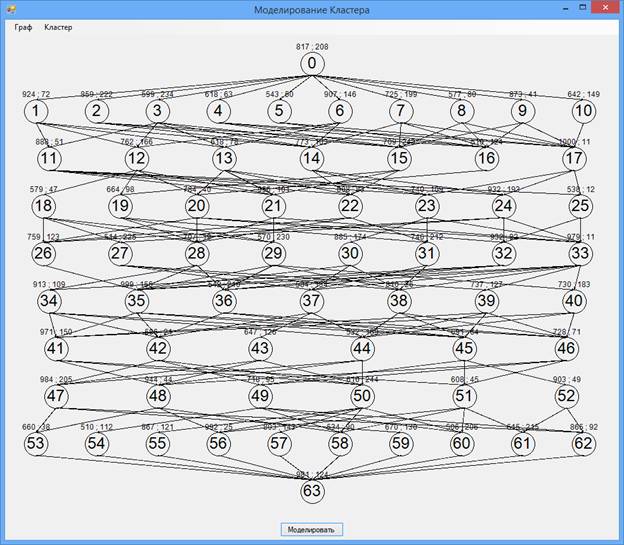
Рис. 8. Главное окно программы

Меню содержит подменю «Граф», с помощью которого мы можем вызвать стандартные окна открытия, сохранения, для графа. Также можем вызвать окно создания нового графа указав в нем максимальный размер графа (слева на право для ширины, высоты).

Подменю «Граф» содержит подменю «Вершина», в нем мы можем открыть добавления новой вершины и задать в нем номер вершины, ярус, время выполнения и объем данных.

В подменю «Вершины» присутствует возможность открыть окно удаления вершины, в нем устанавливается номер вершины который мы хотим удалить.

В подменю «Граф», кроме подменю «Вершина», находится подменю «Связь». С его помощью можно открыть окно добавления связи и указать номера двух вершин которые мы хотим соединить.

Также в подменю «Связь», можно открыть окно удаления связи и указать номера двух вершин, связь между которыми мы хотим удалить.

Кроме  подменю «Граф», в главном меню, есть подменю «Кластер», которое позволяет нам открыть окно настройки кластера в нем устанавливается количество ядер, а также пропускные способности  коммуникационных сред (Сверху вниз для SW₀, SW₁ , SW₂).

 «Моделировать», запускается моделирование и открывается окно результатов моделирования (Рис. 9). Окно результатов моделирования содержит всю необходимую информацию о результатах моделирования.

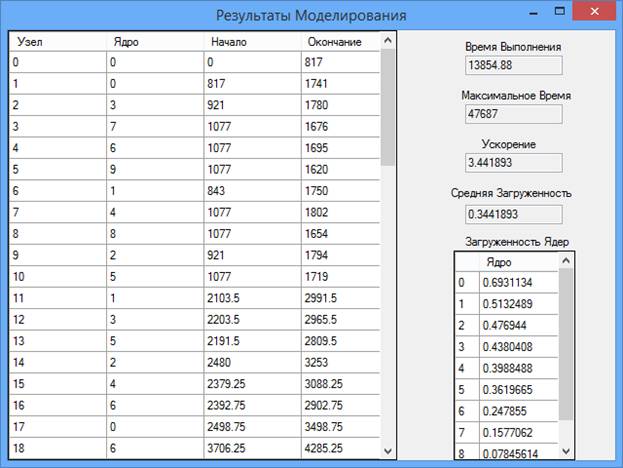
Рис.9. Окно результатов моделирования

В программе присутствуют окна оповещения пользователя об удачной выполненной операции или неправильно введенных данных.

Тестирование программных средств

Программа разработана на языке высокого уровня C#, откомпилирована и отлажена в Microsoft Visual Studio Community 2015.

Цель тестирования проверить работоспособность программы, тестирование проводилось на ЭВМ со следующими параметрами: Процессор Intel core i5-3230M, ОЗУDDR3 4GB, ОС Windows 10 64x Professional.

Программа отлавливает все исключительные ситуации и оповещает пользователя об этом, указывая, что пользователь должен сделать. Примеры исключительных ситуаций: запуск  моделирования без графа или без настроенного кластера; ввод отрицательных чисел или чисел не в правильном формате, диапазоне; открытие поврежденного файла с графом или файла неправильного формат; добавление вершины которая уже существует или удаление вершины которого нет;  добавление связи которая уже есть или удаление связи которой нет; добавление связи вершин не с соседних ярусов и т. д.

Инструкция пользователя

Для работы программ необходимы минимальные требования для клиентских ОС Windows XP и выше, для серверных ОС Windows Server 2003 и выше, процессор IntelPentium II, 233MHz, место на диске 4MB, клавиатура, мышь.

Установка производится копированием  всех установочных файлов в любую директорию на компьютере. Интерфейс программы предельно прост и не требует никаких специальных навыков.

Работа с программой осуществляется запуском файла с расширением *.exe, созданием или открытием графа, настройкой параметров кластера и после этого запуском моделирования. Выход из программы аналогичен закрытию она Windows.

Моделирование

Моделирование будет проводить со слабосвязанным графом (Рис. 10) (время передачи данных меньше времени выполнения вершины) и сильно связанным (Рис. 14)  (время передачи данных больше времени выполнения вершины). Максимальная размерность графов 10 на 10. Различаются графы только объемами данных при вершинах. В обоих случаях пропускные способности кластера одинаковые, будем менять количество ядер, чтобы получить их зависимости от времени выполнения, коэффициента ускорения и среднего коэффициента загрузки ядер, чтобы оценить разработанную стратегию назначения вершин.

По результатам моделирования (Таблица 1) слабосвязанного графа и построенным по ним зависимостям (Рис. 11 - 13), можно сделать вывод, что увеличение числа ядер до 4х дает существенный прирост ускорения (соответственно уменьшение времени выполнения). Дальнейшее увеличение числа ядер приводит к тому, что ядра простаивают на ярусах где вершин меньше чем ядер, вдобавок увеличивается количество пересылок данных между ядер, соответственно прирост ускорения замедляется. Увеличить прирост ускорения можно с помощью увеличения пропускных способностей.

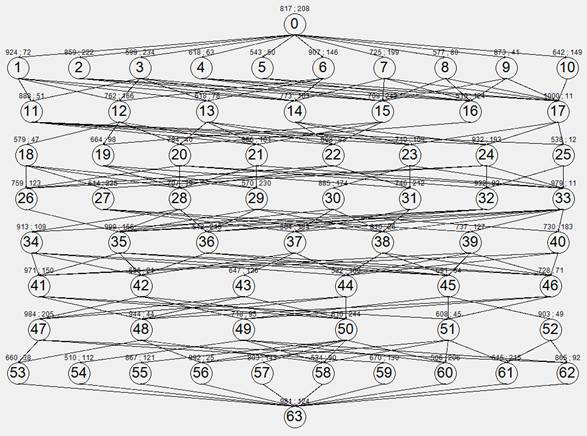
Рис. 10. Слабосвязанный граф

Таблица 1

Результаты моделирования слабосвязанного графа

Кол-во ядер	1	2	3	4	5	6	7	8	9	10
Tвып	47687	25793.75	20056.13	16481.38	16502.75	15099.13	14880.25	14305.88	14387.13	13854.88
Куск	1	1.848781	2.377678	2.893387	2.88964	3.158262	3.204718	3.333386	3.314561	3.441893
Кзагр ср	1	0.9243906	0.7925592	0.7233468	0.5779279	0.5263771	0.4578168	0.4166732	0.3682845	0.3441893

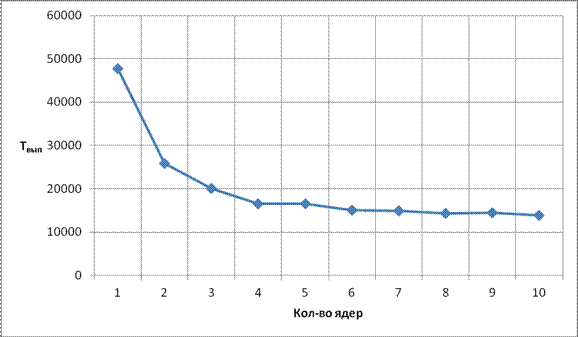
Рис. 11 Зависимость T_вып от кол-ва ядер для слабосвязанного графа

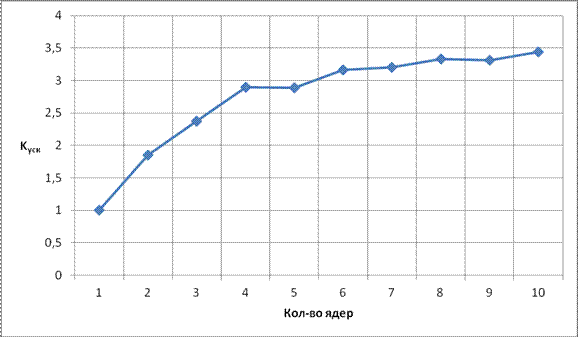
Рис. 12. Зависимость K_уск  от кол-ва ядер для слабосвязанного графа

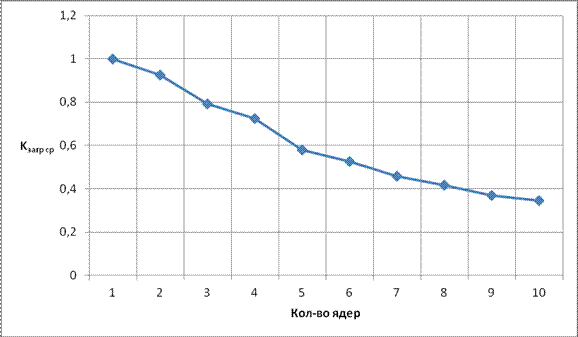
Рис. 13 Зависимость от K_{загр ср}  от кол-ва ядер для слабосвязанного графа

Из результатов моделирования (Таблица 2) сильновязанного графа и построенным по ним зависимостям (Рис. 5.6 – 5 .8), можно сделать вывод, что увеличение числа ядер до 2-х дает существенный прирост ускорения (соответственно уменьшение времени выполнения), от 2-х до 4-х можно сказать, что прирост сравним с нулем. Дальнейшее увеличение числа ядер приводит к тому, что ядра простаивают на ярусах где вершин меньше чем ядер, вдобавок увеличивается количество пересылок данных между ядер, что является существенным фактором, делающий прирост ускорения отрицательным, в итоге результаты при 10-ти ядрах хуже, чем при 1-ом ядро. Сильно увеличить прирост ускорения можно с помощью увеличения пропускных способностей.

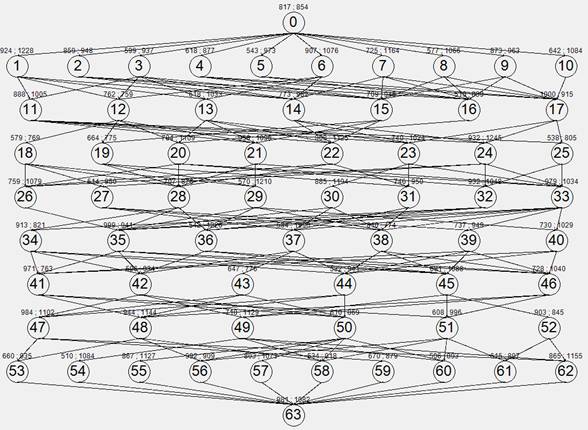
Рис. 14. Сильно связанный граф

Таблица 2

Результаты моделирования сильносвязанного графа

Кол-во ядер	1	2	3	4	5	6	7	8	9	10
Tвып	47687	29110.5	31931.5	29490.38	43079.38	44257.75	43789.88	44420.13	46010.5	47809.88
Куск	1	1.638137	1.493416	1.617036	1.106957	1.077484	1.088996	1.073545	1.036437	0.9974299
Кзагр ср	1	0.8190687	0.4978052	0.404259	0.2213914	0.1795806	0.1555709	0.1341931	0.1151597	0.09974299

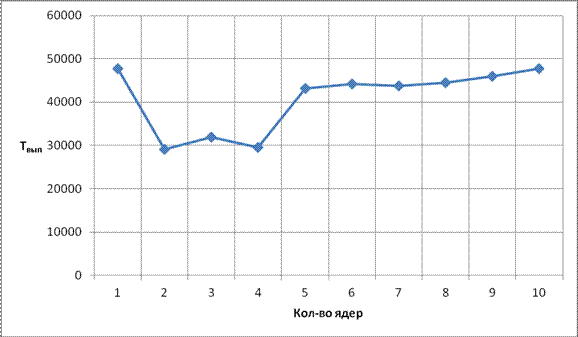
Рис. 15 Зависимость T_вып от кол-ва ядер для сильно связанного графа

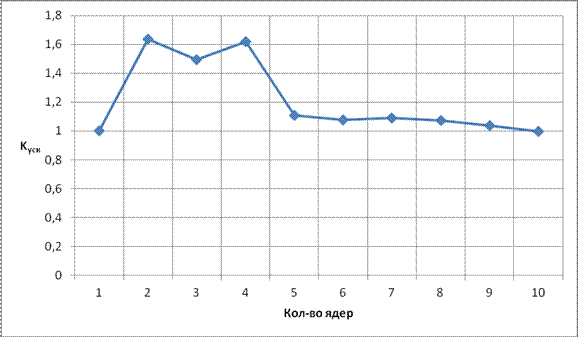
Рис. 16 Зависимость K_уск  от кол-ва ядер для сильно связанного графа

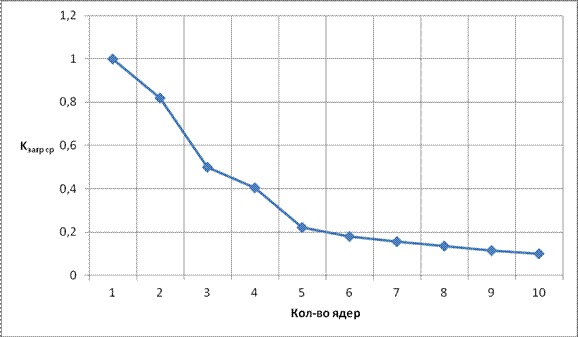
Рис. 5.8 Зависимость K_{загр ср} от кол-ва ядер для сильно связанного графа

Разработанный алгоритм эффективно использовать для слабосвязанных задач, слабым местом алгоритма являются задачи другого типа с большим количеством ядер.

Заключение

В процессе выполнения работы были рассмотрены основы кластерных систем, планировщиков, графовых задач, стратегий назначений, топология кластера МЭИ. Была разработана программа моделирующая работу кластера с топологией кластера МЭИ, со стратегией назначения вершин, возможностью создавать, сохранять, открывать графовую задачу, задавать пользовательские характеристики кластера.

На основе разработанной программы были произведены исследования разработанной стратегии назначения вершин, а также выявлены слабые места и эффективные области применения. Получены зависимости времени выполнения, коэффициента ускорения, среднего коэффициента загрузки ядер от количества ядер. Зависимости получены для двух видов графовых задач: слабосвязанных и сильно связанных.

Данная программа может применяться для решения СЛАУ и дифференциальных уравнений, благодаря возможности изменять граф задач.

Так как пользователь может изменять параметры кластера, то возможно моделирование других кластеров со схожей топологией. Программа легко поддается модификации, и в дальнейшем, есть возможность добавления учета памяти при моделированию. Программа может работать на большом количестве компьютерах, а также на компьютерах со старыми ОС. Имеется простой, привлекательный, интуитивный интерфейс, что не вызовет у пользователя отвращения или непониманию. Время разработки и отладки заняло 2 месяца, общий объем кода программы составил 1300 строк на языке С#.

Литература

1. Материалы сайта www.parallel.ru

2. Parallel Computing Toolbox™ User’s Guide R2013b

3. И.И.Ладыгин, А.В.Логинов, А.В.Филатов, С.Г.Яньков Кластеры на многоядерных процессорах . – М: Издательский дом МЭИ , 2008. – 112 с.

4. Конвей Р.В., Максвелл В.Л., Миллер Л.В. Теория расписаний. М.: Наука, 1975. - 360 с.

5. Воеводин В. В., Воеводин Вл. В., Параллельные вычисления - СПб: БХВ-Петербург, 2002. – 608 с.

6. Гергель В. П., Теория и практика параллельных вычислений - М.: БИНОМ. Лаборатория знаний, 2007. – 424 с.

7. Гербердт Шилдт  С# 4.0 Полное руководство  Т.1. – Вильямс, 2011. 1056 с.