BC/NW 2016 № 2 (29):7.1
РАЗРАБОТКА ПОТОКОВОЙ МОДЕЛИ VPN
Симонов Д.А.
Благодаря стремительному развитию процесса глобализации, компании и корпорации столкнулись с необходимостью иметь территориально распределенные структурные единицы – филиалы, дочерние компании и т.д. Вдобавок, распространённость сети Интернет позволила корпорациям нанимать лучших работников со всех частей света, которые могут работать удалённо. Однако данные возможности породили целый ряд проблем, касающихся связи между отдельными филиалами компаний между собой и сотрудниками, работающими удалённо. Казалось, что всемирно распространённая сеть Интернет должна решить поставленные проблемы, однако вопрос конфиденциальности корпоративной информации по–прежнему оставался открытым – передавать данные по сетям общего пользования в открытом виде было бы небезопасно. Тогда была предложена идея организации логических сетей поверх обычных (например, Интернет). Ряд реализованных технологий получил название VPN – виртуальные частные сети; это позволило использовать различные средства криптографии для защиты передаваемой информации, а также организовывать сети необходимой конфигурации.
Необходимость в использовании технологий типа VPN поставила перед провайдерами (осуществляющими доступ в Интернет и оказывающими при этом немалый список дополнительных услуг) задачу грамотного проектирования сетей VPN исходя из требований заказчика. Оптимальная структура реализованной сети VPN позволяет провайдеру, с одной стороны, минимизировать затраты на суммарно занимаемую полосу пропускания сети, а с другой – обеспечить заказчику необходимое качество обслуживания (например, отказоустойчивость). Оптимальное решение может быть достигнуто с помощью внешней по отношению к сети системы, в автономном режиме. Система должна включать в себя подсистемы расчетов и имитационного моделирования. Это позволяет учитывать целый ряд параметров, сложно поддающийся анализу в рамках существующих протоколов сетей: интенсивности потоков данных, их пульсации, загрузка ресурсов, задержки, потери. Таким образом, были предложены потоковые модели VPN – графовые модели виртуальных частных сетей, в которых вершины соответствуют пользователям VPN или сетевому оборудованию, а рёбра – каналам связи между ними. В рамках данного курсового проекта будет разработана и протестирована потоковая модель VPN с заданными в ТЗ (приведено в приложении А) характеристиками. В рамках разработанной модели будут сделаны выводы о целесообразности применения выбранного алгоритма построения сети, будет проведено исследование зависимости суммарной занимаемой полосы пропускания сети VPN от количества конечных точек.
АНАЛИЗ ЗАДАНИЯ И ПОСТАНОВКА ЗАДАЧИ
Согласно техническому заданию, необходимо разработать потоковую модель VPN с заданными параметрами: Asym/T/∞/Stat. Исходя из этого, для начала следует определиться с возможными параметрами потоковых моделей VPN:
— равенство входящей и исходящей полосы пропускания;
— тип маршрутизации передачи трафика VPN;
— доступная полоса пропускания на участках сети;
— возможность изменения пропускной способности рёбер VPN со временем.
В книге [2] предложено классифицировать модели в виде символьной формулы A/B/C/D, каждый из символов которой соответствует каждому вышеописанному пункту. Следует рассмотреть данные параметры подробнее.
Трафик,
а, следовательно, и требуемые полосы пропускания на вход и выход из конечной
точки VPN 
, 
, v ∈ Q (Q – множество
вершин графа) может соответствовать следующим случаям:
а)
симметричный трафик (Sym): = ∀ v ∈ Q. Является частным случаем
ассиметричного трафика;
б)
суммарно–симметричный трафик (
): 
;
в)
ассиметричный трафик (Asym) — является общим случаем: и имеют
произвольные значения.
Различные способы маршрутизации передачи трафика вносят дополнительные ограничения решения данной задачи. Маршрутизация делится на 4 вида:
а) древовидная маршрутизация (T). В этом случае совокупность ребер графа, на которых резервируется требуемая полоса пропускания для соединения конечных точек VPN, образует дерево T. Трафик от любой конечной точки до любой другой передается по единственному пути в этом дереве;
б) неразделяемая статическая маршрутизация трафика (NSplit). Для каждой пары конечных точек VPN (u, v) в графе сети G полоса пропускания резервируется на протяжении всего определенного пути Puv. Совокупность ребер VPN образуют подграф G’. Стоит отметить, что обратный путь Pvu может быть не равен Puv по набору входящих в него ребер;
в) разделяемая статическая маршрутизация трафика (Split). Для каждой пары конечных точек VPN (u, v) в графе Q требуемая полоса пропускания может быть разделена между несколькими путями на основании определенного критерия или параметра;
г) разделяемая динамическая маршрутизация трафика (Dyn). Для каждой пары конечных точек VPN (u, v) в графе Q требуемая полоса пропускания может быть разделена между несколькими путями произвольным образом. Отличие от предыдущего способа маршрутизации заключается в том, что при динамической маршрутизации трафика возможно изменение разделения и состава путей с течением времени – классический пример так называемой балансировки нагрузки в сети.
Доступная полоса пропускания на участках сети может принимать два типа значений:
а) бесконечная (∞). Предполагается, что полоса пропускания сети, на базе которой строится VPN, во много раз больше, чем требуемая полоса пропускания на ребре VPN;
б) ограниченная (Fix). Доступная полоса пропускания на ребре ограничена произвольным значением. Это накладывает ограничения на выбор путей между конечными точками.
В каждый момент времени реальный трафик не будет равен зарезервированной полосе пропускания. В соответствие с этим возможны два способа определения величины требуемой пропускной способности для передачи трафика в VPN:
а) статический (Stat). Занимаемая полоса пропускания на ребрах не изменяется со временем;
б) динамический (Dyn). В данном случае происходит периодическое регулирование занимаемой полосы пропускания на ребрах сети.
Соответственно, в рамках данного курсового проекта требуется разработать потоковую модель со следующими параметрами: Asym/T/∞/Stat, а именно: c ассиметричным трафиком конечных точек, древовидной маршрутизацией, бесконечной полосой пропускания сети и статической полосой пропускания на рёбрах.
Задачу проектирования оптимальной структуры VPN можно сформулировать следующим образом.
Дан граф сети 
и
удельная стоимость полосы пропускания: 
= 1
для каждого ребра 
. Для каждой конечной точки VPN 
задано значение входящего/исходящего
трафика 
(множество действительных положительных
чисел).
Требуется
построить на заданном графе дерево VPN 
, для которого справедливо: 
, обеспечивающее наличие уникального
пути для каждой пары конечных точек. При этом суммарная полоса пропускания,
выделяемая на дереве, должна быть минимальной среди всех возможных. Полоса
пропускания ребер не ограничена.
РАЗРАБОТКА АЛГОРИТМА
В статье [2] предлагаются три основных алгоритма для построения потоковой модели VPN с заданными характеристиками:
– метод эллипсоидов;
– прямодвойственный метод;
– полиномиальный метод, основанный на методе поиска в ширину.
Первые
два метода являются базовыми для построения потоковой модели древовидной
маршрутизации с ассиметричным трафиком конечных точек. Расчеты основываются на
совмещении задач целочисленного линейного программирования и расчета дерева
Штейнера для части графа сети. Известно, что проблема расчета дерева Штейнера
является NP–сложной – это
приводит к необходимости использовать аппроксимационные методы расчета. Данные
алгоритмы имеют высокую вычислительную сложность (в теории), однако дают
наиболее приближенное к оптимальному решение. Однако в рамках данной курсовой
работы будет рассмотрен полиномиальный метод, использующийся, в основном, для
расчета потоковой модели с аналогичными характеристиками, но симметричным
трафиком конечных точек. Впоследствии в сравнении с первыми двумя алгоритмами,
это даст возможность для оценки эффективности использования данного алгоритма в
потоковых моделях VPN с заданными характеристиками. В статье [2]
показано, что суммарная занимаемая полоса пропускания дерева, полученная с
помощью данного алгоритма, отличается от полосы пропускания оптимального дерева
на величину, не превышающую значение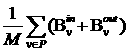 
.
В книге Рослякова А.В. «Виртуальные
частные сети. Основы построения и применения» приводятся основные теоретические
положения, позволяющие определить резервируемую полосу пропускания (
) дерева T.
Будем считать, что суммарная занимаемая полоса пропускания дерева T это сумма занимаемых полос пропускания всех рёбер дерева:
(1)
Определим величину
(2)
как суммарную полосу
пропускания, занимаемую для реализации дерева VPN.
Таким образом, полоса пропускания, резервируемая на ребре в одном направлении,
является минимальной из двух сумм трафиков конечных точек, находящихся по
разные стороны от ребра:
(3)
Предположим, что для дерева T и любой вершины v в нём определена некоторая величина
(4)
обозначающая величину трафика,
которую надо зарезервировать на дереве для связи с любой другой конечной точкой
l. В данной формуле сумма берется по всем
конечным точкам 
, а 
обозначает длину пути между
точками v и l
(выражается в количестве рёбер). В таком случае, для любого дерева, вершинами
которого являются конечные точки VPN, справедливо, что 
удовлетворяет следующим
свойствам:
1.
(5)
2.
(6)
Данные свойства можно проиллюстрировать на примере
ориентированных деревьев. Построим из дерева 
ориентированное дерево 
, при этом определим направление
каждого ребра по следующим правилам:
1.
если 
, то ребро
направлено к вершине i, иначе — к j;
2.
если 
, то ребро
направляется к компоненте, которая содержит определенную конечную точку
(вершину l).
В таком
случае, дерево должно
содержать вершину, которая не имеет входящих ребер, обозначим её как u(T). Для
такой вершины будут справедливы следующие свойства:
1.
(7)
2.
(8)
Из этих
свойств следует, что для оптимального по стоимости дерева 
суммарная занимаемая полоса
пропускания
(9)
Таким образом, задача построения VPN
с оптимальной структурой сводится к нахождению дерева с минимальной суммарной
полосой пропускания. Для этого требуется построить множество деревьев для
каждой вершины в графе G и выбрать среди них дерево с
минимальным значением 
Временная сложность данного алгоритма, изображенного на
рис. 1, равна 
, где m и n — число ребер и
вершин в графе G соответственно. Это объясняется тем, что внешний цикл
алгоритма рассматривает каждую вершину дерева T,
а внутренний цикл в самом худшем случае рассматривает каждое ребро дерева T.
Рис. 1. Алгоритм построения оптимальной потоковой модели VPN с древовидной топологией и асимметричным трафиком конечных точек
РАЗРАБОТКА ПРОГРАММНОЙ РЕАЛИЗАЦИИ АЛГОРИТМА
Алгоритм построения потоковой модели VPN должен быть реализован в программе, разработанной на языке C# с использованием платформы .NET Framework. В качестве графического интерфейса будет использована технология Windows Forms. Это минимизирует затраты на разработку интерфейса программы. Программная реализация разрабатывается в соответствии с принципами объектно–ориентированной парадигмы программирования. Исходный код программы приведен в Приложении Б. Классы, их поля и методы, разработанные в ходе реализации алгоритма, приведены в таблице 1.
Таблица 1
Описание классов программы, используемых для построения потоковой модели VPN
|
Класс |
Поле/метод |
Описание |
|
Node (узел) |
Поля |
|
|
num |
Номер узла |
|
|
isTerminal |
Является ли узел конечной точкой |
|
|
inputTraffic |
Входящий трафик конечной точки |
|
|
outputTraffic |
Исходящий трафик конечной точки |
|
|
links |
Список дочерних рёбер |
|
|
prev |
Ссылка на ребро–родитель |
|
|
Link (звено) |
Поля |
|
|
n1, n2 |
Номера вершин, инцидентных ребру |
|
|
c1, c2 |
Полосы пропускания, выделенные на ребре (от родительской вершины до дочерней и в обратную сторону) |
|
|
weight |
Вес ребра (1 по умолчанию) |
|
|
Tree (дерево) |
Поля |
|
|
root |
Номер корня дерева |
|
|
nodes |
Список узлов дерева |
|
|
sites |
Список конечных точек дерева |
|
|
links |
Список звеньев дерева |
|
|
Методы |
||
|
trim() |
Удаление из дерева листьев, которые не являются конечными точками |
|
|
reserveBandwidth() |
Выделение полосы пропускания на рёбрах |
|
|
getSumBandwidth() |
Вывод величины суммарной занимаемой полосы пропускания дерева |
|
|
Graph (граф) |
Поля |
|
|
n |
Количество узлов графа |
|
|
m |
Количество звеньев графа |
|
|
nodes |
Список узлов графа |
|
|
links |
Список звеньев графа |
|
|
Методы |
||
|
buildOptTree() |
Построение оптимального дерева VPN |
|
|
Traffic |
Поля |
|
|
inputTraffic |
Входящий трафик |
|
|
outputTraffic |
Исходящий трафик |
|
|
GraphDraw (отрисовка графов) |
Поля |
|
|
graph |
Структура – граф |
|
|
tree |
Исходные данные для отрисовки (дерево) |
|
|
net |
Исходные данные для отрисовки (граф) |
|
|
Методы |
||
|
Test |
Создание структуры графа и его изображения |
|
|
FormatVertex |
Определение вида вершины |
|
|
FormatEdge |
Определение вида ребра |
|
Программа должна позволять рассчитывать сети VPN на любых топологиях сетей – топологии должны загружаться из файлов. Структура файла, хранящего топологию рассматриваемой системы:
— количество узлов;
— количество звеньев;
— список всех звеньев.
В программе должна быть реализована возможность выбора топологии типа кольцо, размерностью не более 99 узлов. Конечные точки VPN и их параметры задаются в отдельной таблице, которая хранит в себе следующие данные: номер конечной точки, её входящий и исходящий трафик. Данные из таблицы можно сохранять в соответствующий файл (sites.dat), а также загружать данные из этого файла. Это избавит пользователя от необходимости каждый раз вводить необходимые данные о конечных точках VPN. Полосы пропускания, характеризующие конечные точки, должны иметь значения от 1 до 9999 условных единиц. Соответственно, в программе должна быть предусмотрена проверка данных в таблице на корректность, включая номера конечных точек. Дополнительно, загруженная топология сети из файла должна пройти следующие проверки:
— наличие дубликатов рёбер;
— наличие вершин без инцидентных рёбер;
— наличие рёбер, соединяющих вершины, не находящихся в данном графе.
Главное окно программы показано на рис. 2.
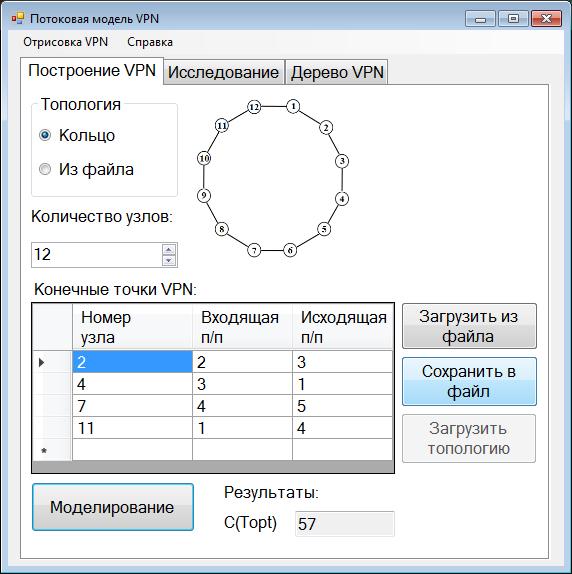
Рис. 2. Интерфейс главного окна программы
Для того чтобы полученное решение было наглядным, следующие параметры построенного дерева VPN должны быть отображены:
— суммарная занимаемая полоса пропускания дерева VPN;
— данные о ребрах (включая зарезервированную на них полосу пропускания) и вершинах дерева VPN;
— визуальное отображение полученного дерева VPN.
Окно вывода табличной информации о построенном дереве VPN показано на рис. 3.
Поскольку задача грамотного отображения графов является достаточно трудоёмкой, то было принято решение использовать стороннее ПО для отображения графа исходной сети и полученного дерева VPN. Из ряда программ была выбрана Graphviz. Данные графов и деревьев из классов передаются в Graphviz с помощью библиотеки QuickGraph. Использование стороннего ПО и заданной библиотеки требует установленного в системе .Net Framework не ниже 4 версии. Окно вывода графов исходной сети и VPN показано на рис. 4.
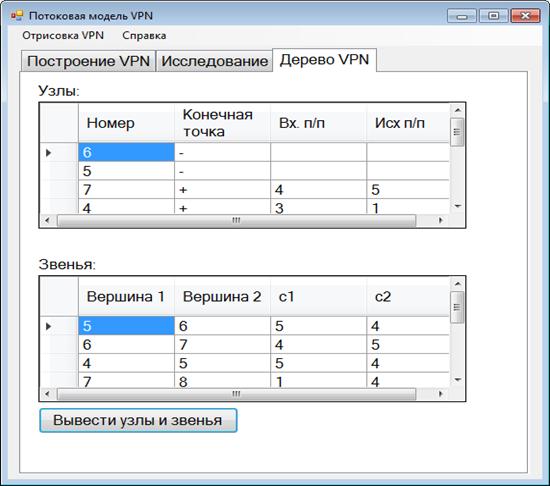
Рис. 3. Интерфейс вывода структур дерева VPN
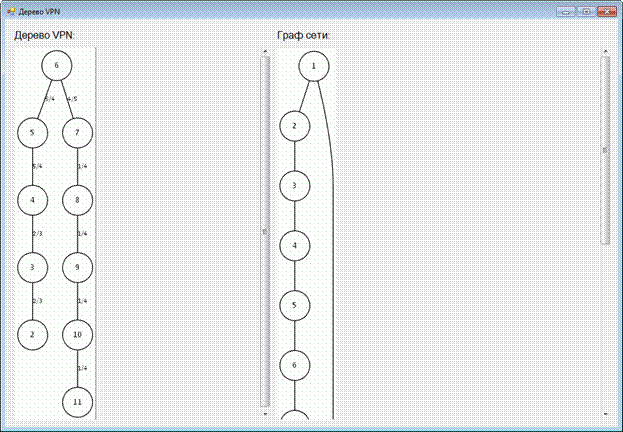
Рис. 4. Окно вывода изображений VPN и сети
Для проведения эксперимента должна быть выделена отдельная таблица, в которой должны быть следующие данные, отображающие ход эксперимента:
— количество конечных точек;
— суммарная занимаемая полоса пропускания дерева;
— время расчета сети с заданными параметрами.
Окно, показывающее информацию о результатах тестирования, отображено на рис. 5.
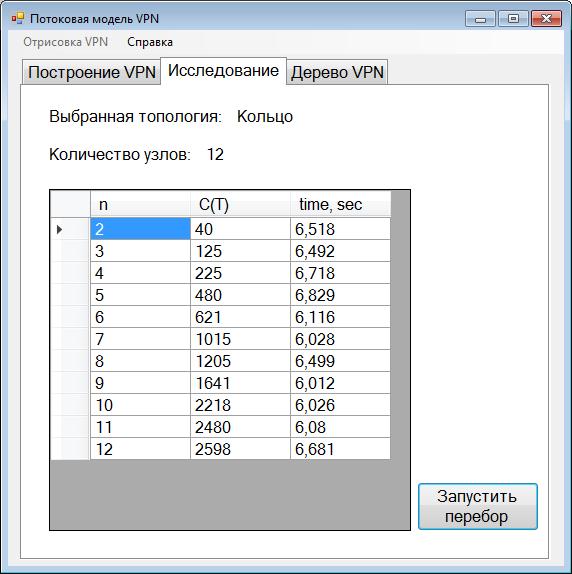
Рис. 5. Окно вывода изображений VPN и сети
РЕЗУЛЬТАТЫ ТЕСТИРОВАНИЯ
Тестирование разработанной программы разделено на 2 части: тестирование построения дерева VPN в рамках алгоритма и тестирование программы на обработку некорректных исходных данных.
Тестирование построения дерева VPN будет проводиться согласно данным, указанным в техническом задании. Топологии сетей: кольцо, NSFNet-16. Тестирование проводится на следующих конфигурациях сетей: кольцо с 3-7 узлами, NSFNet-16 c 5 узлами. Для тестирования топологии типа кольцо берётся любой набор конечных точек n=3. Поскольку в рамках одного расчета дерева VPN перебираются n (по количеству узлов) деревьев, то для одного расчета в рамках тестирования будет рассмотрено 2 произвольно взятых построенных дерева в расчете (всего расчетов 6 – 5 для кольца и 1 для NSFNet–16).
Цифры X/Y, характеризующие рёбра, равны полосе пропускания, резервируемой на ребре от вышестоящей вершины в дереве к нижестоящей и полосе пропускания в обратном направлении.
Тестирование топологии типа кольцо (n=3):
Таблица 2 Данные о конечных точках для топологии типа кольцо (n=3)
|
Номер конечной точки |
Входящий трафик |
Исходящий трафик |
|
1 |
2 |
3 |
|
2 |
3 |
1 |
|
3 |
4 |
5 |
|
|
|
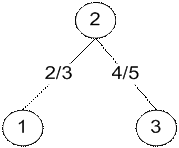
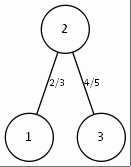
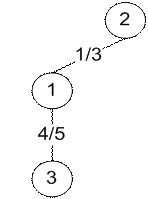
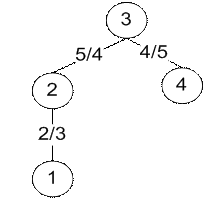
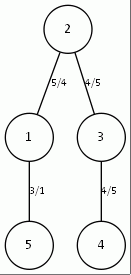
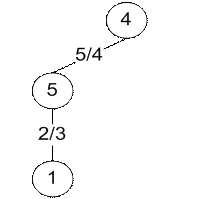
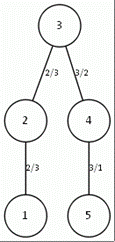
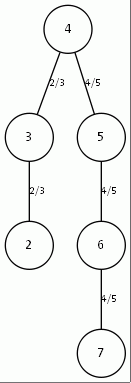
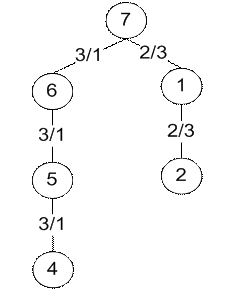
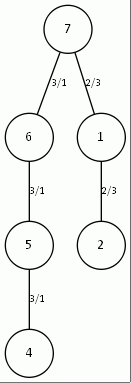
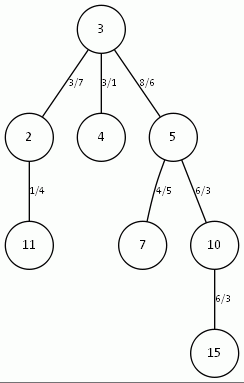
Рис. 6. Дерево, рассчитанное вручную и дерево, рассчитанное программой для топологии типа кольцо (n=3) c корнем в точке 2
|
|
|
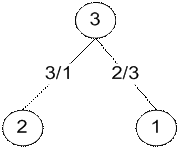
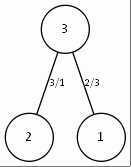
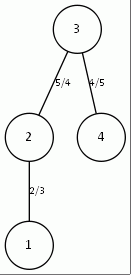
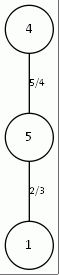
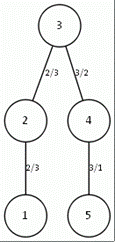
Рис. 7. Дерево, рассчитанное вручную и дерево, рассчитанное программой для топологии типа кольцо (n=3) c корнем в точке 3
Тестирование топологии типа кольцо (n=4):
Таблица 3Данные о конечных точках для топологии типа кольцо (n=4)
|
Номер конечной точки |
Входящий трафик |
Исходящий трафик |
|
1 |
2 |
3 |
|
2 |
3 |
1 |
|
4 |
4 |
5 |
|
|
|
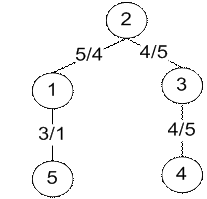
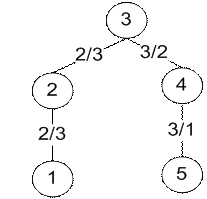
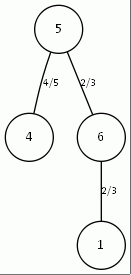
Рис. 8. Дерево, рассчитанное вручную и дерево, рассчитанное программой для топологии типа кольцо (n=4) c корнем в точке 2
|
|
|
Рис. 9. Дерево, рассчитанное вручную и дерево, рассчитанное программой для топологии типа кольцо (n=4) c корнем в точке 3
Тестирование топологии типа кольцо (n=5):
Таблица 4
Данные о конечных точках для топологии типа кольцо (n=5)
|
Номер конечной точки |
Входящий трафик |
Исходящий трафик |
|
1 |
2 |
3 |
|
5 |
3 |
1 |
|
4 |
4 |
5 |
|
|
|
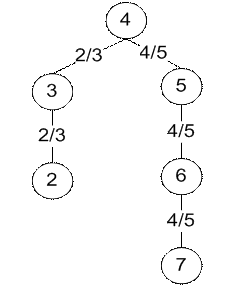
Рис. 10. Дерево, рассчитанное вручную и дерево, рассчитанное программой для топологии типа кольцо (n=5) c корнем в точке 2
|
|
|
Рис. 11. Дерево, рассчитанное вручную и дерево, рассчитанное программой для топологии типа кольцо (n=5) c корнем в точке 4
Тестирование топологии типа кольцо (n=6):
Таблица 5
Данные о конечных точках для топологии типа кольцо (n=6)
|
Номер конечной точки |
Входящий трафик |
Исходящий трафик |
|
1 |
2 |
3 |
|
5 |
3 |
1 |
|
4 |
4 |
5 |
Для точки 3
|
|
|
Рис. 12. Дерево, рассчитанное вручную и дерево, рассчитанное программой для топологии типа кольцо (n=6) c корнем в точке 3
|
|
|
Рис. 13. Дерево, рассчитанное вручную и дерево, рассчитанное программой для топологии типа кольцо (n=6) c корнем в точке 5
Тестирование топологии типа кольцо (n=7):
Таблица 6
Данные о конечных точках для топологии типа кольцо (n=7)
|
Номер конечной точки |
Входящий трафик |
Исходящий трафик |
|
2 |
2 |
3 |
|
4 |
3 |
1 |
|
7 |
4 |
5 |
|
|
|
Рис. 14. Дерево, рассчитанное вручную и дерево, рассчитанное программой для топологии типа кольцо (n=7) c корнем в точке 5
|
|
|
Рис. 15. Дерево, рассчитанное вручную и дерево, рассчитанное программой для топологии типа кольцо (n=7) c корнем в точке 7
Тестирование топологии типа NSFNET-16:
Таблица 6
Данные о конечных точках для топологии типа NSFNet-16
|
Номер конечной точки |
Входящий трафик |
Исходящий трафик |
|
2 |
2 |
3 |
|
4 |
3 |
1 |
|
7 |
4 |
5 |
|
15 |
6 |
3 |
|
11 |
1 |
4 |
|
|
|
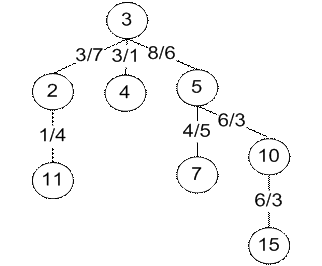
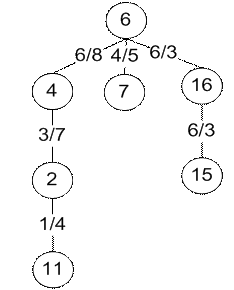
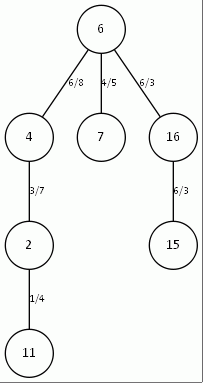
Рис. 16. Дерево, рассчитанное вручную и дерево, рассчитанное программой для топологии типа NSFNet-16 c корнем в точке 3
|
|
|
Рис. 17. Дерево, рассчитанное вручную и дерево, рассчитанное программой для топологии типа NSFNet-16 c корнем в точке 6
Тестирование проверки входных данных на корректность должно проводиться для следующих случаев:
- Номер конечной точки > размер сети
- Повторяются номера конечных точек
- В таблице конечных точек имеется пустое значение
- В таблице конечных точек имеется некорректное значение (>9999)
- Некорректно задана конфигурация графа
Результаты реакции программы приведены на рис. 18 – рис. 19:
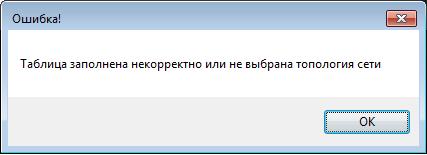
Рис. 18. Результат обработки программы случая некорректного заполнения таблицы конечных точек
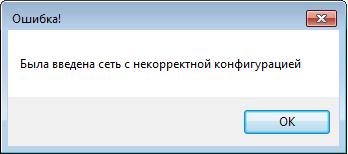
Рис. 19. Результат обработки программы случая неправильно заданной топологии
Программа успешно прошла тестирование как в плане корректности реализации алгоритма, так и в плане обработки вышеописанных возможных ошибок.
Исследование зависимости суммарной полосы пропускания от числа конечных точек VPN
Исследование проводится на трёх топологиях сетей – кольцо , NSFNet-16 и составное кольцо (рис. 20). Впоследствии, полученные данные будут использованы для сравнения эффективности работы выбранного алгоритма с другими алгоритмами.
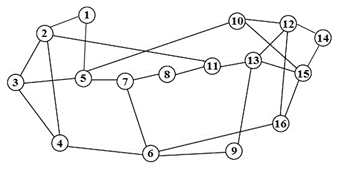
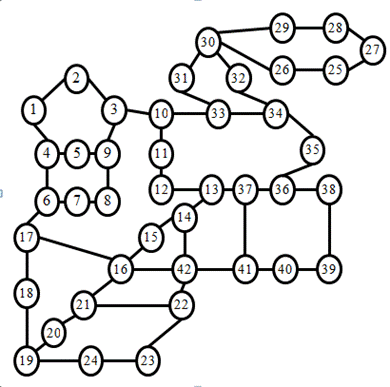
Рис. 20. Топологии сетей NSFNet–16 и составное кольцо
График зависимости суммарной занимаемой полосы пропускания сети от числа конечных точек приведён на рис. 21 и показывает, что при увеличении количества конечных точек в целом рост является линейным, однако для более разветвлённых структур (NSFNet–16) полоса пропускания имеет меньший прирост, чем структуры с малым количеством связей между вершинами – такие как кольцо и составное кольцо. Однако малое количество ветвлений может быть выгодно в плане выбора алгоритма построения дерева VPN: к примеру, полиномиальный алгоритм, возможно, даст более приближенные результаты к решениям апроксимациоными методами построения дерева VPN.
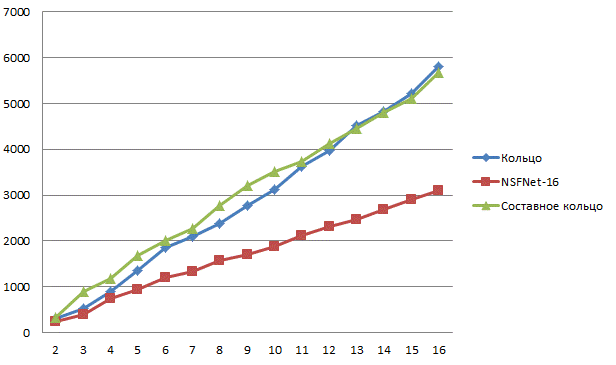
Рис. 21. Зависимость суммарной занимаемой полосы пропускания сети (Кбит/c) от числа конечных точек VPN для трёх топологий сетей
График зависимости времени построения дерева VPN от числа конечных точек (рис. 22) наглядно отображает временную сложность алгоритма – время выполнения зависит только от количества вершин и рёбер. Сопоставимое время выполнения программы для топологий типа кольцо и NSFNet–16 можно объяснить небольшим размером сети (всего 16 узлов).
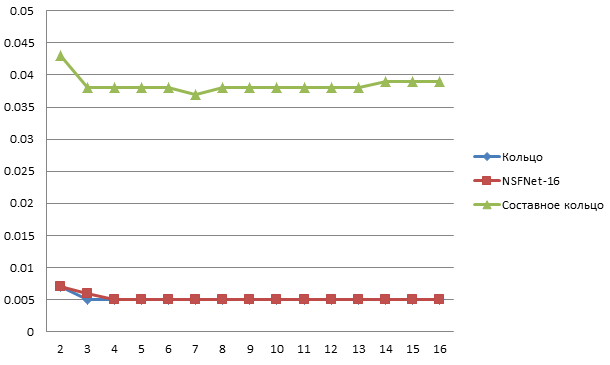
Рис. 22. Зависимость времени выполнения вычислений (с) от числа конечных точек VPN для трёх топологий сетей
Заключение
В результате выполнения данного курсового проекта была разработана потоковая модель VPN c заданными параметрами: ассиметричным трафиком конечных точек, древовидной маршрутизацией, бесконечной полосой пропускания сети и статической полосой пропускания на рёбрах. Полученная модель была реализована в программе, написанной на языке C#. Программа обладает достаточно большим списком функций:
- возможность сохранять список конечных точек в файл и загружать их из файла;
- возможность работать с топологиями, заданными в текстовых файлах;
- получать как табличную информацию о построенном дереве VPN, так и графическую информацию, включая рисунок исходного графа сети;
- возможность получения зависимости суммарной полосы пропускания дерева VPN и времени построения этого дерева в зависимости от числа конечных точек.
Программа успешно прошла тестирование как вычислений в рамках алгоритма построения дерева VPN, так и правильной обработки некорректных исходных данных.
В ходе исследования были получены графики зависимости полосы пропускания дерева VPN и времени выполнения от числа конечных точек и сделаны соответствующие выводы.
Разработанное приложение полностью удовлетворяет требованиям, изложенным в техническом задании, а также является достаточно гибким в плане добавления нового функционала.
1. Kumar A., Rastogi R., Silberschatz A., Yener B. Algorithms for provisioning virtual private networks in the hose model // IEEE/ACM Transactions on Networking. — 2002. — V 10, № 4. — P. 565–578.
2. Росляков А.В. Виртуальные частные сети. Основы построения и применения. — М.:Эко–Трендз, 2006. — 304 с.