СЕТЕВАЯ МОДЕЛЬ РАСЧЕТА УСТАНОВИВШЕГОСЯ РЕЖИМА В ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ СИСТЕМАХ

 

 

Абдулрадх О. А.

 

 

(Москва, Московский энергетический институт (ТУ), Российская федерация)

 

 

 

 

Существует большое количество объектов, которые характеризуются значительной территориальной распределенностью  пунктов контроля и управления. К таким объектам относятся магистральные нефте- и газопроводы, электроэнергетические системы (ЭЭС) и другие крупно масштабные объекты. Сложность управления такими объектами обуславливается, прежде всего большими объемами обрабатываемой информации, оперативного контроля за состоянием объекта по результатам анализа параметров отельных подсистем. Здесь и далее мы сосредоточим внимание на решении одной из важнейших задач управления ЭЭС - на задачи расчета установившегося режима (РУР) эквивалентной электрической сети[1-3].

Обобщенная структура системы управления ЭЭС состоит из национального центра управления (НЦУ) и нескольких локальных центров управления (ЛЦУ) – рис. 1.  Обмен данных и управляющих действии межу НЦУ и ЛЦУ осуществляется через каналы связи со сравнительно малой скоростью. В каждом ЛЦУ хранятся параметры подсети, управляемой им.

В настоящее время характерно использование централизованного подхода к решению такого рода задач, что является «узким» звеном, ведущим к снижению качества управления, прежде всего за счет большой временной реактивности системы, чрезмерной сложности программного обеспечения (ПО) управления данными, вынужденного использования приближенных расчетов (для уменьшения объемов обрабатываемой информации), малой живучести системы. Поэтому разработка новых перспективных подходов для повышения эффективности управления большими системами является в настоящее время весьма важной.

К основным показателям рассматриваемой эффективности относятся быстродействие, надежность получения решения и рациональная организация процессов передачи информации. Перспективный путь в этом направлении заключается: во–первых,  в переходе от последовательных к параллельным вычислениям, во–вторых, в переходе от централизованной к распределенной иерархической организации вычисления.

  В данном докладе описывается разработанный автором метод распределенного параллельного вычисления РУР. Рассматриваемый метод получил название, вынесенное в заголовок данного доклада. Метод основан на следующем обобщении теории Тевенена–Нортона  [4-6].

Суть предлагаемого обобщения заключается в определении напряжении V_th и сопротивления Z_th для всех граничных узлов подсети, а не для одного граничного узла, как в методе Тевенена–Нортона.  

Метод состоит из трёх стадий, которые осуществляются на двух уровнях иерархии.

Нижний уровень выполняется компьютерами, находящими в локальных центрах управления. В этих центрах хранятся параметры своей подсети, управляемой ими.

Верхний уровень  выполняется ведущим компьютером, который находится в главном центре управления. Этот компьютер содержит информацию о топологии сети в целом.

На первой стадии во всех локальных центрах строятся абстрактные схемы замещения  соответствующих электрических подсетей. Абстрактная схема определяет представление каждого граничного узла в виде источника напряжения (V_th) и сопротивления (Z_th) согласно модели Тевенена, или источник тока (I_nor) и сопротивления (Z_nor) согласно модели Нортона.

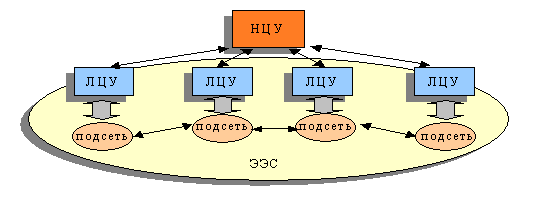
  Рис.1 Обобщенная структура управления ЭЭС  эквивалентов 

 

 Процесс построения эквивалентных схем граничных узлов подсети может происходить параллельно, если есть возможность параллельного вычисления. Данная  стадия выполняется параллельно во всех  локальных центрах, т.е., каждый локальный центр строит модель в виде абстрактной схемы замещения своей подсети. По окончании построения эквивалентных схем подсети, локальный центр посылает значения V_th и Z_th каждого граничного узла ведущему компьютеру, где хранится информация о топологии сети. Понятно, что объем передаваемой информации из локальных центров ведущему относительно невелик.

Вторая стадия алгоритма начинается ведущим компьютером после получения всех значений V_th и Z_th со всех граничных узлов сети. При осуществлении данной стадии строится обобщенная абстрактная модель замещения всей сети. Исходя из этой модели, решается соответствующая система линейных уравнений для того, чтобы найти напряжения в граничных узлах. Число линейных уравнений равно числу граничных узлов. После вычисления значений напряжения в граничных узлах ведущий компьютер посылает полученные значения локальным центрам.

Последняя, третья стадия алгоритма выполняется параллельно всеми вычислителями локальных центров после получения результатов от  ведущего компьютера в виде напряжений на граничных узлах. Здесь вычисляются напряжения, токи и мощности внутренних узлов подсетей. Нахождение искомых значений параметров для всех  внутренних узлов  осуществляется путем решения системы линейных уравнений (СЛУ). Число этих уравнений равно числу внутренних узлов подсети. Рис.2 иллюстрирует предлагаемый распределенный параллельный алгоритм для решения задачи расчета установившегося режима ЭЭС.

    

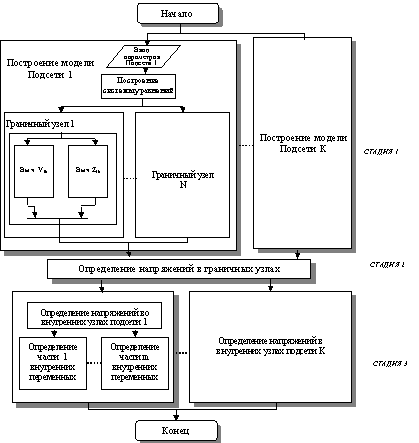
  Рис.2 Схема реализации метода декомпозиционных  эквивалентов 

 

     Рассматриваемый метод представляет собой аналитический подход для решения задачи РУР ЭЭС, когда объем передаваемых данных между процессами относительно не велик. Такое  свойство позволяет применить этот метод в ЭЭС, для которых характерна  значительная территориальная распределенность. Более того,  появляется возможность эффективно использования Internet для реализации предлагаемого метода. Дополнительные свойства метода:

–       равномерное  распределение вычислительной нагрузки на компьютеры, управляющие ЭЭС;   

–       рост коэффициента ускорения параллельных вычислений с уменьшениям связности подсистем ЭЭС.

 

литература

 

1.                 Валях Е. Последовательно-параллельные вычисления / Пер. с англ.- М.: Мир, 1985.- 456 с.

2.                 Родина Н.В. Организация параллельных вычислений в распределённых управляющих системах / Дисс. на соиск. уч. ст. к.т.н.- М.:МЭИ, 1991,-173 с.

3.                 Веников В.А, Строев В.А. Электрические системы электрические сети, Высшая школа, 1998

4.                 http://hyperphysics.phy-astr.gsu.edu/hbase/electric/thevenin.html

5.                 http://www.ee.umd.edu/courses/enee206.F97/206lab08.html

6.                 Татур Т.А., Татур В.Е. Установившиеся и переходные процессы в электрических цепях, Высшая школа, 2001.