PERFORMANCE EVALUTION FOR ENTERPRISE NETWORKS
Abrosimov L.I., Osadchiev A.A.
(Moscow
Power Engineering Institute (TU), Russia)
e-mail: Abros@srv-14.mpei.ac.ru
Abstract.
In this paper formulated the system of the
interconnected definitions of performance for components and computer network
as a whole, functioning in typical modes. Examined the specification of
quantitative parameters of computer networks architecture. Theory allows obtain
quantitative evaluations of computer networks performance in typical modes of
functioning.
1 Introduction
Network managers frequently wants to understand how application traffic is impacting network
performance. Using information from calculations based on proposed theory
enables you to see what applications are using bandwidth, who is using them and
when. Knowing this, when performance issues arise you have a lot of
options: queuing, rescheduling, removing unwanted traffic, reconfiguring
applications that devour bandwidth.
The goal of creation of the theory of computer
networks (CN) performance is development of theoretical basis of calculation
probability-time characteristics of functioning of separate nodes, fragments
and computer networks as a whole which allow to take into account
characteristics of hardware, influence with stacks of reports, which are used
segmentation of messages and work of
users in a dialogue mode.
Basic definitions CN
Computer network (CN) is a technical system containing computers,
connected by communication devices and liaison channels. CN provides remote
performance of information tasks of users.
CN are complex systems,
therefore the efficiency of their functioning cannot be estimated with one
indication, and it is necessary to use a set of characteristics. The basic
characteristics of efficiency of functioning CN are: productivity, reliability,
confidentiality of service and cost.
The productivity of
CN as the system serving users, should be estimated by the number total of
information tasks which are carried out by the all devices included into CN.
Productivity
of the devices, caring out the processing in CN, is determined by technical and
software means of processors, communication devices and channels.
The
basic problem of productivity assessment of implies the CN necessity of
defining and forming key parameters, which influence the CN productivity and
can be quantified, and also working out formulas, allowing to calculate
required parameters of CN productivity.
Consequently,
in order to define of CN productivity it is necessary to create the model with
a set of parameters, reflecting the features of CN functioning from the point
of view of its performance.
In
order to describe CN performance it is necessary to define the processing unit.
During remote service on the user's computer the request for processing
is formed. This request is transferred through channels as the message.
The
processing of the request in each computer is carried out according to the
program of service given by the user (for example, by the kind of processing
included into the list of the menu). According to the type of the program for
processing the request the computer carries out the certain number of calculating
operations.
The
processing of the message in devices of switching and in channels first of all
depends on the volume of the message, measured in bits.
Computer
networks carry out functions of transferring and processing of data and carry
out request transformation to the message and vice versa. The designation of
functionally connected requests and messages we shall call transaction defined by two parameters: the volume of the data and
the number of the computing operations, which are necessary for processing.
That
is why we shall consider transactions of different types as the served units of
work, which determine the CN performance.
For
processing transaction in a channel and in a switching device it is necessary
to allocate the resource of bandwidth for the period required for transferring
the volume of the data, included into the transaction.
For
processing transaction in the computer it is necessary to allocate a
calculating resource for the period of performing the required number of
computing operations.
Thus,
the processing of transaction of any form can be characterized by the invariant
characteristic – the time of the presence of transaction in a serving node.
CN
performance from the point of view of the user should characterize the speed of
processing the transaction of the type, which is considered. From the point of
view of the manager of a network CN performance should reflect the ability of
all the CN resources to process transactions at the stipulated speed of
service.
As a
unit of performance we can use both the intensity estimating the number of
transactions, processed in a unit of time, and the time during which
transaction is processed.
However,
it is necessary to point out, that the presence of various types of
transactions in CN may result in the ambiguity of these ratings. Therefore: the
structure, the communications and the characteristics of the kind and name of
subscribers, and the routes of transactions should be defined.
The
presence of different requirements and application of decomposition of various
degree at the description of processing transactions in CN results in the
necessity of using several ratings of CN performance forming system of concepts of CN performance to
which first of all:
- CN
performance of elements,
- CN
performance of nodes,
-
Complex CN performance,
-
Working CN performance,
-
Peak CN performance,
-
Limiting of CN performance for considered type of transactions at peak loading.
2 The specification of parameters
The
essence of the offered approach is, that the stream of transactions circulating
in CN, may is considered as consisting of several type of transactions, and in
each of the type (closed or unclosed)
transaction goes along a route named a
contour, passing through the fixed sequence of serving CN nodes.
For
the description of the model of functioning of CN we introduce the
specification of parameters of architecture (AR) which is determined by three
groups: AR = < ST, TR, DT >, where ST is a group of parameters of
topological structure; TR a group of parameters of structure of transactions;
DT a group of parameters of dynamics of transactions.
ST =
< R, V, E, S >, where R a set of regions of CN ; V - set of V nodes (r,
e) of the region; Е - set of elements Е (r, v, e), S - structure of functional
communications CN.
On
fig. 1 there is an example of nodes and regions of CN fragment where the region
1 (r=1) contains three nodes V (1,1), V (1,2), V (1,3). Each node models the
device providing the delay of transactions for the period of processing, and is
considered as a single-channel system of mass service, for example, 
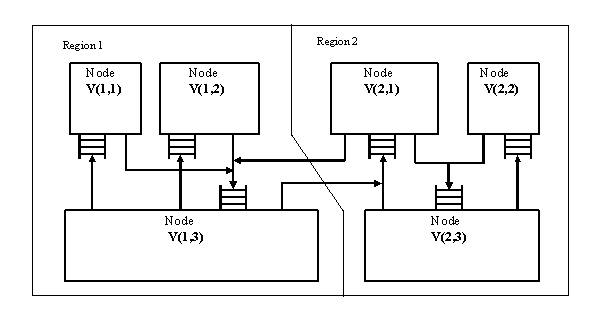
Fig
1. An example of performance of nodes and regions of fragment CN
Elements
Е(r, v, e) of serving nodes
display the units of processing, which temporarily focus resources of node V(r,
v) for processing transaction of examined type to create, for example, a
process or to start a subroutine. To illustration this fig. 2 shows, that
V(1,1) node contains two elements: E (1,1,1) and E (1,1,2).
TR =
< Q, Ф, P, M, C, A >, where Q – are the functions, determining contours q. Ф -
the functions determining phases φ of contours q. Р -
functions of probabilities of transition of transactions of a contour q from an
element to an element. M - the functions specifying factors m, which means the
change of transactions number of a phase φ of a contour q. C - the
functions specifying the capacity of closed contour ZQ(q). A - functions
specifying the priority of processing in the node of transactions of a given
phase φ of contours q.
Q(q) is conditionally allocated way of movement
through nodes and elements of a network of transactions which have identical
parameters at processing refers to as as contour Q. An example of performance
of three closed contours for fragment CN
is represented on fig. 2. As shown, transactions of closed contour Q (1)
circulate on a route: E (1,1,1), E (1,1,2), E (1,3,1), E (1,2,1), E (1,2,2) and
E (1,3,2).
The
phase of a contour is a part of a contour in which each node serves transaction
only one time. As shown in fig. 2 contour Q (1) has two phases: φ 1 which includes elements E (1,1,1), E (1,1,2), E (1,3,1), E (1,2,1), E
(1,2,2), and φ 2 which includes element Е (1,3,2).
Probabilities
p (r, i, v, j, e, k, q, φ) of transactions of a contour q phases: φ from element E (r, v, e) to element E (i, j, k). They define the
possible directions of transition of transactions from an output of the serving
element on an input of the subsequent element and they are displayed by focused
arches.
The
factor m (r, i, v, j, e, k, q, φ) which are defines the change of the number of phase φ
transactions of a contour q shows how many time higher (m > 1) or lower (m
< 1) the number of transactions has become when transactions goes from an
input of element E (r, v, e) up to an input of element E (i, j, k).
Capacity
C (q) of the closed contour ZQ (q) defines the number of the transactions
circulating in a closed contour given in base value.
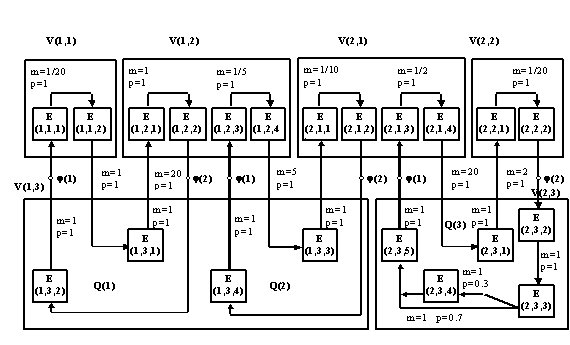
Fig 2. An example of performance of three
closed contours for CN fragment
DT = < FX, FY, N, T >, where FX are
functions of distribution of probabilities of a holding time of transactions of
the given phase φ contours q by each element Е (r, v, e). FY are functions
of distribution of probabilities of time of receipt of transactions of the
given phase φ a contour q on an input of nodes V(r, v). N - set of values of average number of transactions of the given phase
φ contours q which are taking place in turn and in the node. T is a set
of values of an average holding time of transaction by each element the node Е (r,
v, e).
3
The parameters determining CN performance
Taking into account the stated specification of
parameters and the deduced ratios it is possible to define the system of
concepts of CN performance as follows.
CN Performance of elements is estimated
by:
- a set of intervals of time 
( r, v, e, q, φ), which each element E (r, v, e) of each
serving node spends on the processing transactions for each phase φ of contours q,
- a set of intensities m (r, v, e, q, φ)
of processing each serving node of transactions
by each element E (r, v, e) for each phase for contours q, where m (r, v, e, q,
φ) = 1/
( r, v, e, q, φ)
,
- a set intensities λ (r, v, e, q, φ) of transactions coming to the input of element E (r, v, e) of the
serving node for each phase φ of contours q, where λ (r, v, e, q, φ)
= 1/
( r, v, e, q, φ)
.
Nominal parameters of elements E (r, v, e)
depend on the parameters of hardware and software of each CN element and on the
types of process at transactions. Functional dependences of nominal parameters
of elements E (r, v, e) on the parameters of CN elements VS and on the types of
transactions are set with the help of
experimental methods.
CN
Performance of nodes is estimated by:
- a set of intervals of time
( r, v, q, φ), which each serving node V (r, v) spends on processing transactions
for each phase φ of contours q,
- a set intensity m (r, v, q, φ) of processing transactions by each serving node for each phase φ of contours q, where M (r, v, q, φ) = 1/
( r, v, q, φ).
System parameters of nodes can be calculated
with the help of the should nominal parameters, but be checked experimentally.
Complex
CN performance is estimated by:
- a set of intervals of time tк(q), the corresponding set of
serving nodes V(r, v) spends on processing each considered type of transactions
for each phase φ of contours q where
- a set Intensity λк(q) = λ(r0,v0,q) of the processed traffic of each
considered type of transactions of contours q in the appropriate basic serving
node V(r0,v0) the ratio ρ(r,v,q)
= ρ (r,v) is true for the loading factors of all serving nodes.
Complex performance of transactions can be
calculated with the help of system parameters of nodes and be checked
experimentally.
Working
CN performance is estimated by:
- the set of the intervals of time tp(q), the appropriate set of
serving nodes V(r, v) which spends at processing each considered type of the
transactions of q contours at a known parity of the types of transactions of
the contours q
Q, which form the working traffic, in that case appropriate to model
M/M/1 for CN nodes:
the set of intensity λр(q) = λ(r0,v0,q) of the processed traffic of each
considered type of transactions of contours q in appropriate base serving node
V(r0,v0) at a known parity of types of transactions of
contours g
Q, which form the working traffic of loading.
Peak
CN performance is estimated by:
-the set of intervals of time t * (q), which spends at processing each
considered(examined) type of transactions of contours q in appropriate base
serving node V(r0,v0) at a known parity of types of transactions
of contours g*
Q, that make the peak traffic of loading. In the case
for CN
nodes appropriate to model M/M/1.
- the set Intensity λ*(q) = λ(r0,v0,q)
of the processed traffic of each considered type of transactions of contours q
in appropriate base of serving node V(r0,v0) at a known
parity of the types of transactions of the contours g*
Q, that make the peak traffic of loading.
Limiting
CN performance for considered type of transactions at peak
loading is estimated by:
- the set of intervals of time tп(q),
which the appropriate set of serving nodes spends at processing each considered
type of transactions of contours q at a known parity of types of transactions
of contours gп
Q, that make the peak traffic of loading, and a maximum load in one of
serving CN nodes. In that case
for CN nodes appropriate to model M/M/1.
- the set Intensity λп(q) = λ(r0,v0,q) of the processed traffic of each
considered type of transaction of contours q in appropriate base serving node
V(r0,v0) at a known parity of types of transactions of
contours gп
Q, that make the peak traffic of loading, and a maximum load in one of
serving CN nodes.
4
Calculation of the CN performance
The method of contours developed by the author
[1,2,7] is used as a basis for calculation of parameters of CN performance. In
view of the stated specification of parameters of CN architecture definition of
CN performance will demand performance of the following stages.
The description of topological structure
researched by CN in parameters of group ST = < R, V, E, S >.
The description of structure of the traffic of
transactions by parameters of group TR = < Q, Ф, P, M, C, A >.
The description of dynamic parameters of each
element Е (r, v, e) by parameters of group DT = < FX, FY, N, T >.
Calculation of dynamic parameters of nodes V(r,
v).
Each node V(r, v) is considered as a system of
mass service, in which transaction of the appropriate contour q are delayed for
the period of service in the node and for the period of expectation in turn.
The holding time in the node is defined by the convolution of function FX (r,
v, e) of distributions of probabilities of a holding time by each element E(r,
v, e) of transactions of the appropriate phase φ a
contour q., Any way branching algorithm of interaction of elements is
represented in the series-parallel form in order to the use of Laplas
transformations which are carried out for calculation Probability -time
characteristics (PTC) of CN nodes, each branch ц(b), (where b =
) which begins at entrance element Е(е0) and ends at terminal element Е(ек) and has for each branch probability ά(b,
r,v,e,q,φ). Then the first
and the second
. The moments of a holding
time in node V(v) transactions of a contour q may be calculated on parities
[2]:
5
Working out and calculating linear equations
Assuming the absence of losses of messages, at
a stationary mode processing them in CN the calculated characteristics of nodes
V(r, v) allow to work out linear equations for each node. These equations link
intensity λ(r,i,v,j,e,k,q,φ) of the stream of transactions for each phase φ of contours q coming from the
outputs of nodes V(r, v) to the
input of nodeV (i, j) with Intensities λ(0,r,0,v,e,q,φ) and λ(i,r,j,v,e,k,q,φ) of the stream of transactions for each phase φ of contours q, coming to the input of node V(r, v) from the outputs of
nodes V (i, j) and from the external source V (0, r).
For closed contours ZQ(q) the intensity of the
input stream of transactions is not known and consequently the solution of
system of the linear equations allows to determine only the weighed factors a(i,r,j,v,e,k,q,φ) of basic intensity λ(r0,v0,q) of the stream
of the transactions, calculated in relation to the base node V(r0,v0). Thus, the calculated factors a(i,r,j,v,e,k,q,φ) allow to determine the value of any intensity λ(i,r,j,v,e,k,q,φ) of the stream of transactions, using a the
ratio:
λ(i,r,j,v,e,k,q,φ) = a(i,r,j,v,e,k,q,φ) λ(r0,v0,q) (4)
6
Working out the solution of the nonlinear equations
In order to calculate the base intensity λ(r0,v0,q) of the stream of transactions for each
closed contour q you should work out the additional nonlinear equation
presenting (for each contour q at the stationary mode of functioning) the
condition of equality of the sum of normalized transactions in the nodes of the
contour to the value of capacity C(r0,v0,q) of this
contour.
In the ratio (5) function N(r,v,q,φ) expresses the dependence of the number of the transactions which are
served in node V (r, v) on the intensity
λ(i,r,j,v,e,k,q,φ) of the coming stream of transactions and on
the first and the second moments of serving of
transactions of contour q in node V(r,v). The kind of functions N(r,v,q,φ) depends on the chosen
mathematical model serving node. As a result of solving the system of nonlinear
equations the values of basic Intensities λ(r0,v0,q)
calculated for each contour q.
Examples of working out and the joint solving of the system of
nonlinear equations can be found in [1 - 8].
7
Calculation of parameters of CN performance
After calculating the of dynamic parameters and of
nodes V(r,v) and Intensities λ(i,r,j,v,e,k,q,φ) of
the streams of transactions in all the serving CN nodes all parameters of CN
performance or only required ones are calculated according to the introduced
system of concepts of CN performance.
You can see the examples of calculations in [1
- 8].
8
Conclusion
The article represents methodological
foundation of the theory of computer networks performance of which is based on
the specification of parameters for the description of functioning of CN and on
the mathematical ratios for calculation of probability-time characteristics of
CN. As it was shown, the suggested approach gives engineers the opportunity for
reasonable choice of design options and, in the author’s opinion, the suggested
concept can be developed and for other assesments of quality of functioning CN
(reliability, survivability, etc.).
The carried out research has allowed to reveal,
formulate and determine the operations
which are necessary to perform during decomposition for describing CN and which
involve: allocation of nodes (V) and regions (R), defining of types of nodes in
regions, allocation of functional levels in the nodes appropriate to structures
of used reports, defining subscribers - sources and subscribers - addressees of
the data, revealing and recording the contours of transferring of transactions
between CN nodes as a sequence of the nodes participating in processing of
transactions, allocation of the phases of the contours taking into account the
features of used structures of reports, drawing up of the list of necessary
characteristics for modelling CN.
Now we
have the first results of the use of the formulated decomposition procedures of
CN description for the reports with consecutive transfer of transactions and
parallel transfer of transactions, reports SNA and TCP, reports of processing
transactions at an applied level.
In order to describe the functions of
consecutive transfer of the data packages the standard nodes of architecture
ISO are considered. Different levels: applied, sessional, transport and channel
in various combinations - use the mechanisms of transfer and without
aknowledgement of receipt, with a window for transfer.
References
Методы
автоматизированного проектирования систем телеобработки данных// Учеб. пособие
для вузов/ В.А. Мясников, Ю.Н. Мельников, Л.И. Абросимов. - М.: Энергоатомиздат,-
1992. - 288 с.: ил.
Абросимов Л. И.
Методология анализа вероятностно-временных характеристик вычислительных сетей
на основе аналитического моделирования. Диссертация на соискание ученой степени
доктора технических наук . Москва.: МЭИ, 1996.
Abrosimov L.I. Modellierung von
Datenuebertragungprotokellen mittels Tensoranalyse zur Bestimmung der
Uebertragungscharakteristiken von Rechnernetzwerken. 40 Internationales
Wissenschaftliches Kolloquium 18.-21.09.1995. Technische Universitaet Ilmenau Thueringen.
Band 1, s.235-240.
Абросимов Л.И.
Концепция разработки интеллектуальной платформы администрирования гетерогенных
вычислительных сетей на базе моделей с тензорными преобразованиями,
Международная Академия Информатизации, 1997, Московский Энергетический
Институт, Том 1, с.60-67.
Abrosimov L.I. Conception of creation of intelligent
integrated management platform for heterogeneous computer networks on the basis
of tensortransform modeling. International Conference DISTRIBUTED COMPUTER
COMMUNICATION NETWORKS. Theory and Applications 4 - 8.11.1997 Tel-Aviv
(Israel). Institute for Information Transmission Problems RAS, Tel-Aviv
Universiti, M:. 1997 s.3 - 11.
Abrosimow L.I., D. Reschke, A.W. Emekeew Methodik und
Ergebnisse der Zeitparametermessung bei der Paketenlieferung in realen LAN ATM
und Ethernet. 43. Internationales Wissenschaftliches Kolloquium 21.-24.09.1998
. Technische Universitaet Ilmenau Thueringen. Band 1, s.235-240.
Абросимов Л.И.
Анализ и проектирование вычислительных сетей: Учебное пособие - М.:, Изд-во
МЭИ. 2000. - 52 с.
Lehr- und Uebungsbuch Telematik /Hrsg. Gerhard Kruger ; Dietrich Reschke. Autoren Leonid I. Abrosimov, Jorg Deutschmann, Werner Horn, Holger Reif, Dietrich Reschke, Jochen Schiller, Jochen Seitz. Muenchen; Wien:Fachbucherverl. Leipzig im Carl-Hanser-Verl., 2000.S 85-98 (412 s)