BC/NW 2017 № 1 (30):10.1
СИСТЕМА АВТОМАТИЗИРОВАННОГО РАСЧЕТА ХАРАКТЕРИСТИК ТИПОВЫХ СХЕМ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
Дорошенко А.Н.
Введение
Излагаемая здесь система (Система Автоматизированного Расчёта Характеристик СМО - САРХ) предназначена для компьютерного выполнения расчётов характеристик типовых схем СМО с целью ускоренной проверки выполнения контрольных работ, домашних заданий студентов, изучающих разделы построения и исследования аналитических моделей схем систем массового обслуживания, а также для самопроверки студентами своих знаний и умения решать соответствующие задачи.
В состав типвых схем СМО в САРХ включены, во-первых, четыре схемы, для которых обычно в учебно-методической литературе по аналитическому моделированию СМО приводятся формулы расчета и студент должен по текстовому описанию задания аргументированно определить принадлежность своей схемы к определённому типу схем СМО, а дальше, подставляя в известные формулы типовой схемы исходные данные, вычислить характеристики моделируемой системы. К таким схемам относятся одноканальные и многоканальные СМО с отказами (без очереди) и одноканальные и многоканальные СМО с неограниченной очередью.
Во-вторых, в САРХ включена схема, называемая в теории массового обслуживания как «Схема гибели и размножения» (СГиР) (название это появилось от применения её для исследования жизнедеятельности популяций в биологии). Для наших целей применение СГиР по существу позволяет проводить расчеты характеристик определённой группы схем – схем моделей информационных, управляющих, материальных потоков в различного рода системах массового обслуживания – характеризующихся наличием ограниченной очереди заявок, а именно, одноканальных и многоканальных СМО с ограниченной очередью, что требует от студентов некоторых размышлений, правильной трактовки схемы СГиР, построения графа состояний моделируемой схемы и сопоставления его с графом состояний соответствующей СГиР (то есть с графом СГиР, совпадающим по структуре и по количеству вершин графа состояний схемы СМО индивидуальногого задания).
Адаптация «Схемы гибели и размножения» к конкретной типовой СМО состоит в правильном представлении графа состояний моделируемой системы (а самое главное – в правильном назначении весов рёбер графа – стрелок переходов моделируемой системы из одного состояния в другое) и в сопоставлении этого графа с вариантом графа СГиР, то есть адаптация состоит в том, что студенту требуется выполнить следующиую последовательность действий:
· определить количество состояний (вершин графа) моделируемой системы,
· установить связи между состояниями (вычерчивание направленных рёбер, соединяющих вершины графа),
· задать веса рёбер графа - интенсивности переходов моделируемой системы из одного состояния в другое (запись весов графов).
Примечание. Для правильного выполнения последнего пункта следует, во-первых, понимать что такое событие в СМО (формально это переход моделируемой системы из одного состояния в другое, а фактически – появление заявки в системе, или завершение обслуживания заявки, или удаление заявки из системы). Во-вторых, понимать, что одновременно выполняющиеся действия (обслуживание заявок в многоканальных устройствах) – независимы и поэтому вероятности их завершения суммируются, следоватенльно, суммируются интенсивности перехода из одного состояния в другое.
Далее по графу состояний СГиР записать для каждого из состояний S0, S1, S2,…, Sn записать соответствующие им формулы вычисления вероятностей P0, P1, …, Pn, этих состояний (детализация этих процедур будет раскрыта на конкретном примере в разделе 5).
Ниже рассмотрены варианты рассчётов схем СМО в САРХ. Система реализована в среде DELPHI.
Примечание. Предплагается, что все случайные процессы в рассматриваемых в САРХ аналитических моделях, то есть все потоки случайных событий, связанных с появлением заявок на входе системы и с завершением обслуживания в каналах СМО, обладают тремя свойствами простейшего потока: свойством стационарности, свойством без последействия и свойством ординарности.
Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени.
Важнейшей
характеристикой потока событий является его интенсивность, обозначаемая обычно
греческими буквами ![]() ,µ.
,µ.
Интенсивностью называется
среднее число событий, появляющихся за единицу времени. В частности, интенсивность
стационарного потока – величина постоянная, не зависящая от времени ![]() = const.
= const.
Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени t1 и t2 число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. По сути это означает, что события, образующие поток, появляются в те или другие моменты времени независимо друг от друга, вызванные каждое своими собственными причинами.
Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами — по нескольку сразу. Если поток событий ординарен, то предполагается, что вероятностью попадания на малый участок времени dt двух или более событий можно пренебречь, так как она несоизмеримо меньше, чем вероятность попадания одного события.
Поток событий называется простейшим (или стационарным пуассоновским), если он обладает всеми тремя свойствами: свойством стационарности, свойством без последействия и свойством ординарности.
В первой компьютерной форме (Рисунок 1) содержится перечень из пяти вариантов выбора схем моделируемых СМО:
1. Одноканальная система массового обслуживания без потерь заявок;
2. Одноканальная система массового обслуживания с отказами
3. Многоканальная система массового обслуживания
4. Многоканальная система массового обслуживания
5. Схема гибели и размножения
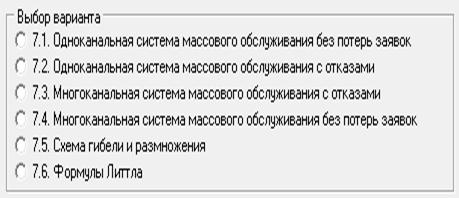
Рисунок 1. Варианты режимов работы системы
1 Расчет характеристик одноканальной СМО с обслуживанием
Исходными данными для такой схемы являются интенсивность входного потока заявок λ и интенсивность обслуживания заявок в канале µ (или средние интервалы времени, соответственно, Твхода =1/ λ, Тобсл= µ).
В одноканальной СМО с обслуживанием предполагается наличие неограниченной очереди. При этом естественным является требование обеспечения работы системы в ненасыщенном режиме, то есть при неограниченном времени наблюдения за процессом функционированиния такой СМО длина очереди не должна расти неограниченно. Практически это означает, что интенсивность входного потока заявок должна быть меньше интенсивности обслуживания завок в канале, то есть должно выполняться отношение λ/µ<1 для одноканальной СМО. Это отношение называется коэффициентом загрузки канала или вероятностью занятости канала и, естественно, может принимать значение из интервала (0,1).
При нарушении этого условия расчёт невозможен и система защищена от некорректного задания исходных данных, выдавая сообщение: «Коэффициент загрузки системы λ/µ > 1, сверхнасыщенный режим работы системы».
При корректно заданных данных получаем результаты расчета (смотреть компьютерную форму на рисунке 2), сопровождаемые схемой процесса, графом состояний системы, который имеет неограниченное количество состояний, соответствующее неограниченной очереди. Вероятность любого k-того состояния может быть вычислена при задании соответствующего значения k.
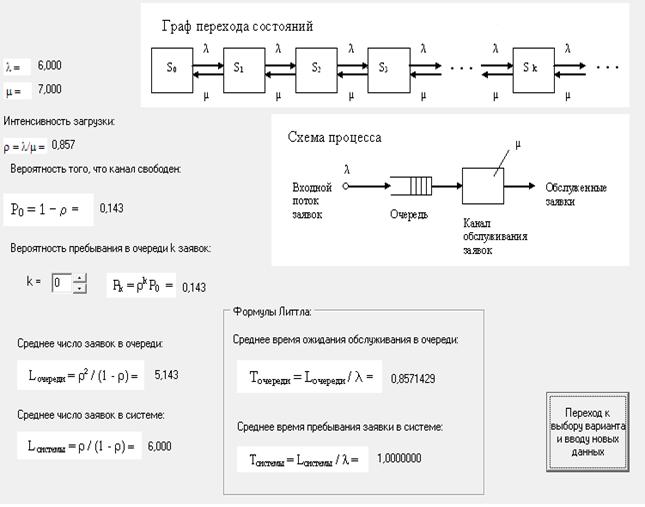
Рисунок 2. Результаты расчёта характеристик одноканальной системы с неограниченной очередью (с обслуживанием без потерь заявок)
Для данной СМО вычисляются также автоматически средняя длина очереди и среднее число заявок, находящихся в СМО, а также вычисляемые по формулам Литтла среднее время ожидания в очереди и в среднее время нахождения заявок в системе (то есть среднее время отклика системы на запрос, поступающий в систему.
2 Расчет характеристик одноканальной СМО с отказами
Исходными данными для этой схемы (компьютерная форма приведена на рисунке 3) также являются значения интенсивностей входного потока заявок и обслуживания их в канале, однако не требуется выполнение какого-либо условия, так как при поступлении завки в СМО в тот момент времени, когда канал занят, эта заявка исчезает (в системе имитационного моделирования она уничтожается).
Работа СМО представлена графом, отображающим два состояния системы: S0 – система свободна от заявок и S1 – занята обслуживанием одной заявки. Для этой СМО вычисляется следующий набор характеристик: вероятности состояний системы P0, P1, вероятность отказа системы в обслуживании заявок Ротказа = Р1, вероятность обслуживания или относительная пропускная способность системы Q=1 - Ротказа = Р0, абсолютная пропускная способность, определяемая как количество заявок, которое может быть обслужено системой за единицу времени (за секунду, минуту, …).

Рисунок 3. Результаты расчёта характеристик одноканальной системы с отказами (с обслуживанием заявок без образования очереди)
3 Расчет характеристик многоканальной СМО с отказами
Для рассчета характеристик этой схемы (компьютерная форма результатов расчета приведена на рисунке 4), кроме интенсивностей входного потока и обслуживания заявок в канале, следует задать количество каналов n, параллельно обрабатывающих заявки, поступающие в систему.

Рисунок 4. Результаты расчёта характеристик многоканальной системы с отказами
К исходным данным этой системы, как и для одноканальной СМО без очереди, не требуется выполнение какого –либо условия, так как при поступлении завки в СМО в тот момент, когда все n каналов заняты, эта заявка удаляется из системы и она не оказывает никакого влияния на состояния системы.
Работа СМО представлена графом, отображающим n+1 состояний: система свободна или занята обслуживанием от одной до n заявок. Для этой СМО вычисляются: вероятности состояний P0, P1,…,Рn, вероятность отказа системы Ротказа = Рn, относительная пропускная способность или вероятность обслуживания Q=1 - Рn, абсолютная пропускная способность, то есть количество заявок, обслуживаемых СМО за единицу времени, среднее число занятых каналов, среднее число заявок, находящихся в системе и среднее время пребывания заявки в системе (среднее время обслуживания или среднее время отклика системы).
4 Расчет характеристик многоканальной СМО с обслуживанием
Исходными данными для рассчета этой схемы (компьютерная форма приведена на рисунке 5) являются, как и в предыдущем варианте, три параметра: интенсивности входного потока заявок и обслуживания их в канале и количество каналов n многоканальной СМО.
В многоканальной системе с обслуживанием предполагается наличие неограниченной очереди. При этом естественным является требование обеспечения работы системы в ненасыщенном режиме, то есть при неограниченном времени наблюдения за процессом функционированиния такой СМО длина очереди не должна расти неограниченно. Практически это означает, что отношение интенсивности входного потока заявок к общей интенсивности обслуживания в n каналах должна быть меньше единицы и это отношение будем называть коэффициентом загрузки многоканального устройства. При нарушении этого условия расчёт невозможен и система защищена от некорректного задания исходных данных, как и в случае рассмотренного выше варианта 1, выдавая сообщение: «Коэффициент загрузки системы (λ/(n*µ) > 1, сверхнасыщенный режим работы системы».
Результаты работы АСРХ при корректном задании исходных данных для многоканальной СМО с обслуживанием представлены на рисунке 5.

Рисунок 5. Результаты расчёта характеристик многоканальной системы с неограниченной очередью (с обслуживанием без потерь заявок)
Работа СМО представлена графом, отображающим неограниченное число состояний (S0, S1, S2,…, Sn ): система свободна - S0 или занята обслуживанием от одной до n заявок без очереди - S1, S2,…, Sn, а затем состояния, при которых возникает очередь – Sn+1, Sn+2,…, Sn+R,… . Для этой СМО могут быть вычислены вероятности состояний P0, P1,…,Рn, Рn+1,…, Рn+R,… . Вероятность любого (n+R)-того состояния может быть вычислена при задании соответствующих значений k и R. Для данной СМО вычисляются также автоматически среднее число занятых каналов, средняя длина очереди и среднее число заявок, находящихся в СМО, а также вычисляемые по формулам Литтла среднее время ожидания в очереди и в среднее время нахождения заявки в системе (то есть среднее время отклика системы на запрос, поступающий в систему).
5 Расчет характеристик одноканальной и многоканальной СМО с ограниченной очередью
Для расчета характеристик любой СМО с ограниченной очередью в системе АСРХ применяется режим работы «Схема гибели и размножения». Прежде всего требуется построить для заданной схемы СМО граф состояний, по структуре совпадающий с графом СГиР, но имеющий особенноси, определяемые структурой заданной СМО. В качестве исходных данных для расчета характеристик СМО в АСРХ задаётся, во-первых, n – общее число состояний СМО, и во-вторых , две группы наборов значений интенсивностей как весов рёбер графа, связывающих n состояний в цепочку. При этом наборы интенсивностей определяются из графа состояний, построенного для заданной конкретной схемы СМО.
В качестве примера ниже на рисунках 6.А и 6.Б приводятся результаты расчёта характеристик трёхканальной СМО с очередью, ограниченной двумя местами. Тогда общее число состояний системы будет равно n =6.
Пусть интенсивность входного потока заявок задаётся равной 5 заявок в секунду, интенсивность обслуживания в одном канале равна 1,5 заявки в секунду. Следовательно, интенсивности верхнего ряда, задающие частоту перехода по графу состояний слева направо, одинаковы и равны 5, так как определяются появлением на входе системы заявок при условии незавершенного процесса обслуживания заявок, поступивших в систему ранее, а интенсивности перехода нижнего ряда, задающие частоту перехода по графу состояний справа налево (частоту завершения одного из независимых процессов обслуживания в каналах трёхканальной СМО), определяются количеством процессов обслуживания (от 1 до 3), выполняемых трёхканальным устройством в соответствующем состоянии СМО: 1,5; 3; 4,5; 4,5; 4,5.
Таким образом, для заданной в примере системы обслуживания могут быть рассчитаны следующие характеристики: вероятности всех состояний системы и, как следствие, вероятность отказа, вероятность обслуживания или относительную пропускную способность, абсолютную пропускную способность системы, среднее число занятых каналов, среднюю длину очереди и среднее время ожидания заявок в очереди, среднее время отклика системы и другие характеристики системы.
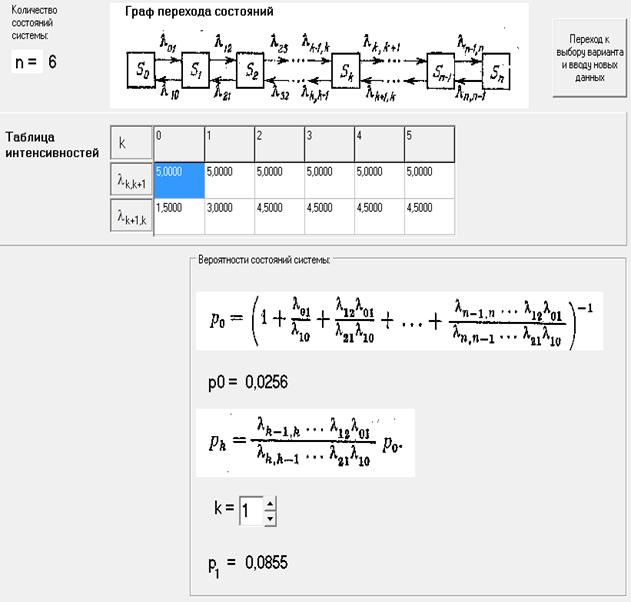
Рисунок 6.А. Результаты расчёта характеристик трёхканальной системы с очередью, ограниченной двумя местами (СМО с потерями заявок, пытающихся войти в систему при полной занятости мест в очереди): Р0 – вероятность состояния простоя системы, свободной от заявок и Р1 – вероятность состояния трёхканальной системы, занятой обслуживанием одной заявки в одном из каналов
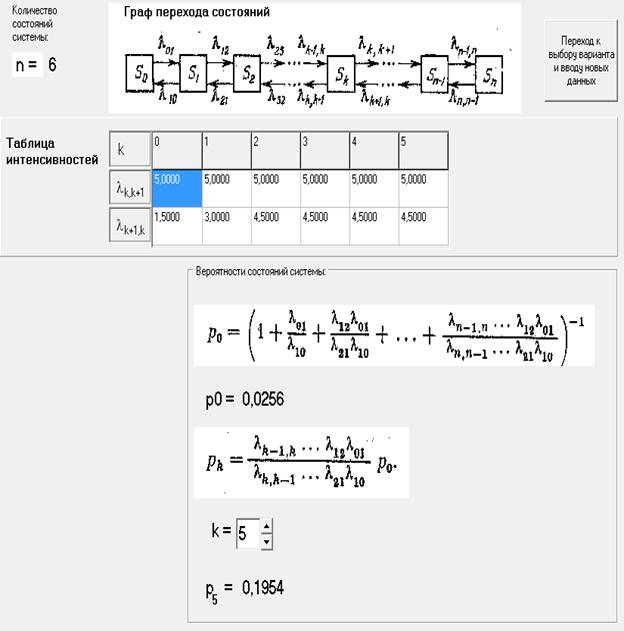
Рисунок 6.Б. Результаты расчёта характеристик трёхканальной системы с очередью, ограниченной тремя местами (СМО с потерями заявок, пытающихся войти в систему при полной занятости мест в очереди): Р0 – вероятность состояния простоя системы, свободной от заявок и Р5 – вероятность состояния трёхканальной системы, занятой обслуживанием трёх заявки в трёх каналах и содержащей две заявки в очереди
Литература
1. Вентцель Е.С. Исследование операций. Задачи, принципы, методология. Учебное пособие. М.: Вузовская книга, 2010. – 192 с.
2. Алиев Т.И. Основы моделирования дискретных систем. СПб.: Изд-во СПбГУ ИТМО, 2009. – 347 с.