BC/NW 2017 № 1 (30):12.1

ПРИМЕНЕНИЕ МЕДОВОГО ШИФРОВАНИЯ К ЧИСЛАМ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ

Зубов И.А

Введение

         Несколько лет назад широкой публике была представлена новая идея в области криптографии, которая при успешном применении позволяет заметно усилить защищённость зашифрованных данных против атак перебором. Обсуждаемая проблема является старейшей и фундаментальной в данной области знаний, но подход к её решению радикально отличается от ранее предложенных. Авторы концепции предложили использовать статистическое кодирование в связке с обычным шифрованием для того, чтобы любая попытка расшифровки данных любым ключом давала бы правдоподобный результат [1]. Это полезно потому, что в этом случае даже после осуществления атаки перебором злоумышленник получает множество правдоподобных вариантов открытого текста, и ему приходится решить дополнительно задачу выделения истинных данных, спрятанных среди множества ложных.

         Поскольку стоит задача максимальной правдоподобности данных, расшифрованных любым ключом, то понятно, что такое шифрование тесно связано с форматом исходных данных. По этой причине медовое шифрование необходимо реализовывать отдельно для каждой предметной области, в которой предполагается его применение. В ходе работы над магистерской диссертацией автор данной статьи уже реализовал примитивы медового шифрования для целых чисел, после чего его внимание переместилось на числа с плавающей запятой.

         1. Формат чисел с плавающей запятой

         Прежде чем говорить об обработке чисел с плавающей запятой, нужно рассмотреть особенности таких чисел.

         В соответствии со стандартом [3] числа с плавающей запятой типов binary32 (обычно соответствует типу float языка C) и binary64 (обычно соответствует типу double языка C) состоят из трёх частей: знакового бита, битов порядка и битов мантиссы. Если знаковый бит равен 0, то число положительно; если 1, то отрицательно.

         Если все биты порядка это нули, то:

         – если все биты мантиссы это нули, то в зависимости от знака число представляет положительный или отрицательный ноль;

         – если не все биты мантиссы это нули, то это денормализованное число, значение которого вычисляется как ( (–1) ^ знак ) * (2 ^ минимально возможный порядок) * 0.мантисса.

         Если все биты порядка это единицы, то:

         – если все биты мантиссы это нули, то в зависимости от знака число представляет положительную или отрицательную бесконечность;

         – если не все биты мантиссы это нули, то это значение типа NaN (not a number, не число), в старшем бите мантиссы которого указано, является ли это значение сигнальным NaN или тихим NaN, в остальных битах мантиссы может передаваться полезная нагрузка. Знак может учитываться или не учитываться в зависимости от реализации. [4]

         Если же биты порядка отличны от случаев «все нули» и «все единицы», то мы имеем дело с нормализованным числом, значение которого вычисляется как ( (–1) ^ знак ) * ( 2 ^ (порядок – минимально возможный порядок – 1) ) * 1.мантисса. [5]

         2. Наивное отображение чисел с плавающей запятой на целые числа

         Итак, вот что мы имеем на данный момент:

         1) Нам очень хотелось бы иметь функции медового шифрования чисел с плавающей запятой, поскольку многие реальные данных хранятся именно в них.

         2) В предыдущем параграфе было показано, что формат чисел с плавающей запятой является достаточно сложным.

         3) С другой стороны, предыдущие работы в области медового шифрования явно показывают, что медовое шифрование можно успешно применить и к более сложным типам данных (см., например, [2, 6]).

         Как же нам поступить, как найти компромисс в этом противоречивом положении? Очевидно, что реализация «в лоб» медового шифрования для таких чисел будет сложной в теоретическом рассмотрении, разработке, отладке и поддержке. Есть ли какой-нибудь обходной путь?

         Мы можем рассмотреть перевод чисел с плавающей запятой в целые числа и обратно. Такой перевод будет очень полезен, поскольку в нашем распоряжении уже есть написанные и отлаженные примитивы медового шифрования для равномерно и произвольно распределённых целых чисел, а разработка эквивалентных по функциональности примитивов медового шифрования для чисел с плавающей запятой требует больших затрат. При нашем подходе для зашифрования чисел с плавающей запятой мы переведём их в целые числа, а затем применим к последним медовое зашифрование целых чисел; для получения исходных значений сначала применим медовое расшифрование целых чисел, а затем переведём последние в исходные числа с плавающей запятой. Большим преимуществом здесь будет максимально общий и не связывающий нам руки алгоритм перевода, который позволит с пользой применять как алгоритмы для равномерно распределённых целых чисел, так и для целых чисел с произвольным законом распределения.

         Все эти размышления приводят к выводу, что конверсия должна осуществляться не произвольным, а каким-то рационально обоснованным образом. Очевидно, для хранения конвертированных чисел будет удобно использовать беззнаковые целые, которые являются несколько более простыми в обработке, чем знаковые. Каким должен быть размер этих целых? Минимально достаточным для того, чтобы сохранить содержимое числа с плавающей запятой (к счастью, тип float языка C имеет тот же размер, что и тип uint32_t – 4 байта; типы double и uint64_t имеют размер 8 байт). Если у нас есть значения с плавающей запятой fp1 и fp2, то после перевода их соответственно в значения int1 и int2 должны выполняться следующие три импликации:

– если fp1 > fp2, то int1 > int2;

         – если fp1 < fp2, то int1 < int2;

         – если fp1 = fp2, то int1 = int2.

Для выполнения этих условий было решено переводить каждое число с плавающей запятой в его номер в последовательности всех возможных чисел с плавающей запятой этого типа. Таким образом, отрицательное число с плавающей запятой, имеющее максимальный порядок и максимальную мантиссу, будет представлено нулём; положительное число с плавающей запятой, имеющее максимальный порядок и максимальную мантиссу, будет представлено максимальным значением соответствующего целочисленного типа. Поскольку размеры типов float и uint32_t, double и uint64_t соответственно равны между собой, то получается, что мы используем всё кодовое пространство целочисленного типа, исключая нежелательные для свойства медовости невозможные значения.

         Для простоты дальнейших рассуждений временно не будем учитывать знаки чисел и согласимся с тем, что после положительной бесконечности могут идти упорядоченные между собой сигнальные NaN-значения, а после них – упорядоченные между собой тихие NaN-значения. Последнее утверждение вполне корректно, поскольку NaN-значения – это вообще не числа, и сравнивать их с числами просто некорректно, о чём сказано в стандарте [4]. В таких условиях доказательство того, что перевод каждого числа с плавающей запятой в его номер в последовательности всех возможных чисел с плавающей запятой этого типа влечёт за собой выполнение трёх импликаций, описанных выше, является тривиальным и для простоты опускается нами в данной статье.

         Мы можем смириться с условием, касающимся редко используемых на практике NaN-значений, однако знаки чисел просто необходимо учесть. Напомним, если знаковый бит числа с плавающей запятой равен 0, то оно положительно, иначе отрицательно. Использование кодового пространства чисел с плавающей запятой представлено в верхней части рис. 1.

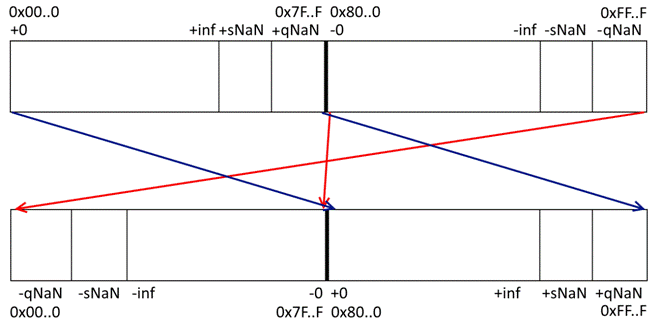Рис. 1. Перевод чисел с плавающей запятой в целые числа

         Итак, как же нам учесть знаки чисел с плавающей запятой, чтобы добиться выполнения трёх импликаций с учётом знаков чисел? Все необходимые для этого преобразования описаны ниже и наглядно показаны на рис. 1: в верхней его части показано кодовое пространство чисел с плавающей запятой, в нижней – пространство целых чисел того же размера, хранящих номера чисел с плавающей запятой в последовательности всех чисел с плавающей запятой данного типа.

         Поскольку положительные числа уже отсортированы в нужном порядке, то их нужно просто переместить из первой половины кодового пространства во вторую для получения их номера: если ielt < 0x80..0, то oelt = ielt + 0x80..0. Для обратного преобразования перемещаем их обратно из второй половины в первую: если oelt >= 0x80..0, то ielt = oelt – 0x80..0. Это показано синими стрелками на рис. 1.

         Отрицательные числа отсортированы в порядке, обратном нужному, поэтому их нужно пересортировать; кроме того, для получения их номеров их нужно переместить из второй половины кодового пространства в первую. Вот как это можно сделать: если ielt >= 0x80..0, то oelt = 0xFF..F – ielt = ~ielt, где символ «~» означает побитовую инверсию. Для обратного преобразования перемещаем их обратно из первой половины во вторую, пересортируя их в обратном порядке: если oelt < 0x80..0, то ielt = 0xFF..F – oelt = ~oelt. Это показано красными стрелками на рис. 1.

         Что нам даёт такое кодирование? К сожалению, совсем немного. Дело в том, что числа с плавающей запятой имеют довольно сложный закон распределения. Они распределены равномерно внутри интервалов, имеющих одинаковый порядок. Более конкретно, они распределены равномерно внутри интервалов, входящих в:

         1) любой из интервалов вида [-2^(e+1); -2^e] или [2^e; 2^(e+1)], где e = (порядок + минимально возможный порядок – 1), порядок имеет допустимое значение для данного типа, но не состоит в двоичном представлении из одних нулей (денормализованные числа, положительный и отрицательный нули) или из одних единиц (NaN-значения, положительная и отрицательная бесконечности);

         2) интервал [-2^(e+1); -0] или интервал [+0; 2^(e+1)], где e – минимально возможный порядок;

         3) интервал, содержащий все отрицательные сигнальные NaN-значения;

         4) интервал, содержащий все положительные сигнальные NaN-значения;

         5) интервал, содержащий все отрицательные тихие NaN-значения;

         6) интервал, содержащий все положительные тихие NaN-значения.

         При этом перечисленные выше интервалы в общем случае имеют различную длину (рис. 2), в чём и заключается главная проблема для нас.

         Получается, что после применения алгоритма конверсии мы можем эффективно использовать примитивы медового шифрования равномерно распределённых целых чисел только в том случае, если исходные равномерно распределённые числа с плавающей запятой целиком лежат в одном из интервалов, перечисленных выше! Теоретически мы могли бы использовать более широкие интервалы, вплоть до [-inf; +inf], если бы исходные числа с плавающей запятой были бы распределены равномерно по множеству представимых чисел с плавающей запятой, но этот случай представляется автору крайне маловероятным. Вывод таков: для решения задачи необходимо разработать более сложный и практичный алгоритм.

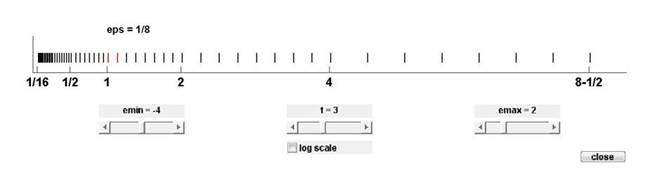Рис. 2. Распределение чисел с плавающей запятой [8]

         3. Наброски усложнённого алгоритма

         Для большей наглядности дальнейших рассуждений перейдём от рассмотрения конкретных типов с плавающей запятой к упрощённому примеру. Пусть у нас имеется некоторый тип с плавающей запятой, который может хранить следующие значения:

         – тихие NaN-значения с полезной нагрузкой -3, -2, -1, -0;

         – сигнальные NaN-значения с полезной нагрузкой -3, -2, -1;

         – отрицательная бесконечность -inf;

         – нормализованные числа -7, -6, -5, -4, -3.5, -3, -2.5,  -2, -1.75, -1.5, -1.25, -1;

         – денормализованные числа -0.75, -0.5, -0.25;

         – отрицательный и положительный нули -0, +0;

         – денормализованные числа 0.25, 0.5, 0.75;

         – нормализованные числа 1, 1.25, 1.5, 1.75, 2, 2.5, 3, 3.5, 4, 5, 6, 7;

         – положительная бесконечность +inf;

         – сигнальные NaN-значения с полезной нагрузкой 1, 2, 3;

         – тихие NaN-значения с полезной нагрузкой +0, 1, 2, 3.

         Подобным образом распределены и допустимые значения реальных типов с плавающей запятой float и double, что и делает такое упрощение достаточно реалистичным для нас.

         Что мы можем увидеть на этом примере? В множестве представимых нормализованных чисел можно выделить интервалы, на которых шаг между двумя соседними значениями остаётся постоянным: [-7; -4] (шаг 1), [-4; -2] (шаг 0.5), [-2; -1] (шаг 0.25), [1; 2] (шаг 0.25), [2; 4] (шаг 0.5), [4; 7] (шаг 1). То же самое касается и денормализованных чисел, в которых можно выделить следующие интервалы: [-0.75; -0] (шаг 0.25) и [+0; 0.75] (шаг 0.25).  Обратите внимание, что шаг в денормализованных интервалах равен наименьшему шагу, встречающемуся в нормализованных числах: в общем и целом шаг остаётся постоянным на интервалах [-7; -4] (шаг 1), [-4; -2] (шаг 0.5), [-2; -0] (шаг 0.25), [+0; 2] (шаг 0.25), [2; 4] (шаг 0.5), [4; 7] (шаг 1). Постоянным является и шаг полезной нагрузки NaN-значений: он равен 1 на всём множестве возможных значений полезной нагрузки, то есть на интервалах [-3; -1] и [1; 3] для сигнальных NaN-значений, [-3; -0] и [+0; 3] для тихих.

         Как уже отмечалось ранее, на интервалах с равным шагом распределение значений будет фактически равномерным, так что описанное выше отображение чисел с плавающей запятой на целые числа будет отлично работать. Округление будет вносить небольшое отклонение от по-настоящему равномерного распределения, но его значением можно пренебречь. Более конкретно, для двоичных чисел с плавающей запятой, которые мы рассматриваем, вариантом округления по умолчанию в стандарте IEEE 754 является так называемое «банковское» [3]. Оно подразумевает, что если число находится между двумя представимыми значениями, то оно округляется к тому из них, которое является чётным. Простой и чисто иллюстративный пример такого округления для десятичных чисел: значения +23.5 и +24.5 округляются до +24, в значения −23.5 и −24.5 округляются до −24 [9].

         А что, если мы хотим отобразить массив чисел с плавающей запятой из другого интервала, например,  [1.5; 2.5]? Представимыми значениями на этом интервале являются числа 1.5, 1.75, 2, 2.5. Если мы закодируем их по наивному алгоритму выше, то эти четыре значения будут встречаться с одинаковой вероятностью. Это звучит парадоксально, но такое распределение не будет соответствовать равномерному распределению чисел на интервале [1.5; 2.5]! Легко увидеть, что если бы точность чисел с плавающей запятой была бы равной нашему шагу 0.25, то следующие 5 значений встречались бы с одинаковой вероятностью: 1.5, 1.75, 2, 2.25, 2.5. Проблема заключается в том, что значение 2.25 не представимо в явном виде, так что примерно половина чисел, которые могли быть округлены в это значение, будет округлены в 2, а ещё примерно половина – в 2.5. Слово «примерно» в предыдущем предложении вызвано тем, что точное значение 2.25 будет всегда округляться либо в 2, либо в 2.5, что вызовет небольшую неравномерность в таком округлении. Таким образом, каждое из чисел 1.5 и 1.75 встречается с вероятностью x, каждое из чисел 2 и 2.5 – с вероятностью 1.5x.

         А как насчёт отображения чисел из интервала [1.5; 3]? Непредставимыми здесь будут значения 2.25 и 2.75, вероятности которых поделятся примерно пополам между представимыми значениями 2 и 2.5, 2.5 и 3 соответственно. Таким образом, каждое из чисел 1.5 и 1.75 встречается с вероятностью x, каждое из чисел 2 и 3 – с вероятностью 1.5x, число 2.5 – с вероятностью 2x.

         С расширением интервала всё становится ещё сложнее. На интервале [1.5; 5] непредставимыми являются значения 2.25, 2.75, 3.25, 3.75, 4.25, 4.5, 4.75. С распределением вероятностей первых четырёх значений ситуация будет такой же, как и раньше. Все значения, которые могли бы округляться в 4.25 при точности чисел с плавающей запятой, равной нашему шагу 0.25, теперь будут округляться в 4;  все значения, которые могли бы округляться в 4.75, теперь будут округляться в 5. Вероятность числа 4.5 поделится примерно пополам между представимыми значениями 4 и 5. Итого: вероятность каждого из чисел 1.5 и 1.75 – x, числа 2 – 1.5x (вероятность значения 2, половина вероятности значения 2.25), каждого из чисел 2.5, 3, 3.5 – 2x, числа 4 – 3x (вероятность значений 4 и 4.25, половины вероятностей значений 3.75 и 4.5),  числа 5 – 2.5x (вероятность значений 5 и 4.75, половина вероятности значения 4.5).

         Отдельно стоит рассмотреть ситуацию с положительным и отрицательным нулями. Для обеспечения равномерности распределения после перевода в целые числа следует поступить так: если интервал содержит только отрицательный или только положительный ноль, то этому значению следует присвоить ту же вероятность, что и любому денормализованному числу; если же интервал содержит оба нуля, то каждому из них следует присвоить вероятность, равную половине вероятности денормализованного числа. Такой подход имеет следующее обоснование. Шаг между двумя соседними денормализованными числами одного знака всегда остаётся постоянным (см. представленную ранее формулу). Если мы попробуем найти число, которое будет на расстояние шага ближе к нулю, чем наибольшее представимое отрицательное денормализованное число или наименьшее представимое положительное денормализованное число, то мы в обоих случаях получим ноль. Кроме того, в стандарте IEEE 754 сказано, что численное сравнение отрицательного и положительного нулей должно выдавать результат «числа равны» [7], а для большинства задач можно считать два этих значения равными друг другу. Таким образом, если внутри интервала содержатся два разных нуля, то будем считать их просто двумя разными кодовыми значениями, представляющих одно и то же число. Каждому NaN-значению (если такие значения входят в интервал) можно присвоить минимальную представимую вероятность, так как такие значения встречаются сравнительно редко. Обрабатывать NaN-значения нужно очень аккуратно, так как результатом любых сравнений с ними является «ложь» [4].

         А как нам поступить с положительной и отрицательной бесконечностями? Логика авторов стандарта IEEE вполне понятна при рассмотрении нашего простого типа: вообще-то следующим представимым числом после 7 должно было стать число 8, но поскольку мы не можем представить в нашем типе все последующие числа, то давайте объединим в понятии «положительная бесконечность» число 8 и все последующие. Отсюда вытекает прагматичное решение: в наших расчётах мы можем принять, что никаких бесконечностей нет, есть лишь заменяющие их представимые значения (-8 вместо -inf и 8 вместо +inf). Это позволит нам избежать учёта данной ситуации как особой при программировании, поскольку тогда случай интервала, например, [6; +inf] концептуально не отличается от случая интервала [1; 2]. Насколько обоснованным будет такое допущение? Значения -inf и +inf должны сравнительно редко встречаться на практике, что несколько смягчает остроту вопроса. Тем не менее, если такое значение появляется где-то в исходных, промежуточных или результирующих данных, то оно с большой вероятностью может появиться и где-то ещё в этом же наборе данных. Это вызвано тем, что значительное число математических операций с бесконечностями (скажем, сложение +inf и 1) приведёт к бесконечностям. Другими словами, это редкие значения, но если они всё же появляются, то целыми группами. В таких условиях наше допущение можно назвать достаточно правдоподобным, поскольку предыдущие рассуждения показывают – вес бесконечностей при таком рассмотрении окажется сравнительно крупным, но не чрезмерно. Если же бесконечности вообще не фигурировали в допустимых значениях исходных данных, их не будет и при расшифровке неверным ключом. Словом, такой подход к проблеме видится вполне удовлетворительным.

         Отобразить описанные выше различия вероятностей в кодовом пространстве будет несложно, поскольку ранее автором данной статьи была решена ровно эта задача: кодирование произвольно распределённых целых чисел при наличии их весов. С другой стороны, выше было показано, что нахождение нужных весов для конкретных значений является весьма непростой задачей. Автор данной статьи оставляет этот вопрос открытым для будущих исследований.

Литература

         1. A. Juels, T. Ristenpart. Honey Encryption: Security Beyond the Brute-Force Bound. EUROCRYPT, pp. 293-310, 2014.

https://eprint.iacr.org/2014/155.pdf

         2. Marc Beunardeau, Houda Ferradi, Rémi Géraud, David Naccache. Honey Encryption for Language. IACR Cryptology ePrint Archive 2017: 31 (2017).

https://eprint.iacr.org/2017/031.pdf

         3.  IEEE floating point

https://en.wikipedia.org/wiki/IEEE_floating_point

         4.  NaN

https://en.wikipedia.org/wiki/NaN

5. Single-precision floating-point format

https://en.wikipedia.org/wiki/Single-precision_floating-point_format

6. Zhicong Huang, Erman Ayday, Jacques Fellay, Jean-Pierre Hubaux, Ari Juels. GenoGuard: Protecting Genomic Data against Brute-Force Attacks. IEEE Symposium on Security and Privacy (SP), pp. 447-462, 2015.

https://infoscience.epfl.ch/record/205068/files/main.pdf

         7. Signed zero

https://en.wikipedia.org/wiki/Signed_zero

         8. Cleve Moler. Floating Point Numbers

http://blogs.mathworks.com/cleve/2014/07/07/floating-point-numbers

         9. Rounding

https://en.wikipedia.org/wiki/Rounding