BC/NW 2017 № 1 (30):12.5

ПРИМЕНЕНИЕ УНИВЕРСАЛЬНЫХ ПРЕДСТАВЛЕНИЙ ЧИСЕЛ ДЛЯ РЕШЕНИЯ ЗАДАЧ ВЫЧИСЛИТЕЛЬНОЙ ГЕОМЕТРИИ

Ермилов С.И., Оцоков Ш.А.

Проблема достоверных вычислений является актуальным направлением в области теоретической информатики вследствие большого объема научных и инженерных задачах [1].

Одной из таких проблем является решение задач вычислительной геометрии, например, построение выпуклой оболочки. Задачи вычислительной геометрии используется в распознавании образов, машинной графике, инженерном проектировании и т. д.

Универсальное представление числа (УПЧ) — это множество объектов {s,e,m,u,es,fs}, где s — знак числа, равный нулю или единице; e — порядок числа со знаком; m — мантисса без знака; u — бит неопределенности; es — размер экспоненты в битах; fs — размер мантиссы в битах.

Введение дополнительных бит расширяет поле возможных значений формата, объединяя в едином формате возможности чисел с плавающей точкой и интервальной арифметики [2]. Арифметические операции определяются в формате с плавающей точкой, но в случае обнаружения округления числа за счет бита округления значение переходит в достоверный интервал, и дальнейшие вычисления ведутся с интервалами. Преимуществом УПЧ является устранение ошибок округления с помощью встроенного механизма интервальной арифметики.

Самым простым методом для построения выпуклой оболочки множества точек является алгоритм быстрой оболочки. Однако алгоритм вычислительно неустойчив из-за недостатков чисел с плавающей точкой, например, при наличии в исходном множестве близких друг к другу точек.

Для оценки результатов используется следующий эксперимент. Сгенерируем множество точек для построения выпуклой оболочки, найдем оболочки тремя способами: на основе чисел с плавающей точкой, интервальной арифметики и УПЧ и сравним полученные результаты с эталонным, вычисленным заранее.

 

Литература

1. Bailey D.H. High-precision floating-point arithmetic in scientific computation//Computing in science & engineering. 2005. Vol. 7. No 3. С. 54—61.

2. Gustafson J.L. The End of Error. Unum Computing. 2015.

 

ПРИМЕНЕНИЕ УНИВЕРСАЛЬНЫХ ЧИСЛОВЫХ ПРЕДСТАВЛЕНИЙ ДЛЯ ЗАДАЧ ВЫЧИСЛИТЕЛЬНОЙ ГЕОМЕТРИИ

Ермилов С.И. ВМСС ermilov_s@mail.ru

 

Виды машинных арифметик

•      Целочисленная арифметика

•      Формат с плавающей точкой (IEEE 754)

•      Интервальная арифметика (IEEE 1788)

•      Универсальные числовые представления (Unum)

 

Недостатки стандарта IEEE 754

•      Неравномерное распределение чисел

•      Погрешность из-за округления чисел

•      Нарушение законов алгебры

•      Зависимость от реализации стандарта

 

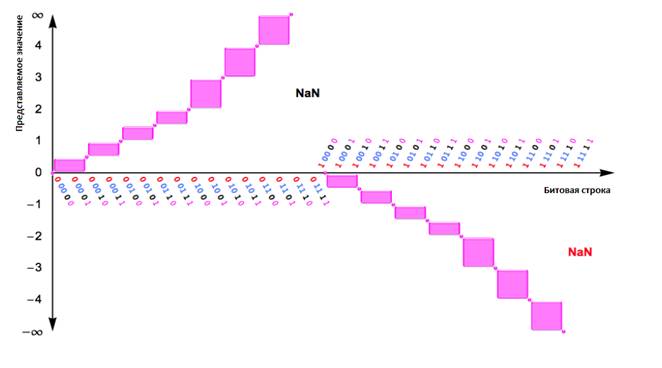
Универсальный числовой формат (Unum)

•      Знак, порядок, мантисса определяют число с плавающей точкой

•      Бит неопределенности: u = 0 - число точное, u = 1 – интервал от текущего значения до след. числа ( a; a + ULP);

•      Размер порядка и размер мантиссы используются для автоматического контроля

 

Универсальный числовой формат (Unum)

 

Достоинства Unum

•      Отсутствие ошибок округления, переполнения и потери значимости

•      Покрытие всего множества действительных чисел

•      Варьируемая размерность экспоненты и мантиссы ( в перспективе уменьшение пропускной способности памяти  и энергопотребления)

 

Недостатки Unum

•      Более сложная логика обработки по сравнению с числами с плавающей точкой

•      Переменный размер представляемых чисел ( проблемы с хранением в памяти

Определение выпуклой оболочки

Определение выпуклой оболочки

https://upload.wikimedia.org/wikipedia/commons/thumb/d/de/ConvexHull.svg/220px-ConvexHull.svg.png

 

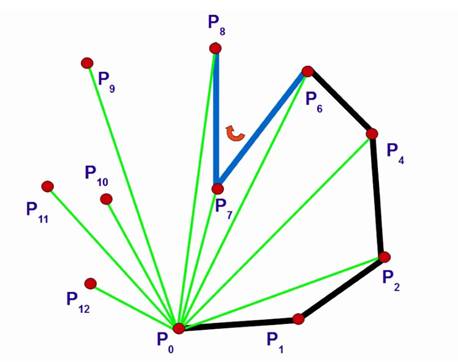
Алгоритм Грэхема

•      Построение В.О. через сравнение углов между точками

•      Уязвимое место – определение ориентирования точек.

 

Алгоритм Грэхема с Unum

•      Легко определить некорректность работы алгоритма

•      Возможность получения зон «неопределености»

•      Автоматический подбор точности

 

Некорректное построение В.О.

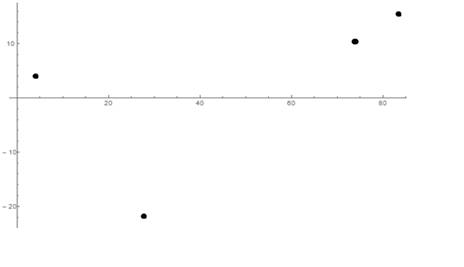
Исходные данные:

{{4.0,4.0},

{27.6435643564…, -21.88118811881…},

{73.4158415841…,     8.86138613861…},

{83.3663366336…,   15.54455445544… }}

 

 

Некорректное построение В.О.

 

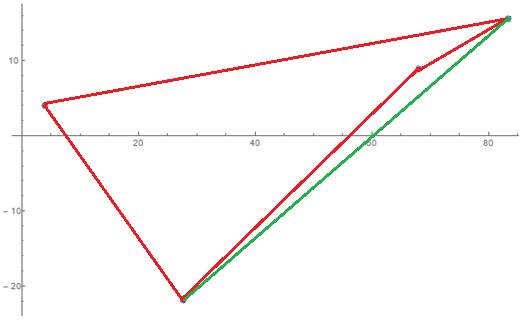
Корректный результат:

X = {p1,p2,p4}.

При расчетах с типом double:

X = {p1,p2,p3,p4}

При расчетах с unum:

X = {p1,p2,p4}

 

 

Заключение

•      Числа с плавающей точкой не всегда могут обеспечить достоверность полученных результатов

•      Unum позволяет получить достоверные результаты за счет дополнительной логики

•      Необходима разработка процессора с поддержкой Unum