BC/NW 2017 № 2 (31);7.1

АЛГОРИТМ БЫСТРОГО ВЫЧИСЛЕНИЯ ПОКАЗАТЕЛЬНЫХ ФУНКЦИЙ

Мачарадзе Г.Т., Морозова Е.А., Раскатова М.В.

Введение

         При разработке систем реального времени бывают случаи, когда алгоритм не успевает завершиться за период обновления данных. В таких случаях необходимо искать способы оптимизации алгоритма обработки данных, чтобы ускорить время выполнения.

Примером такой системы могут быть 3D-системы. Для расчета таких параметров как освещение, отражение используется огромное количество нормалей поверхностей. Нормаль – вектор единичной длины, перпендикулярный данной поверхности. Чтобы нормализовать вектор (т.е. сделать единичной длины), необходимо вектор умножить на величину:. Ускорив операцию вычисления обратного корня, можно существенно ускорить обработку данных, поскольку извлечение квадратного корня занимает очень много машинного времени.

 Алгоритм быстрого вычисления обратного квадратного корня был разработан в 1990-х годах компанией Silicon Graphics, а реализация впервые появилась в исходном коде компьютерной игры Quake III.

         Целью данной статьи состоит в обобщении алгоритма для быстрого вычисления функций вида , а также в сравнении временных характеристик алгоритма быстрого вычисления с алгоритмом, использующим стандартные функции, что позволит сделать вывод о пригодности данного алгоритма на современных быстродействующих процессорах.

Некоторые сведения о числах с плавающей точкой

В ЭВМ вещественные числа представляются в формате IEEE754, согласно которому число представляется в виде бита знака, смещенного порядка и мантиссы. Для одинарной точности представления (соответствует типу float в языке C) справедливо следующее:

Формула для перехода из IEEE754 к десятичному формату:

(1) 

Например, для десятичного числа 12.75 имеем:

.

Если интерпретировать порядок и мантиссу числа x как целые числа, то целочисленное представление числа x можно записать в виде

                                                                  (2)

Математическое обоснование алгоритма

Пусть необходимо вычислить значение функции:

Прологарифмируем обе части равенства по основанию 2:

Заменим x и y, используя выражение (1):

 Упрости выражение, раскрыв логарифм произведения:

                             (3)

Рассмотрим функцию . В нашем случае мантисса нормализована, т.е. справедливо неравенство: . На полуинтервале [0, 1) функция g(m) примерно ведет себя как линейная функция . Меняя параметр , мы можем улучшить точность приближения.      дает лучшее приближение.

Таким образом, можно записать:

                                           (4)

Преобразуем (3), используя (4):

Перейдем от e, m к E, M по равенствам, указанным в (1):

Умножим обе части равенства на L и перенесем все слагаемые, несвязанные с y в правую часть равенства:

Используя (2), получим:

             (5)

Значение  выбрано не просто так. Такой выбор позволяет заменить операцию умножения на сдвиг числа вправо или влево, в зависимости от знака p.  Таким образом, целочисленную интерпретацию результата можно получить, сдвинув аргумент функции на k разрядов (вправо/влево) и прибавив константу.  Данное приближение дает точность порядка 4%. Повысить точность можно с помощью метода Ньютона.

Рассчитаем значение константы из выражения (5) при :

Уточнение результата методом Ньютона

Формула для следующего приближения имеет следующий вид:

                                                     (6)

Применим данный метод для функции ;

Подставив производную в (6), получим формулу для второго приближения результата:

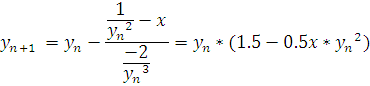
Данное уточнение повышает точность результата до 0.18%.

Реализация алгоритма вычисления обратного квадратного корня на языке C

inline float Q_Sqrt_Inverse(float x) {

const float half = 0.5f * x; //запоминаем половину для последующей аппроксимации

         int y = * (int *)&x; //приводим к int

         y = 0x5F3759DF - (y >> 1); //вычисляем первое приближение

         x = * (float *)&y; //приводим к float

         x = x * (1.5f - (half * x * x)); //аппроксимация метода Ньютона

         return x;

}

В таблице 1 приведены полученные времена выполнения функции по сравнению с функциями, использующих стандартные математические функции sqrt и sqrtf.

Таблица 1

Время выполнения функций

	sqrt	sqrtf	Q_Sqrt_Inverse
Без уточнения результата	0.170480	0.140246	0.060292
С уточнением результата	0.170480	0.140246	0.083915

В таблице 2 приведены коэффициенты ускорения приведенного алгоритма по отношению к стандартным функциям sqrt и sqrtf.

Таблица 2

Коэффициенты ускорения алгоритма по отношению к стандартным функциям

	Ускорение относительно sqrt	Ускорение относительно sqrtf
Без уточнения результата	2.83	2.33
С уточнением результата	2.03	1.67

Заключение

Анализируя полученные данные, можно с уверенностью заявить, что в настоящее время даже с учетом существования блоков FPU (Floating Point Unit), которые на аппаратном уровне реализуют операции с плавающей точкой, приведенный алгоритм все еще может использоваться по назначению. При точности 0.2% можно получить ускорение данной операции минимум на 50%.

Литература

1. Fast inverse square root – URL: https://en.wikipedia.org/wiki/Fast_inverse_square_root

2. А.А.Амосов, Ю.А.Дубинский, Н.В. Копченова – Вычислительные методы. Издательство Лань, 2014 год.