BC/NW 2018 № 2 (33):4.2

 

ПРОГРАММНАЯ РЕАЛИЗАЦИЯ  МОДУЛЯ ДИСПЕТЧЕРИЗАЦИИ  ВНЕШНИХ ЗАПРОСОВ  В КОМПЬЮТЕРНОЙ СЕТИ

Данилин Г.Г., Манов А.С.

 

Проектирование и реализация любой сетевой структуры предполагает, в конечном счёте, закупку дорогостоящего (а зачастую и многочисленного) сетевого оборудования. При отсутствии точных данных о количестве требуемой техники, у предприятия есть риск избыточных экономических затрат при покупке лишнего оборудования, которое потенциально будет находиться в простое. Или же, наоборот, недостаток требуемой аппаратной базы скажется на работоспособности и общему функционалу всей сети предприятия.

Для решения вышестоящей проблемы в современных сетевых структурах используют принципы и механизмы компьютерного моделирования. Это обусловлено возможностью без существенных затрат проанализировать и оценить необходимые параметры проектируемой сети непосредственно на этапе планирования.

     В данной работе рассматривается моделирование только малой части сети — модуля диспетчеризации. Он состоит из коммутатора, который принимает входной поток пакетов и передает эти пакеты на нужный сервер. Проводится имитационное моделирование с помощью созданной на языке C#  программы. По результатам имитационного моделирования строится зависимость количества серверов от плотности (времени между поступившими друг за другом заявками) входного потока. 

 

                                Создание модели сети

 

            Для создания  модели требуется перейти от структурной схемы модуля диспетчеризации к схеме аналитического моделирования.

Схема рассматриваемой сети представлена на рис. 1.

Рис. 1. Схема рассматриваемой сети

Описать рассматриваемую систему можно следующим образом. Существует n параллельных идентичных серверов и очередь из m мест. На вход коммутатора поступает k простейших потоков с интенсивностями . Поток, получаемый в результате суперпозиции этих потоков, тоже будет простейшим с интенсивностью

(1)
 
,

 

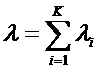где — суммарный поток.

Время обслуживания заявки на сервере имеет показательное распределение с показателем . Пакет, пришедший на модуль диспетчеризации и заставший хотя бы один сервер свободным, сразу же занимает любой из свободных  серверов, где начинается процесс его обслуживания. В случае, если все сервера в момент поступления пакета заняты, он помещается в очередь. Из очереди пакеты выбираются на обслуживание в соответствие с дисциплиной FIFO (первый пришедший пакет будет обслужен первым освободившимся сервером). Заявка, заставшая все сервера и все места в очереди занятыми, навсегда покидает систему, не оказывая никакого влияния на ее дальнейшее функционирование.

        Разработка алгоритма имитационного  моделирования

 

Возвращаясь к теме данной работы, стоит еще раз упомянуть, что для моделирования СМО с случайными распределениями потоков заявок и потоков обслуживания применяется метод имитационного моделирования по событиям. Событиями в СМО являются моменты времени, когда очередная заявка приходит в систему и когда обслуженная заявка покидает систему. Иначе говоря, это моменты изменения состояния системы. Эти моменты образуют совокупность событий, в которой можно выделить текущее событие и множества прошедших и будущих событий. Метод имитационного моделирования включает последовательное формирование списка событий и продвижение процесса моделирования от одного события к другому. Модельное время при имитационном моделировании является зависимой переменной и изменяется скачками, равными интервалам времени между последовательными событиями. 

В рамках данной работы было разработано два алгоритма. Первый алгоритм — это алгоритм имитационного моделирования модуля диспетчеризации внешних запросов в сети. Второй алгоритм — это алгоритм определения зависимости необходимого количества серверов от времени между поступающими друг за другом заявками.

 

        Функции имитационной модели

 

На основе аналитической модели рассматриваемой сети, для дальнейшей программной реализации, опишем имитационную модель и её функции.

На рис. 2. приведена схема имитационной модели.

 

 

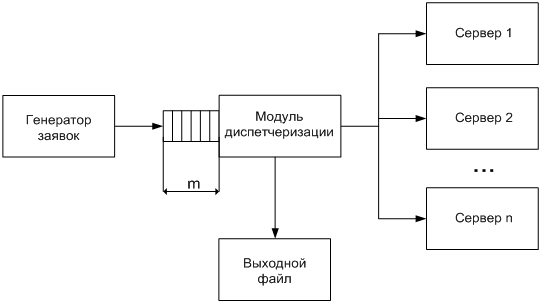
Рис. 2. Схема имитационной модели

 

Данная модель выполняет описанные ниже функции:

а)                               Имитируется поток входных заявок, распределенный по экспоненциальному закону. Параметры закона распределения: математическое ожидание и дисперсия, задаются пользователем.

б)                              Заявки попадают на вход модуля диспетчеризации, который распределяет их по  серверам.

в)                               Результат фиксируется в выходном файле, который должен содержать следующую информацию:

1)                          количество серверов в узле;

2)                          среднюю загрузку каждого сервера, в процентах от общего

              времени работы сервера;

3)                          количество превышений загрузки над пропускной

              способностью для каждого сервера.

г)                               По результатам моделирования будет построена зависимость количества необходимых серверов от времени между поступающими друг за другом заявками. Таким образом можно оценить аппаратные затраты, необходимые для обслуживания клиентов для различной интенсивности их работы.

 

        

                      Алгоритм работы имитационной модели

 

Используя концепции моделирования по событиям, опишем алгоритм имитационного моделирования модуля диспетчеризации внешних запросов в сети (схема  алгоритма представлена па Рис.3).

 

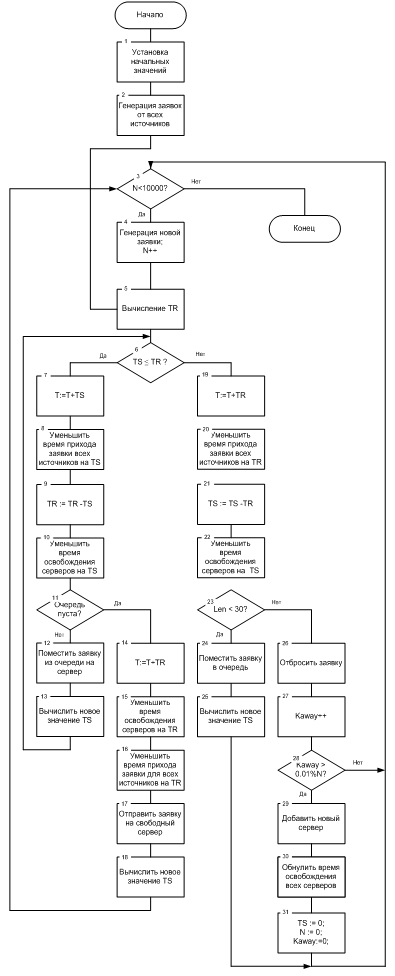
Рис.3.Схема алгоритма  работы имитационной модели

Принятые обозначения:

·                   N — общее количество пришедших в систему заявок;

·                   T — текущее модельное время, изменяющееся скачком между

           моментами возникновения событий в системе;

·                   TR — минимальное время, через которое поступит следующая заявка;

·                   TS — минимальное время, через которое освободится сервер;

·                   Kaway — количество заявок, покинувших систему;

·                   Len — длина очереди.

В процессе моделирования в любой момент времени известны моменты наступления событий для всех возможных источников (момент прихода очередной заявки и моменты освобождения каждого из серверов). Если сервер свободен, то ожидаемое время его освобождения принимается равным нулю.

Во избежание возникновения бесконечного цикла в программе установлено ограничение: если обработано 10000 заявок, и при этом число заявок, покинувших систему, не превысило 0,01% от общего числа заявок, то моделирование заканчивается.

Установка начальных значений (блок 1) состоит в создании массива для заявок, для источников, обнулении значений N, len, Kaway, TR, TS.

Генерация заявок от всех источников (блок 2) состоит в заполнении массива Clients временами прихода заявок относительно текущего момента времени. Генерация времени происходит при помощи генератора псевдослучайных чисел и преобразования Бокса-Мюллера (метод получения нормально распределённых чисел в отрезке [0;1]).

В блоке 5 определяется момент прихода очередной заявки, при этом модельное время не изменяется.

В блоке 3 осуществляется проверка условия окончания моделирования.

В блоке 4 происходит генерация новой заявки для того источника, чья заявка была обработана в процессе работы программы.

Блок 6 реализует проверку, какое событие произойдет раньше: придет заявка в момент времени TR или освободится сервер в момент TS. При начальном запуске эти времена равны нулю. Если сервер освободится раньше, или время освобождения сервера равно времени прихода заявки (TR ≤ TS), то происходит переход к блоку 7. Если же все сервера будут заняты, когда придет заявка (TS > TR), то происходит переход к блоку 17.

Блок 7 осуществляет скачок модельного времени в момент наступившего события — освобождения сервера.

Поскольку произошло изменения модельного времени, необходимо все параметры системы привести к этому времени. В 8, 9 и 10 блоках осуществляется «приближение» времени прихода заявок от всех источников, а также время освобождения всех серверов на величину TS.

Так как наступил момент освобождения сервера, а новая заявка еще не пришла, необходимо произвести проверку, есть ли заявки в очереди (блок 11).

Если очередь не пуста, то происходит переход на блок 12, заявка из очереди помещается на обработку на освободившийся сервер. Блок 13 реализует вычисление нового значения TS — из массива времен освобождения всех серверов выбирается минимальное время, оно и становится новым значением TS. Происходит возврат на сравнение времен TR и TS.

Если же очередь пуста, то на освободившийся сервер не может поступить никакая заявка, и система должна ожидать прихода новой заявки. Поэтому происходит переход в момент прихода заявки (блок 14). Далее осуществляется «приближение» времени прихода заявок от всех источников, а также время освобождения всех серверов на величину TR (блоки 15 и 16), а заявка отправляется на свободный сервер (блок 17). Блок 18 аналогичен блоку 13, в нем вычисляется новое значение TS. Далее цикл, начиная с блока 3, начинается вновь.

Рассмотрим теперь вариант, когда заявка приходит в систему раньше, чем освобождается сервер (ветвь «нет» блока 6). В этом случае происходит переход на время прихода заявки (блок 19). Блоки 20-22 реализуют ту же логику, что и блоки 8-10. Далее осуществляется проверка очереди (блок 23).

Если очередь еще не достигла максимальной длины (в ней меньше 30 заявок), то заявка помещается в очередь (блок 24), вычисляется новое значение TS (блок 25, аналогичен блоку 13).

Если же очередь уже достигла максимальной длины (30 заявок), то пришедшая заявка покидает систему, не оказав на нее никакого влияния (блок 26), увеличивается счетчик отброшенных заявок (блок 27),  далее производится проверка условия добавления нового сервера в систему (блок 28). Если отброшено более 0.01% всех заявок, пришедших в систему, то будет добавлен новый сервер (блок 29), а также в блоках 30-31 обнулены все счетчики (общее количество заявок,  количество заявок, покинувших систему, времена освобождения серверов).

После блоков 25, 31, а также по ветви «Нет» блока 28 происходит переход на блок 3 — условие окончания моделирования.

(2)
 
По окончании моделирования считается среднее время между заявками:

Средняя загрузка серверов (для каждого сервера) считается как отношение времени занятости каждого сервера к общему модельному времени T.

 

        Алгоритм определения необходимого количества серверов

 

Схема алгоритма определения необходимого количества серверов приведена на Рис.4. Данный алгоритм используют те же обозначения, что и в предыдущем.

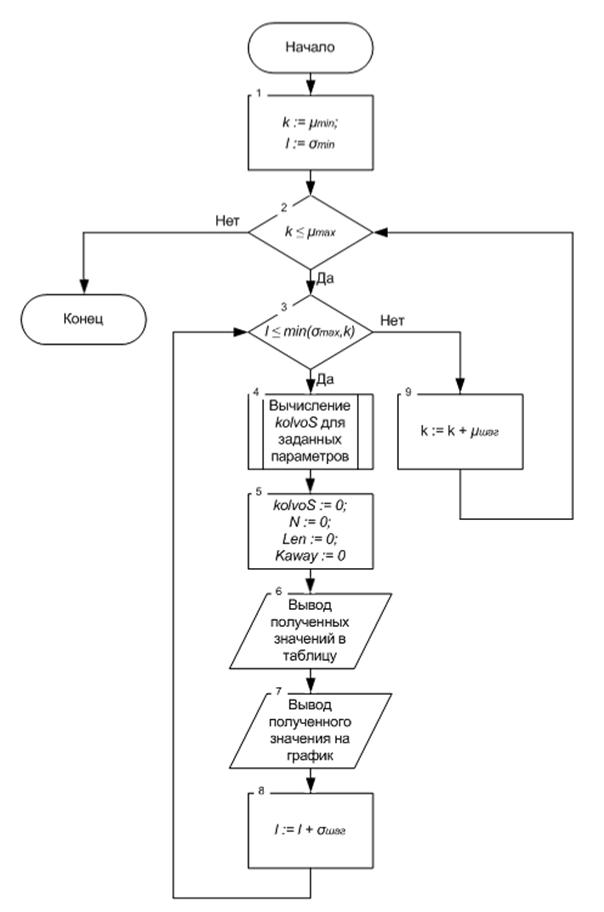
       Рис.4 Алгоритм определения количества серверов

Однако стоит упомянуть об некоторых новых переменных, а именно

 

·                   k — переменная цикла, принимающая значения математического

          ожидания из заданного диапазона;

·                   l — переменная цикла, принимающая значения среднеквадратичного

          отклонения из заданного диапазона;

·                   μmin,  μmax — минимальное и максимальное значение математического

          ожидания соответственно;

·                   σmin, σmax — минимальное и максимальное значение

          среднеквадратичного отклонения соответственно;

·                   μшаг, σшаг — значения шага для математического ожидания и

                    среднеквадратичного отклонения.

В блоке 1 происходит инициализация переменных цикла k и l. Им присваиваются значения, равные нижним границам заданных диапазонов математического ожидания и среднеквадратичного отклонения.

В блоке 2 происходит проверка на достижение переменной k значения верхней границы диапазона μmax. Если значение не было достигнуто, то происходит переход на блок 3, в котором происходит аналогичная проверка для переменной l. Но для этой переменной введены изменения. Дело в том, что верхняя граница диапазона среднеквадратичных отклонений может оказаться намного больше, чем текущее значение математического ожидания, для которого производится моделирование. Для этого было введено ограничение: значение среднеквадратичного отклонения не может быть больше, чем значение математического ожидания. Т.е. цикл будет закончен в том случае, если переменная l должна достигнуть значения min(σmax,k).

Если переменная k еще не достигла верхней границы диапазона, начинается моделирование, происходит переход к блоку 4. Этот блок содержит вычисление необходимого количества серверов для текущих значений k (математического ожидания) и l (среднеквадратичного отклонения). На выходе этого блока формируется численное значение необходимого количества серверов для заданной конфигурации узла.

Для дальнейшей работы программы происходит обнуление значений kolvoS, N, Len, Kaway. Это реализуется в блоке 5. Следующим шагом происходит переход на блоки 6 и 7, в которых осуществляется вывод полученных значений на экран. Сначала они записываются в массив (блок 6), а потом генерируется точка на графике (блок 7). В 8 блоке переменная  l увеличивается на значение σшаг, после чего происходит возврат на блок 3.

При окончании цикла по переменной l (l примет значение больше σmax), происходит возврат во внешний цикл (по переменной k), в блоке 9 переменная  k увеличивается на значение, равное μшаг, после чего происходит возврат на блок 2. Когда закончится и этот цикл (k примет значение больше μmax), моделирование окончено. Происходит выход из программы.

Разработанные алгоритмы  реализованы на языке C#. Выбор обусловлен возможностью организации доступного пользовательского интерфейса. Средой разработки программного обеспечения выберем Microsoft Visual Studio 2015 со встроенными библиотеками.

Ниже  приведён список основных функций, участвующих в реализации алгоритма.

·                   public static double BoksMul(Random rnd) – функция распределения Бокса-Мюллера, генерация случайной величины времени обработки заявки сервером;

·                   public void Grapth(List<double> Clients,int n, Chart SS) – функция отрисовки графика в координатах X-Y;

·                   public int Ochered (Random rnd, int n) – функция формирования очереди заявок;

·                   public static double Expon(double x, double time) – экспоненциальный закон для входного потока заявок;

·                   private void button1_Click(object sender, EventArgs e) – функция, осуществляющая алгоритм работы имитационной модели (основные параметры: N - общее кол-во заявок, T - текущее время моделирования, TR - минимальное время до следующей заявки, TS - минимальное время через которое освободиться сервер, Kaway - заявки покинувшие систему, Len - длина очереди);

·                   private void button2_Click(object sender, EventArgs e) – функция построения графика, основываясь на полученных ранее значениях.

                  Полученные результаты и их анализ

 

Посредством разработанного программного модуля построим график зависимости необходимого количества серверов от интенсивности потока клиентов.

Моделирование будет происходить при значении математического ожидания случайной величины  (интенсивности) равном значению из диапазона [10, 4000] мс и среднеквадратичном отклонении (дисперсии случайной величины), изменяющимся в диапазоне [10, 500] мс.

Зависимость будем строить по следующей методике:

1)    Изначально зафиксируем математическое ожидание клиентского времени;

2)    При фиксированном математическом ожидании последовательно изменяем значение среднеквадратичного отклонения клиентского времени;

3)    В случае, если очередь поступивших заявок переполняется, добавляем еще один сервер;

4)    Производим перераспределение клиентов и серверов;

5)    Далее фиксируем другое значение математического ожидания и повторяем процесс.

Моделирование, согласно алгоритму, производится с шагом, равным 50 мс, достаточным для достижения необходимой точности при анализе рассматриваемой системы.

Интервал времени для рассмотрения ограничим 2000 мс. Характер зависимости при большей длительности моделирования принимает, условно, установившейся характер и не даёт ценной информации при анализе. В условиях работы максимальное количество серверов, необходимое для работы сети с пренебрежимо малым числом отказов, было принято равным 10, а размер очереди был условно принятой константой размером в 30 заявок. Стоит упомянуть, что в случае, если обработано 10000 заявок, и при этом число заявок, покинувших систему, не превысило 0,01% от общего числа заявок, то моделирование заканчивается.

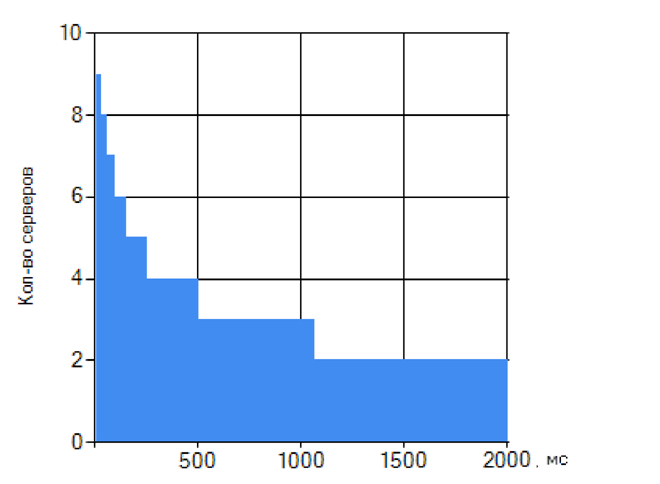
Рис. 5. График зависимости на промежутке от 50 до 2000 мс

 

 

Аппроксимируем полученную зависимость и получим искомый в текущем исследовании график.

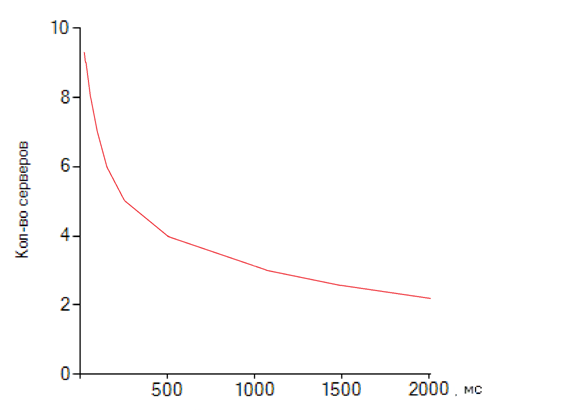
Рис. 6. Аппроксимированный график зависимости необходимого количества серверов

 

Из представленного выше графика видно, что после 1000 мс характер зависимости изменяется, а при рассмотрении той же самой зависимости в более широких пределах (например, до 5000 мс), можно наблюдать, что функция приобретает некоторое, условно, устойчивое значение. Это обусловлено экспоненциальными свойствами потока, реализованного в работе.

Исходя из проведённых выше экспериментов, можно заметить, что при постоянной интенсивности потока клиентов, необходимость использования большего количества серверного оборудования изменяется пропорционально с ростом количества клиентов сети, что совершенно логично и ожидаемо. Причем при небольшом входном потоке клиентов (экспериментально – в среднем до 50 клиентов), можно ограничиться использованием только одного сервера. Далее, при кратном увеличении числа клиентов, потребность в количестве оборудования неизбежно растёт.

Литература

 

1.     В.М. Вишневский Теоретические основы проектирования  компьютерных  сетей. – М.: Техносфера, 2003. – 512 с.

2.     Советов Б. Я., С. А. Яковлев Моделирование систем. – М.: Высш. шк., 1985. – 373 с.

3.     Рихтер Дж. CLR via C#. Программирование на платформе Microsoft .NET Framework 4.5 на языке C#. 4-е изд. – СПб.: Питер, 2013. – 896 с.

4.Албахари Дж., Албахари Б. С# 5.0. Справочник. Полное описание языка.: Пер. с англ.– М.: ООО «И.Д. Вильямс», 2014. – 1008 с.