ПОЛУЧЕНИЕ ПСЕВДОСЛУЧАЙНЫХ СИГНАЛОВ С ТРЕБУЕМЫМ ТИПОМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ

Артюхов О.И., Еремеева В.И.

(Москва, НИУ МЭИ, Россия)

В данной статье рассматривается метод получения псевдослучайных сигналов с требуемым законом распределения, основанный на специальном отображении состояний двоичного регистра сдвига на область действительных чисел.

Несмотря на то, что в НИУ «МЭИ» давно проводятся исследования в данном направлении, не все проблемы успешно решены.

Алгоритм получения псевдослучайных сигналов (ППС) методом отображения заключается в суммировании с некоторым весовыми коэффициентами псевдослучайных двоичных сигналов (ПСДС), снимаемых с разных ячеек регистра сдвига генератора ПСДС, то есть

где (i) – ПСДС, снимаемый с j-ой ячейки генератора, - весовой коэффициент.

С учетом того, что

равенство (1) может быть представлено в виде:

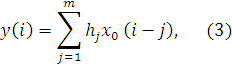
Здесь (i) - ПСДС, подаваемый на вход первой ячейки регистре сдвига.

Процедура синтеза сигнала y(i) с заданным законом распределения сводится к выбору значений весовых коэффициентов .

Известно (2), что существует взаимно-однозначное соответствие между функцией плотности распределения и характеристической функцией , определяемой соотношением:

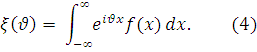
Основные свойства характеристической функции (которые будут использованы в дальнейшем):

· .

· для всех .

Так как , , то получается:

· , то есть и являются комплексно-сопряженными величинами.

· Характеристическая функция действительно тогда и только тогда, когда плотность распределения симметрична. Следовательно

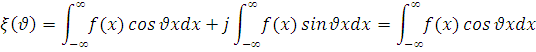
· Сумма m независимых случайных величин с характеристическими функциями .

· Различным плотностям распределения вероятностей соответствуют различные характеристические функции, то есть функция плотности распределения однозначно определяется по своей характеристической функции .

Далее получим выражения для характеристических функций, отвечающих наиболее распространенными типовым законам распределения(2).

1) Равномерное распределение.

Аналитическое выражение для имеет вид

Плотности распределения вероятностей (5) будет соответствовать характеристическая функция.

2) Треугольное распределение (закон Симпсона).

Аналитическое выражение для имеет вид:

Характеристическая функция, соответствующая плотности вероятностей (7), определяется выражением

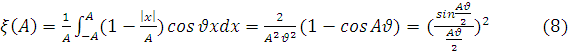
Сравнив выражение (6) и (8) видно, что распределение Симпсона можно рассматривать как композиция двух равномерных распределений на интервале

3) Нормальное распределение.

Аналитическое выражение для плотности распределения вероятностей имеет вид

где - математическое ожидание случайной величины; будем рассматривать случай, когда =0.

- среднеквадратичное отклонение случайной величины ее математического ожидания.

Характеристическая функция, соответствующая нормальному закону распределения, определяется выражением

Из свойств ПСДС известно (1), что плотность распределения вероятностей сигнала, снимаемого с –ой ячейки сдвига генератора ПСДС и взвешенного с весом , имеет вид :

Плотность распределения, определяемой выражением (11), будет соответствовать характеристическая функция вида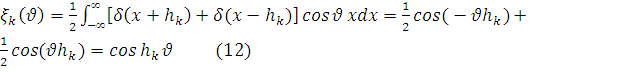

Так как сигналы, снимаемые с ячеек регистра сдвига, практически можно рассматривать статистически независимыми, то характеристическая функция ППС y(i) будет равна произведению характеристических функций сигналов, снимаемых с отдельных ячеек, то есть

Тогда задача получения сигнала с заданной плотностью распределения вероятностей сводится к задаче нахождения весовых коэффициентов, обеспечивающих наилучшую аппроксимацию характеристической функции, соответствующей , выражением (13).

При этом алгоритм расчета весовых коэффициентов определяется видом характеристической функции моделируемого сигнала. Для случайных процессов, характеристическая функция которых имеет периодически повторяющиеся нули, значения весовых коэффициентов находятся из условия совпадения нулей характеристической функции ППС y(i), определяемой выражением (13), с нулями характеристической функции, соответствующей заданному закону распределения, так как значения нулей функции (13) однозначно определяют ее поведение и в остальной области изменения аргумента . Если заданная характеристическая функция является монотонной и не имеет нулей, то коэффициенты ( выбираются одинаковыми, то есть , соблюдая условие равенства площадей, ограниченных характеристическими функциями и , то есть

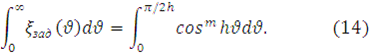
Введем в соотношении (14) обозначения

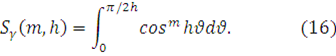
Затем (16) можно представить в виде следующего табличного интеграла(3)

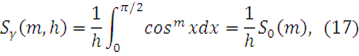
где

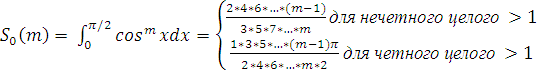(18)

С учетом (15) и (17) получим

Для оценки точности можно использовать критерий вида

который представляет собой величину средней абсолютной ошибки, с которой воспроизводится функция .

Применим описанную методику определения весовых коэффициентов для распределений, рассмотренных выше.

1. Равномерное распределение.

Корни характеристической функции определяются из условия ФФФФ(21)

и равны

Из условия совпадения первых корней характеристических функций (21) и (13) получим, что . Отсюда .

В силу периодичности член вида в разложении (13) будет обращаться в ноль при значениях и так далее, которые совпадают со значениями нечетных корней моделируемой характеристической функции (21). Из условия совпадения вторых корней имеем, что Отсюда .

В силу периодичности чела вида будет иметь корни, совпадающие корнями моделируемой характеристической функции:

Коэффициент получается из условия совпадения четвертых корней функций (21) и (13) (третье корни совпали за счет выбора первого весового коэффициента), то есть Отсюда .

В силу периодичности будет иметь корни, совпадающие со следующими корнями заданной характеристической функции Продолжая указанную процедуру, можно последовательно получить значение всех требуемых коэффициентов

Из изложенного следует, что для получения псевдослучайного сигнала с равномерным законом распределения на интервале весовые коэффициенты определяются по формуле

(22)

2. Треугольное распределение.

Корни характеристической функции определяются из условия

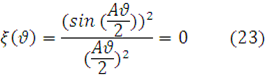
и равны

Из условия совпадения первых корней характеристической функции (23) и (13) , получим, что Отсюда .

В силу периодичности член вида в разложении (13) будет иметь корни, совпадающие с нечетными корнями характеристической функции

Так как при всех значениях характеристическая функция , то ее поведение в окрестности первого корня моделируется членом вида . Следовательно ,

Третий весовой коэффициент находится из условия совпадения вторых корней функций (23) и (13), то есть Отсюда .

В силу периодичности член вида будет иметь корни, совпадающие со следующими корнями характеристической функции (23): и так далее.

По отмеченной выше причине принимается равным .

Следующий весовой коэффициент находится из условия совпадения четверых корней функций (23) и (13), так как совпадение третьи корней указанных функций обеспечено наличием в разложении (13) члена вида . Тогда Отсюда Принимаем .

В силу периодичности член вида будет иметь корни, совпадающие со следующими корнями характеристической функции

Продолжается указанную процедуру, можно последовательно рассчитать все требуемые коэффициенты . Из этого следует, что для получения псевдослучайного сигнала y(i) с треугольным законом распределения плотности вероятностей на интервале весовые коэффициенты следует определять по формуле .

Характеристические функции, соответствующие рассмотренным распределениями, хорошо аппроксимируются выражением (13). Точность аппроксимации зависит от числа скомпенсированных нулей заданной характеристической функции, то есть от числа присутствующих членов разложения (от числа ячеек регистра сдвига).

3. Нормальное распределение

Введя обозначение , получаем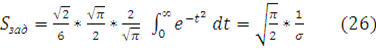

тогда .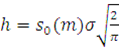

В ходе дальнейшей работы планируется рассмотреть вопрос реализации алгоритма получения псевдослучайных сигналов с заданным законом распределения, основанного на использовании метода отображения состояний двоичного регистра сдвига генератора ПСДС.

Литература

1. Г.С Чхартишвили, В.И. Донеценко. Идентификация динамических объектов управления с применением псевдослучайных сигналов. М.: МЭИ, 1976, -78с.

2. В. Феллер. Введение в теорию вероятностей и ее приложения. М.:1967, том-2, 751с.

3. Горлач, Б. А. Теория вероятностей и математическая статистик. СПб.:2013 . –71с.