BC/NW 2019№ 2 (35):3.1

РАЗРАБОТКА ПРОГРАММЫ КЛАССИФИКАЦИИ НЕСТРУКТУРИРОВАННЫХ ТЕКСТОВЫХ ДОКУМЕНТОВ

Бровкин К. Е.

Задача категоризации (каталогизации, рубрикации) документов, то есть отнесение документа к одной или нескольким темам, является весьма актуальной в связи с ростом объема доступной полнотекстовой информации. Эта задача имеет важные приложения в реальной жизни. Например, новые художественные произведения обычно разделяют по жанрам, а научные статьи часто разделяют по тематике. Еще одно широко распространенное приложение - фильтрация спама, где e-mail сообщения разделяют на две категории: «спам» и «не спам».

Решать задачу катологизации можно с помощью экспертов, которые на основе своего личного опыта будут относить прочитанный документ к наиболее подходящим темам и подтемам. Однако это способ решения очень не эффективен по времени. Также решать задачу категоризации текстов можно автоматически на основе статистических и метрических алгоритмов классификации, используемых в машинном обучении.

1. Постановка  задачи категоризации текстовых документов

Введем некоторые обозначения. Пусть D — множество (коллекция) текстовых документов, W — множество (словарь) всех употребляемых в них слов, C — множество категорий документов, зафиксированное заранее. Каждый документ d ∈ D представляет собой последовательность слов (w1, . . . , wnd ) из словаря W, где nd — длина документа в словах. Одно и то же слово может повторяться в документе много раз.

Задача категоризации — это задача присвоения булева значения каждой паре {d, c} ∈ D × C. Булево значение 1 означает, что документ d относится к категории c, в то время как значение 0 означает обратное. Более формально, задача категоризации — это задача восстановления неизвестной целевой функции Φ : Φ : D × C → {1, 0}.

Сформулируем два естественных предположения, которых обычно придерживаются, решая задачу категоризации.

 1. Все категории — это только символьные метки, и никакого дополнительного смысла их значения не имеют.

2. При решении задачи категоризации нет никаких дополнительных источников данных, кроме текста документа. В частности, нет файлов с метаданными документов (дата публикации, тип документа, и т. д.).

Переход от задачи категоризации к задаче классификации

Задачу категоризации можно рассматривать как задачу многоклассовой классификации, для которой множество классов — это множество категорий C, множество объектов — множество документов D, множество прецедентов — это заранее известное множество пар {d, c}, где d ∈ D, c ∈ C.

Этапы обработки документов

1) Предобработка и индексация документов.

2) Построение и обучение классификатора.

3) Оценка качества классификации

2. Анализ методов машинного обучения и принятых решений для реализации

2.1. Предобработка и индексация документов

Индексация документов – это построение некоторой числовой модели текста, которая переводит текст в удобное для дальнейшей обработки представление.

В данной работе была использована модель «мешка слов» (bag-of-words), которая позволяет представить документ в виде многомерного вектора слов и их весов в документе. Т.е. каждый текстовый файл разбивается на слова (по пробелам) и подсчитывается количество определённого слова, встреченного в каждом документе и, наконец, каждому слову присваивается целочисленный идентификатор. Каждое уникальное слово в словаре будет соответствовать признаку.

Для обучающих и тестовых документов должен применяться один и тот же метод индексации.

В работе для оценки качества разрабатываемых программных средств используется набор данных 20Newsgroups. Набор данных 20Newsgroups представляет собой коллекцию из 18846 документов в новостных группах, разделенных (почти) равномерно на 20 разных групп новостей.  Была первоначально собрана Кеном Лангом. Коллекция 20 групп новостей стала популярным набором данных для экспериментов в текстовых приложениях методов машинного обучения, таких как классификация текста и текстовая кластеризация.

comp.graphics comp.os.ms-windows.misc comp.sys.ibm.pc.hardware comp.sys.mac.hardware comp.windows.x	rec.autos rec.motorcycles rec.sport.baseball rec.sport.hockey	sci.crypt sci.electronics sci.med sci.space
misc.forsale	talk.politics.misc talk.politics.guns talk.politics.mideast	talk.religion.misc alt.atheism soc.religion.christian

Табл 1. Категории набора данных 20Newsgroups

Обучающая коллекция состоит из  11 314 документов.

Тестовая коллекция состоит из 7 532 документов.

Набор данных 20Newsgroups встроен в библиотеку Scikit-learn, использующуюся в данной работе.

2.2. Программная реализация

Библиотека Scikit-learn имеет компонент высокого уровня, который создаёт векторы объектов «CountVectorizer».

In []:

# Извлечение функций из текстового файла
 
from sklearn.feature_extraction.text import CountVectorizer
count_vect = CountVectorizer()
X_train_counts = count_vect.fit_transform(twenty_train.data) 

#изучение слов из словаря док-тов

#и возврат матрицы Документ-Термины [n_samples, n_features], 

#где где n_samples - кол-во документов в обучающей выборке, 

#n_features - кол-во различных слов во всех документах выборки.
X_train_counts.shape #по сути это вывод размера матрицы в out
Out []: (11314, 130107)
 
, где 11314 - кол-во документов в обучающей выборке, 130107- кол-во различных слов во всех документах выборки.
 

2.3. Определение веса признаков

Определение веса признаков документа в данной работе производилось с помощью вычисления функции TF-IDF. Его основная идея состоит в том, чтобы больший вес получали слова с высокой частотой в пределах конкретного документа и с низкой частотой употреблений в других документах.

Вычисляется частота термина TF (term frequency) - оценка важности слова в пределах одного документа d по формуле

TF = nt,d / nd,

,где nt, d – количество употреблений слова t в документе d; nd - общее число слов в документе d.

Обратная частота документа IDF (inverse document frequency) – инверсия частоты, с которой слово встречается в документах коллекции. IDF уменьшает вес наиболее распространённых слов по формуле

IDF = log( |D| / Dt),

,где |D| – общее количество документов в коллекции; Dt  – количество всех документов, в которых встречается слово t.

Итоговый вес термина в документе относительно всей коллекции документов вычисляется по формуле

Vt, d = TF × IDF.

Следует отметить, что по этой формуле оценивается значимость термина только с точки зрения частоты вхождения в документ, без учета порядка следования терминов в документе и их лексической сочетаемости.

2.4. Программная реализация

In []:

# TF-IDF

from sklearn.feature_extraction.text import TfidfTransformer

tfidf_transformer = TfidfTransformer()

X_train_tfidf = tfidf_transformer.fit_transform(X_train_counts)

X_train_tfidf.shape

Out []: (11314, 130107)
 
, где 11314 - кол-во документов в обучающей выборке, 130107- кол-во различных слов во всех документах выборки.
 

3. Классификация методом Байеса

3.1. Расчетные соотношения метода Байеса

Метод Байеса (Naive Bayes, NB) относится к вероятностным методам классификации.

Пусть P(ci|d) – вероятность того, что документ, представленный вектором d = (t1, …, tn), соответствует категории ci для i = 1, …, |C|. Задача классификатора заключается в том, чтобы подобрать такие значения ci и d, при которых значение вероятности P(ci|d) будет максимальным:

Для вычисления значений P(ci|d) пользуются теоремой Байеса:

,  

где P(ci) – априорная вероятность того, что документ отнесен к категории ci; P(d | ci) – вероятность найти документ, представленный вектором d = (t1, …, tn), в категории ci; P(d) – вероятность того, что произвольно взятый документ можно представить в виде вектора признаков d = (t1, …, tn).

По сути P(ci) является отношением количества документов из обучающей выборки L, отнесенных в категорию ci , к количеству всех документов из L.

P(d) не зависит от категории ci, а значения t1, …, tn заданы заранее, поэтому знаменатель – это константа, не влияющая на выбор наибольшего из значений P(ci|d).

Вычисление P(d | ci) затруднительно из-за большого количества признаков t1, …, tn , поэтому делают «наивное» предположение о том, что любые две координаты, рассматриваемые как случайные величины, статистически не зависят друг от друга. Тогда можно воспользоваться формулой

.

Далее все вероятности подсчитываются по методу максимального правдоподобия.

3.2. Программная реализация классификации методом Байеса

Категоризация тестовой выборки текстовых документов классификатором обученным на обучающей выборке

In []:

# Machine Learning

# Training Naive Bayes (NB) classifier on training data.

from sklearn.naive_bayes import MultinomialNB

from sklearn.pipeline import Pipeline

text_clf = Pipeline([('vect', CountVectorizer()), ('tfidf', TfidfTransformer()), ('clf', MultinomialNB())])

text_clf = text_clf.fit(twenty_train.data, twenty_train.target)

# Performance of NB Classifier

import numpy as np

#numpy - библиотека питона для работы с массивами

import timeit

#timeit - библиотека питона для измерения времени

start_time = timeit.default_timer()

twenty_test = fetch_20newsgroups(subset='test', shuffle=True)

predicted = text_clf.predict(twenty_test.data)

#text_clf.predict - Применить преобразования к данным и предсказать с помощью окончательной оценки

viv = np.mean(predicted == twenty_test.target)

#np.mean - вычисляет точность метода

elapsed = timeit.default_timer() - start_time

print (elapsed, viv)

Точность метода: 0.7738980350504514 
Время выполнения: 2.90606 сек.

4. Классификация методом опорных векторов

4.1. Расчетные соотношения метода опорных векторов

Метод опорных векторов (Support Vector Machine, SVM) является линейным методом классификации.

Рассмотрим множество документов, которые необходимо расклассифицировать. Сопоставим ему множество точек в пространстве размерности |D|.

Выборку точек называют линейно разделимой, если принадлежащие разным классам точки можно разделить с помощью гиперплоскости (в двухмерном случае гиперплоскостью является прямая линия). Очевидный способ решения задачи в таком случае - провести прямую так, чтобы по одну сторону от нее лежали все точки одного класса, а по другую - все точки другого класса. Тогда для классификации неизвестных точек достаточно будет посмотреть, с какой стороны прямой они окажутся.

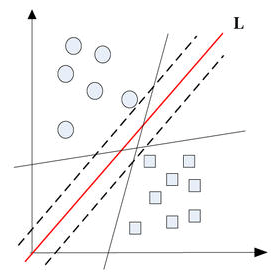
В общем случае можно провести бесконечное множество гиперплоскостей (прямых), удовлетворяющих условию. Ясно, что лучше всего выбрать прямую, максимально удаленную от имеющихся точек. В методе опорных векторов расстоянием между прямой и множеством точек считается расстояние между прямой и ближайшей к ней точкой из множества. Именно такое расстояние и максимизируется в данном методе. Гиперплоскость, максимизирующая расстояние до двух параллельных гиперплоскостей, называется разделяющей (на рисунке 1 обозначена буквой L). Ближайшие к параллельным гиперплоскостям точки называются опорными векторами (рис. 1), через них проходят пунктирные линии. Другими словами, алгоритм работает в предположении, что, чем больше разница или расстояние между этими параллельными гиперплоскостями, тем меньше будет средняя ошибка классификатора, так как максимизация зазора между классами способствует более уверенной классификации.

4.2 Программная реализация метода опорных векторов

# Support Vector Machines Classifier

from sklearn.linear_model import SGDClassifier

text_clf_svm = Pipeline([('vect', CountVectorizer()), ('tfidf', TfidfTransformer()),

                         ('clf-svm', SGDClassifier(loss='modified_huber', penalty='l2',alpha=1e-4, max_iter=7, random_state=2))])

start_time = timeit.default_timer()

text_clf_svm = text_clf_svm.fit(twenty_train.data, twenty_train.target)

predicted_svm = text_clf_svm.predict(twenty_test.data)

viv = np.mean(predicted_svm == twenty_test.target)

elapsed = timeit.default_timer() - start_time

print (elapsed, viv)

Точность метода: 0.82381837493361654
Время выполнения: 7.88170 сек.

5. Повышение эффективности методов подбором параметров

Почти все классификаторы будут иметь различные параметры, которые могут быть настроены для получения оптимальной точности.  Библиотека Scikit имеет чрезвычайно полезный инструмент «GridSearchCV», который позволяет задать список параметров, для которых мы хотели бы выполнить настройку точности и настраивает классификатор автоматически, подбирая оптимальные параметры. 

5.1. Классификация методом Байеса

# Grid Search

from sklearn.model_selection import GridSearchCV

parameters = {'vect__ngram_range': [(1, 1), (1, 2)], 'tfidf__use_idf': (True, False), 'clf__alpha': (1e-2, 1e-3)}

gs_clf = GridSearchCV(text_clf, parameters, n_jobs=-1)

gs_clf = gs_clf.fit(twenty_train.data, twenty_train.target

gs_clf.best_score_

gs_clf.best_estimator_

Параметры необходимые для получения оптимальной точности классификатора:
 
Pipeline(memory=None,
     steps=[('vect', CountVectorizer(analyzer='word', binary=False, decode_error='strict',
        dtype=<class 'numpy.int64'>, encoding='utf-8', input='content',
        lowercase=True, max_df=1.0, max_features=None, min_df=1,
        ngram_range=(1, 2), preprocessor=None, stop_words=None,
        strip...near_tf=False, use_idf=True)), ('clf', MultinomialNB(alpha=0.01, class_prior=None, fit_prior=True))])
 
 
Точность метода с учётом найденных параметров: 0.90675269577514583
 

5.2. Классификация методом опорных векторов

# Grid Search

from sklearn.model_selection import GridSearchCV

parameters_svm = {'vect__ngram_range': [(1, 1), (1, 2)], 'tfidf__use_idf': (True,False), 'clf-svm__loss': ('modified_huber', 'squared_hinge', 'hinge'), 'clf-svm__max_iter': (6, 7, 8)}

gs_clf_svm = GridSearchCV(text_clf_svm, parameters_svm, n_jobs=-1)

gs_clf_svm = gs_clf_svm.fit(twenty_train.data, twenty_train.target)

gs_clf_svm.best_params_

gs_clf.best_estimator_

Параметры необходимые для получения оптимальной точности классификатора:
 
Pipeline(memory=None,
     steps=[('vect', CountVectorizer(analyzer='word', binary=False, decode_error='strict',
        dtype=<class 'numpy.int64'>, encoding='utf-8', input='content',
        lowercase=True, max_df=1.0, max_features=None, min_df=1,
        ngram_range=(1, 2), preprocessor=None, stop_words=None,
        strip...lty='l2', power_t=0.5, random_state=2,
       shuffle=True, tol=None, verbose=0, warm_start=False))])

Точность метода с учётом найденных параметров: 0.92266218843910197

5.3. Пример влияния изменения параметров классификатора на точность для метода опорных векторов

Параметры по умолчанию:

text_clf_svm = Pipeline([('vect', CountVectorizer()), ('tfidf', TfidfTransformer()),

('clf-svm', SGDClassifier(loss='hinge', penalty='l2',alpha=1e-3, max_iter=5, random_state=42))])

Точность: 0.82381837493361654

max_iter - Максимальное количество итераций

Изменение параметра max_iter=10:

text_clf_svm = Pipeline([('vect', CountVectorizer()), ('tfidf', TfidfTransformer()),

('clf-svm', SGDClassifier(loss='hinge', penalty='l2',alpha=1e-3, max_iter=10, random_state=42))])

Точность: 0.82421667551779076, точность на ~0.0004 выше, чем с параметрами по умолчанию 

Изменение параметра max_iter=100:

text_clf_svm = Pipeline([('vect', CountVectorizer()), ('tfidf', TfidfTransformer()),

('clf-svm', SGDClassifier(loss='hinge', penalty='l2',alpha=1e-3, max_iter=100, random_state=42))])

Точность: 0.82408390865639936, точность на ~0.0002 выше, чем с параметрами по умолчанию.

alpha  - константа, которая умножается на член регуляризации.

Изменение параметра alpha=1e-2:

text_clf_svm = Pipeline([('vect', CountVectorizer()), ('tfidf', TfidfTransformer()),

('clf-svm', SGDClassifier(loss='hinge', penalty='l2',alpha=1e-2, max_iter=5, random_state=42))])

Точность: 0.82209240573552844, точность на ~ 0.0018 ниже, чем с параметрами по умолчанию.
 

Изменение параметра alpha=1e-4:

text_clf_svm = Pipeline([('vect', CountVectorizer()), ('tfidf', TfidfTransformer()),

('clf-svm', SGDClassifier(loss='hinge', penalty='l2',alpha=1e-4, max_iter=5, random_state=42))])

Точность: 0.85103558151885295, точность на ~0.0272 выше, чем с параметрами по умолчанию.
 
Изменение параметра alpha=1e-5:

text_clf_svm = Pipeline([('vect', CountVectorizer()), ('tfidf', TfidfTransformer()),

('clf-svm', SGDClassifier(loss='hinge', penalty='l2',alpha=1e-5, max_iter=5, random_state=42))])

Точность: 0.83736059479553904, точность на ~0.0135 выше, чем с параметрами по умолчанию.
 

Изменение параметра alpha=1e-6:

text_clf_svm = Pipeline([('vect', CountVectorizer()), ('tfidf', TfidfTransformer()),

('clf-svm', SGDClassifier(loss='hinge', penalty='l2',alpha=1e-6, max_iter=5, random_state=42))])

Точность: 0.81956983536909189, точность на ~0.0042 ниже, чем с параметрами по умолчанию.
 

6. Сравнение точности и времени выполнения построенных классификаторов

	Метод Байеса с параметрами по умолчанию	Метод Байеса с оптимально подобранными параметрами	Метод опорных векторов с параметрами по умолчанию	Метод опорных векторов с оптимально подобранными параметрами
Точность, %	77,38980	90,67526	85,44875	92,26621
Время, сек	2,90606	6,21861	7,88170	21,81160

Заключение

В данной работе была решена задача категоризации текстовых документов на наборе данных 20Newsgroups. Были разобраны все этапы обработки документов, такие как индексация документов, построение и обучение классификатора с помощью двух методов, произведена оценка качества классификации.

Коллекция текстовых документов была проиндексирована методом «мешка слов» (bag-of-words)  и определён вес признаков документа функцией TF-IDF.

Были построены и обучены два классификатора: методом Байеса и методом опорных векторов. Также точность классификаторов была улучшена подбором оптимальных параметров.

В ходе сравнения построенных  классификаторов можно сделать вывод: метод Байеса по сравнению с методом опорных векторов показывает наилучшее время выполнения, но худшую точность. Также подбор оптимальных параметров улучшает точность методов, но повышает время выполнения.

Литература

1. Батура Т.В. Методы автоматической классификации текстов // Программные продукты и системы. – 2017. – № 1. – С. 85-99

2. Sebastiani, Fabrizio Machine learning in automated text categorization // ACM Computing Surveys, 2002, vol. 34, pp. 1-47.

3. [Электронный ресурс]. URL: http://scikit-learn.org

4. [Электронный ресурс]. URL: http://www.machinelearning.ru/wiki/index.php

5. [Электронный ресурс]. The 20 Newsgroups data set URL: http://qwone.com/~jason/20Newsgroups/

6. [Электронный ресурс]. URL: http://www.scholarpedia.org/article/Text_categorization

7. [Электронный ресурс]. URL: https://habrahabr.ru/post/319288/