BC/NW 2019№ 2 (35):6.1
СРАВНЕНИЕ МЕТОДОВ КЛАСТЕРНОГО АНАЛИЗА НА ЭЛЕМЕНТАРНОМ НАБОРЕ ДАННЫХ
Школьникова Д.Д.
Главная задача кластерного анализа – выделить необходимое число групп (кластеров) среди заданных объектов так, чтобы объекты внутри групп были максимально схожи, а сами группы максимально отличны друг от друга. В отличии от классификации, для кластерного анализа не требуется предположений об исследуемом наборе данных, кроме того, что данные должны быть представлены в сравнимых шкалах.
Критерий определения схожести и различия кластеров – это расстояние между точками на диаграмме рассеивания. Способов определения меры расстояния между кластерами, называемой еще мерой близости, существует несколько. Наиболее распространенный способ - вычисление евклидова расстояния между двумя точками i и j на плоскости, когда известны их координаты X и Y:
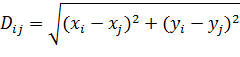
В среднем, вне зависимости от вида алгоритма кластерного анализа, для каждого из них можно выделить несколько этапов:
1. Выбор объектов кластеризации.
2. Определение критериев, по которым будет проводиться группирование.
2.1. Если данные не нормализованы, то – нормализация их значений.
3. Определение меры сходства между значениями.
4. Применение алгоритма кластеризации для группирования объектов.
5. Получение результатов.
Существует ряд сложностей, которые следует продумать перед проведением кластеризации:
· ∙Сложность выбора характеристик, на основе которых проводится кластеризация. Необдуманный выбор приводит к неадекватному разбиению на кластеры и, как следствие, - к неверному решению задачи.
· ∙Сложность выбора метода кластеризации. Этот выбор требует неплохого знания методов и предпосылок их использования. Чтобы проверить эффективность конкретного метода в определенной предметной области, целесообразно применить следующую процедуру: рассматривают несколько априори различных между собой групп и перемешивают их представителей между собой случайным образом. Далее проводится кластеризация для восстановления исходного разбиения на кластеры. Доля совпадений объектов в выявленных и исходных группах является показателем эффективности работы метода.
· ∙Проблема выбора числа кластеров. Если нет никаких сведений относительно возможного числа кластеров, необходимо провести ряд экспериментов и, в результате перебора различного числа кластеров, выбрать оптимальное их число.
· ∙Проблема интерпретации результатов кластеризации. Форма кластеров в большинстве случаев определяется выбором метода объединения. Однако следует учитывать, что конкретные методы стремятся создавать кластеры определенных форм, даже если в исследуемом наборе данных кластеров на самом деле нет.
2 Программная реализация алгоритмов.
На данный момент не существует общепринятой классификации способов кластеризации, но можно выделить некоторые группы подходов:
· Строящиеся «снизу-вверх» и «сверху-вниз»
· Монотетические и политетические
· Непересекающиеся и нечеткие
· Детерменированные и стохастические
· Потоковые (online) и не потоковые
· Зависящие и независящие от начального разбиения
· Зависящие и независящие от порядка разбиения объектов
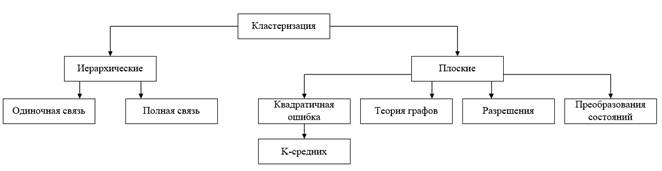
Рис.1. Дерево классификации алгоритмов кластеризации.
В выполняемой работе рассмотрены несколько наиболее ярких методов кластеризации, такие, как:
Этот алгоритм является алгоритмом нечеткой кластеризации. Такое алгоритмы основаны на предположении, что каждый элемент принадлежит каждому кластеру в определенной степени. Такие алгоритмы будут крайне полезны при решении задачи разбиения объектов на близко находящиеся друг к другу кластеры. Однако, для выполнения этого алгоритма требуется большой объем вычислительных ресурсов, а также задание количества кластеров. Также слабым местом этого типа алгоритмов является то, что может возникнуть неоднозначность в разбиении объектов, равноудаленных от центров кластеров.
2.1 Алгоритм метода:
1. Распределить точки по кластерам случайным образом.
2. Для каждого кластера найти его центр, для этого считаем покомпонентное среднее всех относящихся к нему точек, причем каждая точка берется с весом, равным степени ее принадлежности к кластеру:
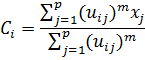
Где p – число объектов разбиения, m – коэффициент нечеткости разбиения, u – степень принадлежности каждому кластеру, x – объект.
3. Пересчитываем матрицу распределения по следующей формуле:
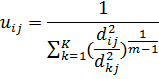
4. Если на предыдущем шаге матрица распределения изменилась меньше, чем на заданное значение критерия окончания, прекращаем работу. Иначе переходим к пункту 2.
5. Результат работы алгоритма - текущее разбиение точек на кластеры.
Для того, чтобы сравнение при тестировании было корректным, примем гипотезу, что объект принадлежит кластеру, если степень распределения данного объекта к данному кластеру выше, чем к другим кластерам.
FOREL (Формальный Элемент) - алгоритм кластеризации, основанный на идее объединения в один кластер объектов в областях их наибольшего сгущения.
Цель данного метода – разбиение объектов на такое число кластеров, чтобы сумма расстояний объектов до центров кластеров, которым они принадлежат, была минимальной для каждого кластера. То есть, необходимо сформировать группы максимально близких друг к другу объектов.
Одними из главных преимуществ данного алгоритма считаются его наглядность и сходимость. Однако, данный алгоритм плохо применим при плохой разделимости выборки на кластеры.
2.2 Алгоритма FOREL
В работе алгоритма FOREL можно выделить следующие шаги:
1. Случайный выбор текущего объекта выборки. На данном этапе считаем его центром кластера.
2. Выделение объектов выборки, находящихся на расстоянии менее, чем задаваемое значение R от текущего центра.
3. Вычисление центра тяжести. Считаем, что выделенный центр тяжести будет также центром данного кластера и новым текущим объектом выборки.
4. Повторение шагов 2-3, пока новый текущий объект не совпадет с прежним
5. Считаем, что объекты внутри сферы заданного радиуса R вокруг текущего объекта кластеризованные. Больше не рассматриваем их в выборке.
6. Повторение шагов 1-5, пока не будет кластеризована вся выборка
Основываясь на достоинствах и недостатках вышеперечисленных алгоритмов, а также на общем представлении об алгоритмах кластеризации, выделим основные критерии сравнения алгоритмов:
1. Простота реализации.
2. Чувствительность к выбросам.
3. Зависимость от входных данных.
Проверка работы алгоритма С-средних (малое количество заранее известных значений).
Исходные данные:
Число точек – 4.
Число групп – 2.
Заданные точки: (10;20), (20,10), (100;100), (110;110).
Ожидаемый результат: Точки (10;20) и (20,10) объединятся в первый кластер, а (100;100) и (110;110) во второй.
Результат:

Рис.2. Проверка работы алгоритма C-средних (малое количество заранее известных значений).
Как видно на изображении, точки распределились ожидаемым образом – первый кластер отмечен белым цветом, а второй – голубым.
Можем сделать вывод, что на малом количестве заранее известных значений алгоритм работает корректно.
Проверка работы FOREL (малое количество заранее известных значений).
Исходные данные:
Число точек – 4.
Радиус кластера – 50.0.
Заданные точки: (10;20), (20,10), (100;100), (110;110).
Ожидаемый результат: Точки (10;20) и (20,10) объединятся в первый кластер, а (100;100) и (110;110) во второй.
Результат:

Рис.3. Проверка работы алгоритма FOREL (малое количество заранее известных значений).
Как видно на изображении, точки распределились ожидаемым образом – первый кластер отмечен голубым цветом, а второй – белым.
Можем сделать вывод, что на малом количестве заранее известных значений алгоритм работает корректно.
Проверка работы алгоритма C-средних (большое количество объектов в определенном диапазоне).
Исходные данные:
Число точек – 200.
Число групп – 2.
Точки заданы на диапазонах (0;0) - (100,120) и (500;150) - (720,400).
Ожидаемый результат: Точки на первом и втором диапазонах объединятся в соответствующую пару кластеров.
Результат:

Рис.4. Проверка работы алгоритма C-средних (большое количество объектов в определенном диапазоне).
Как видно на изображении, точки распределились ожидаемым образом – кластеры отмечены белым и голубым цветами.
Можем сделать вывод, что алгоритм будет работать также и на большом количестве объектов.
Проверка работы алгоритма FOREL (большое количество объектов в определенном диапазоне).
Исходные данные:
Число точек – 200.
Радиус кластера – 200.0.
Точки заданы на диапазонах (0;0) - (100,120) и (500;150) - (720,400).
Ожидаемый результат: Точки на первом и втором диапазонах объединятся в соответствующую пару кластеров.
Результат:

Рис.5. Проверка работы алгоритма FOREL (большое количество объектов в определенном диапазоне).
Как видно на изображении, точки распределились ожидаемым образом – кластеры отмечены белым и голубым цветами.
Можем сделать вывод, что алгоритм будет работать также и на большом количестве объектов.
Исходные данные:
Число точек – 200.
Число групп – 2.
Точки заданы на диапазонах (0;0) - (250,100) и (300;150) - (720,400).
Ожидаемый результат: Точки на первом и втором диапазонах объединятся в соответствующую пару кластеров.
Результат:

Рис.6. Проверка работы алгоритма С-средних (большое количество объектов в определенном диапазоне, группы расположены недалеко друг от друга).
Из-за случайного определения центроидов и близкого расположения групп относительно друг друга, часть объектов розовой группы определилась, как объекты зеленой группы.
Проверка работы алгоритма FOREL (большое количество объектов в определенном диапазоне, группы расположены недалеко друг от друга).
Исходные данные:
Число точек – 200.
Радиус кластера – 200.0.
Точки заданы на диапазонах (0;0) - (250,100) и (300;150) - (720,400).
Ожидаемый результат: Точки на первом и втором диапазонах объединятся в соответствующую пару кластеров.
Результат:

Рис.7. Проверка работы FOREL (большое количество объектов в определенном диапазоне, группы расположены недалеко друг от друга).
Радиус кластера оказался меньше второй группы, поэтому выборка была разделена на 4 кластера. Можно сделать вывод, что данный метод уязвим из-за необходимости задавания величины радиуса.
Проверка работы алгоритма C-средних в случае выброса.
Исходные данные:
Число точек – 200.
Число групп – 2.
Точки заданы на диапазонах (0;0) - (100,120) и (500;150) - (720,400). Также задана точка выброса – (370;330)
Ожидаемый результат: Точки на первом и втором диапазонах объединятся в соответствующую пару кластеров. Точка выброса будет отнесена к ближайшему кластеру.
Результат:

Рис.8. Проверка работы алгоритма С-средних в случае выброса.
Алгоритм корректно отнес точку выброса к голубой группе.
Проверка работы алгоритма FOREL в случае выброса.
Исходные данные:
Число точек – 200.
Радиус кластера – 250.0.
Точки заданы на диапазонах (0;0) - (100,120) и (500;150) - (720,400). Также задана точка выброса – (370;330)
Ожидаемый результат: Точки на первом и втором диапазонах объединятся в соответствующую пару кластеров. Точка выброса будет отнесена к ближайшему кластеру.
Результат:

Рис.9. Проверка работы алгоритма ближайшего соседа в случае выброса.
На изображении можем увидеть, что точка выброса правильно определена к синей группе.
Проверка работы алгоритма С-средних на хаотично расположенных объектах.
Исходные данные:
Число точек – 200.
Число групп – 2.
Точки заданы на диапазоне (0;0) - (720,400).
Ожидаемый результат: Точки разделятся на две группы.
Результат:

Рис.10. Проверка работы алгоритма C-средних на хаотично расположенных объектах.
Объекты разделились на две примерно равные группы с максимально удаленными центрами масс.
Проверка работы алгоритма FOREL на хаотично расположенных объектах.
Исходные данные:
Число точек – 200.
Радиус кластера – 250.0.
Точки заданы на диапазоне (0;0) - (720,400).
Ожидаемый результат: Точки разделятся на неопределенное количество групп в зависимости от их расположения на поле.
Результат:

Рис.11. Проверка работы алгоритма FOREL на хаотично расположенных объектах.
Точки разделились на три кластера – синий кластер с заданным радиусом 250 расположился в центре, еще два кластера находятся справа и слева от него.
Нечеткое распределение алгоритма C-средних
Исходные данные:
Число точек – 200.
Число групп – 3.
Точки заданы на диапазоне (0;0) - (720,400).
Ожидаемый результат: Каждому кластеру присваивается свой цвет (красный, зеленый, синий). Формируется матрица распределения. Каждый элемент будет иметь цвета всех групп в той доле, в которой они принадлежат этим группам.
Результат:

Рис.12. Нечеткое распределение алгоритма C-средних.
Как видно на изображении, все точки были в той или иной степени отнесены к каждому из трех кластеров. Те точки, которые оказались ближе к центрам кластеров, окрашены зеленым, синим или красным цветом. Точки, находящиеся на границах кластеров окрашены сочетаниями этих цветов (например, точки на границе синего и красного кластера имеют фиолетовый цвет).
С помощью различных методов кластерного анализа можно получить разные результаты при одинаковых вводных данных. Это связано с индивидуальными особенностями каждого метода.
Так мы можем увидеть, что алгоритм С-средних может показать неверный результат из-за близкого расположения кластеров. Также недостатком этого алгоритма является то, что необходимо изначально иметь гипотезу о количестве кластеров, что не всегда возможно при исследованиях.
Алгоритм FOREL в этом плане лучше, так как самостоятельно определяет количество кластеров, однако также чувствителен из-за изначально задаваемого радиуса кластера. Следовательно, в случае, если один кластер будет значительно больше другого или при неправильном подборе радиуса алгоритм будет искажать результаты. Однако, другим очевидным преимуществом этого алгоритма является простота понимания его работы и реализации.
Оба рассмотренных алгоритма оказались устойчивы к выбросам, что означает, что единичные отклонения в выборке не будут влиять на общий результат группирования.
Следует также отметить, что алгоритм С-средних может предоставить результат в виде нечеткого распределения объектов по группам, что невозможно реализовать с помощью алгоритма FOREL.
Таким образом, следует помнить, что выбор метода анализа данных будет оказывать существенное влияние на полученные результаты.
1. B.A. Бритвихин, Ф.А. Красина, С.Н. Симонцев Использование кластерного анализа для типологизации признаков, 1994г
2. НОУ «ИНТУИТ» [Электронный ресурс] : https://www.intuit.ru (дата обращения: 21.04.2018)
3. Купалова Г.І. Теорія економічного аналізу: навч. посіб. - К.: Знання, 2008. - 639 с.
4. Близоруков М. Г. Б40 Статистические методы анализа рынка: Учебно-метод. пособие / Близоруков М. Г. – Екатеринбург: Ин-т управления и предпринимательства Урал. гос. ун-та, 2008. – 75 с.
5. Факторный, дискриминантный и кластерный анализ: Пер. с англ./Дж.-О. Ким, Ч. У. Мьюллер, У. Р. Клекка и др.; Под ред. И. С. Енюкова. — М.: Финансы и статистика, 1989.— 215 с.