BC/NW 2019№ 2 (35):7.1

СОГЛАСОВАНИЕ ПРОИЗВОДИТЕЛЬНОСТИ ВЫЧИСЛИТЕЛЬНОГО КЛАСТЕРА С ПРОПУСКНОЙ СПОСОБНОСТЬЮ ДИСКОВОГО МАССИВА ПРИ ОБРАБОТКЕ БОЛЬШИХ ФАЙЛОВ

Рыбинцев В.О.

Рассматривается проблема снижения  производительности вычислительного кластера при обработке больших файлов.  Отмечено, что при заданной пропускной способности дискового массива с ростом числа ядер в кластере время решения задачи сначала падает, а потом, начиная с некоторого значения, начинает расти. Такое поведение системы объясняется тем, что весь выигрыш в производительности нивелируется увеличением времени ожидания в системе хранения, которое растет нелинейно с ростом нагрузки, как во всякой системе с очередью. В качестве дисковых массивов рассматриваются параллельные системы хранения, позволяющие линейно наращивать их пропускную способность. На основе математической модели в виде замкнутой сети массового обслуживания  предлагается приближенный подход к вычислению значения границы, до которой целесообразно увеличивать количество процессорных ядер в вычислительном кластере при заданной пропускной способности дискового массива. Рассмотрены случаи различного соотношения пропускной способности дискового массива и локальной сети. Вводится понятие удельной трудоемкости прикладной задачи, определяющее количество вычислительных операций с плавающей точкой, приходящееся на один байт ввода-вывода данных. С помощью данного понятия получено простое соотношение для приближенного расчета значения искомой границы, использующее в качестве исходных данных результаты стандартных тестов производительности LINPACK и SPC-2. Приведены примеры расчета целесообразного числа ядер в вычислительном кластере и результаты сравнения расчетного значения с результатами натурных измерений, которые показали адекватность предложенного подхода.

1. Введение

Современные суперкомпьютеры, входящие в TOP500 (www.top500.org), ранжируются по производительности в соответствии с результатами теста LINPACK, представляющим собой решение системы линейных уравнений большой размерности. При этом значение производительности измеряется в Flops (Floating Operations per Second). Такой подход вполне обоснован в тех случаях, когда при решении прикладной задачи затраты времени на организацию ввода-вывода данных существенно меньше общего времени счета (тест LINPACK является именно такой задачей). Поэтому задержками на операции ввода-вывода можно пренебречь.

Однако существует класс задач, относящихся к категории High Performance Computing (HPC), в процессе решения которых вычислительный кластер манипулирует огромным объемом информации. При этом затраты времени на организацию ввода-вывода данных становятся существенными, а пропускная способность дискового массива, на котором размещается исходная информация и куда выгружаются результаты расчетов, оказывает существенное влияние на итоговую производительность комплекса.

Примерами таких задач может служить обработка метеорологических данных [1] или данных сейсморазведки [2] с целью построения геологической модели толщи земли в процессе поиска, разведки и разработки залежей углеводородов. Затраты времени на подобные расчеты измеряются многими часами непрерывного счета. Традиционным путем сокращения времени счета является наращивание количества процессорных ядер в кластере с последующим комплексом мероприятий по повышению пропускной способности системы хранения.

Вопросу повышения пропускной способности систем хранения при заданном количестве процессорных ядер посвящено большое количество работ, в которых предлагаются различные подходы к снижению задержек в системах хранения. С этой целью   используют  SSD диски с особыми алгоритмами управления буферизацией [3], распределенные файловые системы [4 - 7],  специальные алгоритмы планирования рабочей нагрузки [8] и сегментирования данных [9, 10],  применяют архитектуру MPP (Massive Parallel Processing) для организации хранения данных [11], а также повышают пропускную способность среды подключения дисковых массивов [12].

В отличие от указанных работ, в настоящей статье производительность вычислительного комплекса, относящегося к категории HPC и ориентированного на обработку больших файлов, исследуется со стороны вычислительного кластера. Отметим, что необходимость оперировать терабайтными объемами данных в процессе вычислений приводит к следующему неожиданному эффекту: с ростом количества процессорных ядер в кластере общее время счета сначала снижается, но по достижении некоторого количества ядер не только перестает уменьшаться, но даже начинает расти. Данную зависимость времени решения прикладной задачи от количества процессорных ядер можно увидеть в [13] и  [14].

Указанный эффект объясняется тем, что с ростом числа процессорных ядер повышается нагрузка на подсистему ввода-вывода, задержка в которой, как и во всякой системе массового обслуживания, растет нелинейно с ростом нагрузки. Это приводит к тому, что весь выигрыш от потенциального роста производительности кластера за счет большего уровня параллелизма нивелируется возрастающим временем ожидания в системе хранения данных.

Поэтому, задача определения верхней границы числа процессорных ядер в кластере, до которого это количество целесообразно наращивать при заданной пропускной способности дискового массива, представляется   актуальной.

При определении указанной границы необходимо учитывать, что для повышения пропускной способности дискового массива   традиционно используют параллельные файловые системы и параллельные системы хранения, к которым относятся, например, ISILON [15] или PANASAS [16] в различных модификациях. Основная идея построения таких массивов заключается том, что они имеют модульную конструкцию,    каждый модуль которой представляет собой автономную систему хранения, работающую параллельно с другими под управлением параллельной файловой системы. При этом для приложений, использующих такой массив, он представляется единой системой хранения.   Добавление новых модулей приводит к пропорциональному росту пропускной способности  массива, которая может достигать 200 Гбайт/с [15].

Еще одной особенностью, которую необходимо учитывать при решении обозначенной задачи, является пропускная способность локальной сети, через которую осуществляется взаимодействие кластера с системой хранения.

В данной работе сначала будет рассмотрен случай использования   традиционного файлового сервера или дискового массива NAS (Network Attach Storage), работающего по протоколу NFS, затем случай применения параллельной системы хранения, и наконец, учтено влияние пропускной способности локальной сети на искомую границу числа процессорных ядер.

Для учета некоторых специфических особенностей решаемой задачи, сформулируем два важных замечания.

Замечание 1. Точность определения искомой границы числа процессорных ядер может быть достаточно низкой, так как наиболее распространенные современные процессоры (Intel Xeon) содержат более 20-ти ядер, а узлы кластера представляют собой, как правило, двухпроцессорные серверы. Поэтому, изменение количества процессорных ядер в кластере происходит дискретно с шагом прядка 50. Следовательно, определение искомой границы с большей точностью не имеет смысла.

Замечание 2. Итоговое  соотношение должно быть простым и не требовать существенных усилий для получения исходных данных для расчета. В противном случае, такое соотношение не будет практически значимым.

2. Методы исследования

2.1. Математическая модель комплекса с традиционной  системой хранения

Для исследования задержек, возникающих в процессе обработки, передачи и хранения данных в вычислительных системах различного класса, включая HPC, традиционно используется аппарат теории очередей [17, 18].

Рассмотрим процесс функционирования комплекса обработки больших файлов. Основными элементами комплекса являются вычислительный кластер, дисковый массив класса NAS (Network Attach Storage) или файловый сервер, работающие по протоколу NFS, и локальная сеть. В упрощенном виде процесс обработки данных заключается в следующем:  после процедуры начальной инициализации (INIT) каждый узел кластера считывает некоторый объем данных (RD) с дискового массива, осуществляет его обработку (CALC) и записывает результат на дисковый массив (WR). Данный процесс повторяется многие сотни и даже тысячи раз, пока весь объем данных не будет обработан. Рис. 1 иллюстрирует данный процесс.

Рис. 1. Временная диаграмма обработки большого файла  

На Рис. 1 умышленно не показаны затраты времени на передачу данных по локальной сети между массивом и узлами кластера. Современные сети в рассматриваемых системах используют, как правило, технологию Infiniband QDR или FDR с пропускной способностью 40 Гбит/c или 56 Гбит/с соответственно. Это существенно превосходит пропускную способность системы хранения, и, потому, учитывая замечание 1, данными задержками можно пренебречь (позже мы вернемся к этому вопросу и рассмотрим случай, когда данное условие не выполняется). Тогда в качестве   модели процесса обработки большого файла можно использовать  замкнутую систему массового обслуживания (рис. 2).

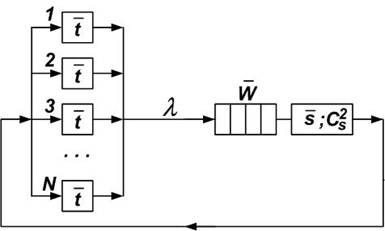
Рис. 2. Модель процесса обработки большого файла

N – количество процессорных ядер в кластере;

  – среднее время обработки блока данных процессорным ядром;

  – среднее время ввода-вывода блока данных дисковым массивом;

– квадратичный коэффициент вариации времени ввода-вывода блока данных дисковым массивом;

λ – интенсивность потока запросов, циркулирующих в системе;

 – среднее время ожидания в очереди к дисковому массиву.

 Пусть в процессе решения прикладной задачи требуется M циклов обработки данных в кластере. Тогда общие средние затраты времени  на обработку данных в кластере с N процессорными ядрами определяются соотношением:

=M.                                                                                                         (1)

Пусть  – средняя задержка в дисковом массиве, которая складывается из времени ожидания   и времени обслуживания , т.е.

 +                                                                                              (2)

Тогда общее среднее время обработки всего объема данных за M циклов равно:

 =  + M  =  M  +M (  + ).                                                     (3)

Качественно общий вид зависимости  от числа процессорных ядер N как суммы двух составляющих, приведен на рис. 3.

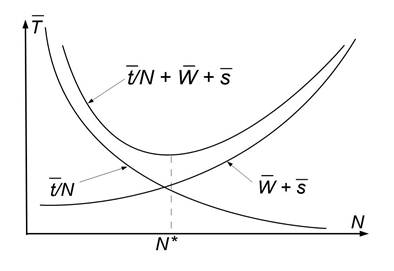
Рис. 3. Общий вид зависимости (N)

         Таким образом, задача сводится к определению значения N^*, при котором функция (N) достигает минимума, т.е.

(N) = M  +M (  + )  ® min                                                         (4)

или

F(N) =  + ® min.                                                                          (5)

Перейдем к определению .

Поток запросов, поступающих на вход дискового массива, представляет собой сумму потоков от большого числа процессорных ядер. Поэтому, с учетом замечания 1, будем считать его пуассоновским. Тогда для приближенного расчета среднего времени ожидания можно использовать формулу Поллачека-Хинчина [19]:

 ≈  ,                                                                                           (6)

где ρ=λ.

Для приближенного определения зависимости значения интенсивности λ от N воспользуемся формулой Литтла [19] для всей системы. С учетом принятых обозначений получим:

N = λ (  +  + ).                                                                                   (7)

Решение данного уравнения с учетом соотношения (6) позволяет найти приближенное значение интенсивности λ и, следовательно, другие средние значения вероятностно-временных характеристик функционирования замкнутой системы (Рис. 2).  Однако, подстановка данного решения в задачу (5) приводит к тому, что расчет значения N^* становится возможным только численными методами. Поэтому продолжим рассуждения.

На рис. 4 приведен общий вид зависимости интенсивности потока l от N в замкнутой системе:

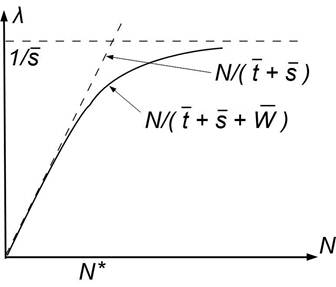
Рис. 4. Общий вид зависимости l(N) в замкнутой системе

С учетом замечания 1 в качестве аппроксимации искомой зависимости l(N) в диапазоне до N^* предлагается использовать функцию

l(N) ≈ .                                                                                               (8)

Для упрощения дальнейших преобразований введем следующее обозначение:

ξ =  .                                                                                                     (9)

В работе [20] приведены результаты исследования распределения времени обслуживания запроса в дисковом массиве, которые показали, что ≈0,15. С учетом данного результата, введенного обозначения ξ и соотношений (6) и (8),   задача (5) после стандартных алгебраических преобразований принимает вид:

F(N) = ξ/N + ® min.                                                                    (10)

Для нахождения минимума функции F(N), т.е. искомого значения N^*,  необходимо решить уравнение

 = 0 ;                                                                                                 (11)

 = 0.                                                                                  (12)

 После стандартных преобразований получим:

N^* = .                                                                                    (13)

Поскольку для рассматриваемого класса задач , то ξ  Поэтому расчетное соотношение можно упростить:

N^* ≈ 0,57 ξ = 0,57 .                                                                             (14)

Полученное соотношение является весьма простым, т.е. внешне вполне удовлетворяет замечанию 2, но вряд ли может быть использовано практически, так как определение значений  и сопряжено с очевидными трудностями.

2.2. Определение исходных данных для расчета

Пусть объем данных, который загружается в кластер с дискового массива и записывается обратно после обработки равен V Mбайт. Пусть дисковый массив показывает производительность P_SPC Mбайт/с по стандартному тесту производительности SPC-2 (www.spcresults.org; Large File Processing) или по любому другому доступному аналогичному тесту. Тогда среднее время  ввода-вывода одного блока данных определяется соотношением:

 = V/P_SPС.                                                                                               (15)

Введем понятие удельной трудоемкости Q прикладной задачи, которую определим как число операций с плавающей точкой, требующихся ядру процессора на обработку 1 байта ввода-вывода данных. Тогда общее количество операций с плавающей точкой G для обработки блока данных объема V будет равно VQ. Если ядро процессора имеет производительность C_LINPACK flops по тесту LINPACK, то время, необходимое такому ядру для обработки объема V может быть вычислено:

 = VQ/C_LINPACK .                                                                                      (16)

С учетом (15) и (16)  соотношение (14) принимает вид:

N^*≈ 0,57 QP_SPC/C_LINPACK .                                                                                  (17)

Таким образом, задача свелась к определению значения удельной трудоемкости Q, но это нужно сделать только один раз для каждой прикладной задачи.

2.3. Математическая модель комплекса с параллельной  системой хранения

Как было отмечено ранее, для повышения пропускной способности дискового массива используются параллельные системы хранения, работающие под управлением  параллельной файловой системы. Поскольку параллельная система хранения осуществляет балансировку нагрузки между своими модулями, в качестве математической модели предлагается использовать замкнутую сеть массового обслуживания, представленную на рис. 5.

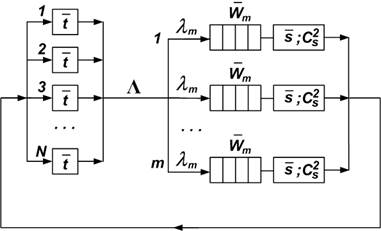
Рис. 5. Модель процесса обработки большого файла с использованием параллельной файловой системы

N – количество процессорных ядер в кластере;

  – среднее время обработки блока данных процессорным ядром;

  – среднее время ввода-вывода блока данных дисковым массивом;

– квадратичный коэффициент вариации времени ввода-вывода блока данных дисковым массивом;

m – количество параллельно работающих модулей в системе хранения;

Λ – интенсивность потока запросов, циркулирующих в системе;

l_m – интенсивность потока запросов, поступающих на вход каждого модуля системы хранения; λ_m = Λ/m;

 – среднее время ожидания в очереди к каждому модулю дискового массива.

 Для определения , как и ранее, будем использовать формулу Поллячека-Хинчина, в которой интенсивность потока запросов λ_m по аналогии с (8) будет определяться соотношением

l_m(N) ≈ .                                                                                         (18)

С учетом принятых обозначений аналогично (5) получим:

F_m(N) =  + ® min.                                                                                (19)  

Для нахождения минимума функции F_m(N), т.е. искомого значения N^*,  необходимо решить уравнение

 = 0;                                                                                                (20)

 = 0.                                                                            (21)

 После стандартных преобразований получим:

N^* = .                                                                                 (22)

По-прежнему для рассматриваемого класса задач , и расчетное соотношение можно упростить:

N^* ≈   = .                                                                  (23)

С учетом введенного понятия удельной трудоемкости прикладной задачи Q соотношение (23) принимает вид:

N^*≈ QP_SPC/C_LINPACK                                                                 (24)  

где P_SPC  -  пропускная способность одного модуля параллельного дискового массива.

Легко видеть, что при m=1 соотношение (24) совпадает с (17).

2.4. Учет  влияния пропускной способности локальной сети

Рассмотрим вопрос использования низкоскоростной локальной сети для подключения кластера к дисковому массиву. В этом случае узким местом в комплексе станет именно сеть, и ее пропускную способность P_LAN  нужно использовать в соотношении (24) вместо пропускной способности массива.

Отметим, что передача информации по сети осуществляется  кадрами фиксированного размера, т.е. =0. Это приводит к некоторой (незначительной) коррекции расчетного соотношения, которой, учитывая замечание 1, можно пренебречь:

N^*≈ QP_LAN/C_LINPACK  .                                                     (25) 

Рассмотрим случай примерного равенства пропускной способности каждого модуля дискового массива и локальной сети, т.е. P_SPC≈ P_LAN = P. Математическая модель такого комплекса в виде замкнутой сети массового обслуживания показана на Рис. 6.

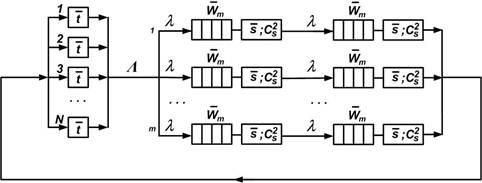
Рис. 6. Математическая модель комплекса при равенстве пропускных способностей локальной сети и дискового массива

В этом случае задача (4) принимает вид:

F(N) = ξ/N +2∙ ® min.                                                              (26)

 = 0 ;

 = 0.                                                                            (27)

 После стандартных преобразований получим:

N^* = .                                                                                 (28)

С учетом введенных обозначений окончательно получим:

N^*≈ QP/C_LINPACK,                                                                     (29)

где P – пропускная способность сети и одного модуля дискового массива.

3. Результаты исследования

В качестве примера использования полученного соотношения рассмотрим одну из самых распространенных и трудоемких задач в области обработки данных сейсморазведки – Reverse Time Migration (RTM) [13, 21].  В [13] приведены результаты измерения времени решения данной задачи при различных исходных данных.  Вычислительный кластер построен на базе Sun Blade 6048 Modular System на базе Sun Blade X6275. Каждый серверный модуль содержит два сервера c двумя четырехъядерными процессорами Intel Xeon QC X5570, 2.93 GHz. LAN построена на базе Infiniband QDR – 40 Gbit/s.

Для определения параметра C_LINPACK обратимся к списку TOP500 (www.top500.org , June 2010).  

Таблица 1.

Фрагмент списка TOP500, June 2010

Rank	Description	Cores	Rmax (TFlops)
10	Red Sky – Sun Blade X6275, Intel Xeon QC x5570, 2.93 GHz, Infiniband QDR	42 440	433.5
15	Tachuonll – Sun Blade X6275, Intel Xeon QC x5570, 2.93 GHz, Infiniband QDR	26 232	274.8

На основе приведенных данных рассчитаем значение C_LINPACK для одного ядра процессора:

C_LINPACK = R_max / Cores ≈ 10.3 GFlops

В качестве системы хранения в [13] вместо дискового массива используется один из серверных модулей X6275 c встроенными flash-накопителем. Интерфейс подключения – SATA II  с пропускной способностью 300 Мбайт/с. Поскольку пропускная способность LAN (40 Гбит/с) много больше пропускной способности flash-modules, то P_SPC = 300 Mбайт/с. Загрузка данных в серверные модули осуществлялась по протоколу NFS.

В табл. 2 приведены экспериментальные данные [13], которые позволяют увидеть характер изменения времени счета при решении задачи RTM в зависимости от количества процессорных ядер.

Таблица 2.

Зависимость времени счета от числа процессорных ядер для задачи RTM [13]

Nodes	8	12	16	20	24
Processors	16	24	32	40	48
Cores	64	96	128	160	192
Calculation Time (sec); 1243 x 1151 x 1231 points	1362	1027	1003	971	1125
Calculation Time (sec); 2486 x 1151 x 1231 points	-	3877	2348	2062	2310

Для определения удельной трудоемкости Q_RTM воспользуемся следующими данными, приведенными в [13].

При использовании одного процессорного узла время счета составило 842 секунды (125 x 1151 x 1231 points), из которых 20 секунд занял процесс инициализации (начальной настройки комплекса), т.е. время решения задачи заняло 822 секундам. Общий объем загруженных в узел данных составил 920 Mбайт. Поскольку очередь к системе хранения при одном счетном узле практически отсутствует, а время ввода-вывода данных составляет  всего несколько секунд, то затраты времени на счет равны примерно 820 секундам. Таким образом, 8 процессорных ядер с производительностью 10300 MFlops  каждое затратили на обработку 920 MByte данных примерно 820 секунд. Следовательно для одного ядра

Q_RTM = ≈ 9200 Flop/Byte

Подставив полученные значения Q_RTM, P_SPC и C_LINPACK в соотношение (17), получим искомое значение границы, до которой целесообразно наращивать число ядер в кластере:

N^*≈ 0,57 Q_RTM P_SPC/C_LINPACK = 0.57 x 9200 x 300 / 10300 ≈ 152            

Поскольку каждый узел содержит 8 процессорных ядер, то целесообразным количеством узлов при решении задачи RTM на заданной конфигурации оборудования является 152/8 = 19, что подтверждается результатами эксперимента, приведенными в табл. 2.

Рассмотрим пример с использованием параллельной системы хранения.

Пусть  комплекс состоит из кластера на базе HP DL360 с процессорами Intel Xeon E5-2680v4, а в качестве системы хранения используется дисковый массив ISILON X210, состоящий из четырех модулей. Согласно данным производителя [15], система хранения ISILON X210 масштабируется линейно до 144 модулей и достигает пропускной способности 200 Гбайт/с, т.е. каждый блок обеспечивает примерно 1380 Mбайт/с.

Таблица 3.

Фрагмент списка TOP500, November 2017

Rank	Description	Cores	Rmax (TFlops)
258	Cluster Platform DL360, Xeon E5-2680v4 14C 2.4GHz, 10G Ethernet	37,884	852.8
271	Cluster Platform DL360, Xeon E5-2680v4 14C 2.4GHz, 10G Ethernet	36,736	831.9

На основе приведенных данных рассчитаем значение C_LINPACK для одного ядра процессора:

C_LINPACK = R_max / Cores ≈ 18,5 GFlops

Поскольку подключение каждого модуля массива осуществляется двумя интерфейсами 10 Gigabit Ethernet с общей пропускной способность P_LAN ≈ 2500 Мбайт/с, т.е. пропускная способность сети примерно в 2 раза выше пропускной способности массива, для расчета следует использовать соотношение (24).

Подставив полученные значения Q_RTM, P_SPC и C_LINPACK в соотношение (24), получим искомое значение границы, до которой целесообразно наращивать число ядер в кластере:

N^*≈ QP_SPC/C_LINPACK = 0.4 x 4 x 9200 x 1380 / 18500 ≈ 1100 cores

Поскольку каждый узел содержит 28 процессорных ядер, то целесообразным количеством узлов при решении задачи RTM на заданной конфигурации оборудования является 1100/28 = 39.

Если же подключение модулей массива осуществить через один интерфейс 10GE, то P_SPC ≈ P_LAN ≈ 1250 Мбайт/с, и для расчета следует использовать соотношение (25), что дает следующий результат:

N^*≈ QP/C_LINPACK  = 0.32 x 4 x 9200 x 1250 / 18500 ≈ 880 cores,

т.е. в этом случае   оптимальная конфигурация кластера будет содержать 31 узел.

4. Заключение

Предложено простое соотношение, позволяющее определить границу, до которой целесообразно увеличивать количество ядер в вычислительном кластере при обработке больших файлов информации в задачах HPC. За счет введения понятия удельной трудоемкости задачи (количество операций с плавающей точкой на один байт ввода-вывода данных), которую требуется определить один раз для заданного класса задач, в качестве исходных данных для расчета удалось использовать значения стандартных тестов производительности LINPACK и SPC-2 Large File Processing (или аналогичный).

Данное соотношение имеет вид:

N^*≈ QP_SPC/C_LINPACK ,                                                               (30)

если пропускная способность локальной сети больше пропускной способности массива;

N^*≈ QP_LAN/C_LINPACK ,                                                              (31)

если пропускная способность локальной сети меньше пропускной способности массива;

N^*≈ QP/C_LINPACK,                                                                     (32)    

если пропускная способность локальной сети примерно равна пропускной способности массива.

Сравнение результата применения полученного соотношения с доступными результатами экспериментальных измерений показало адекватность предложенной модели и целесообразность ее практического использования.

В процессе расчета количества   узлов в кластере следует производить округление в меньшую сторону до реально допустимых значений, так как вблизи значения N^* увеличение количества ядер практически не изменяет время счета, но увеличивает стоимость оборудования.  

References

1. Yuzhu Wang  Y.,  Jinrong Jiang J., Zhang J. et al.  (2018)  An efficient parallel algorithm for the coupling of global climate models and regional climate models on a large-scale multi-core cluster. The Journal of Supercomputing, Volume 74, Issue 8, pp 3999–4018, https://doi.org/10.1007/s11227-018-2406-6

2. Said I., Fortin P., Lamotte J-L., Calandra H. (2017) Leveraging the accelerated processing units for seismic imaging: A performance and power efficiency comparison against CPUs and GPUs. The International Journal of High Performance Computing Applications, Online publication date: 5-Apr-2017.
https://doi.org/10.1177/1094342017696562

3. Yi Li Wang Y.L., Kim K.T., Lee B., Youn H.Y. (2018) A novel buffer management scheme based on particle swarm optimization for SSD. The Journal of Supercomputing, Volume 74, Issue 1, pp 141–159. https://doi.org/10.1007/s11227-017-2119-2

4. Jamiy E., Daif A., Azouazi M., Marzak A. (2015) An Effective Storage Mechanism for High Performance Computing (HPC).  International Journal of Advanced Computer Science and Applications(IJACSA), Volume 6,  Issue 10,  pр 186-188. https://doi.org/10.14569/IJACSA.2015.061026

5. Son S.W., Sehrish S., Liao W., et al. (2017) Reducing I/O variability using dynamic I/O path characterization in petascale storage systems. The Journal of Supercomputing, Volume 73, Issue 5, pp 2069–2097. https://doi.org/10.1007/s11227-016-1904-7

6. Lee S., Hyun  S.J., Kim H-Y., Kim Y-K. (2018) APS: adaptable prefetching scheme to different running environments for concurrent read streams in distributed file systems. The Journal of Supercomputing, Volume 74, Issue 6, pp 2870–2902. https://doi.org/10.1007/s11227-018-2333-6

7. Lee S., Hyun  S.J., Kim H-Y., Kim Y-K. (2018) Fair bandwidth allocating and stripaware prefetching for concurrent read streams and striped RAIDs in distributed file systems. The Journal of Supercomputing, Volume 74, Issue 8, pp 3904–3932. https://doi.org/10.1007/s11227-018-2396-4

8. Hanani  A., Rahmani  A.M., Sahafi  A. (2017)  A multi-parameter scheduling method of dynamic workloads for big data calculation in cloud computing. The Journal of Supercomputing, Volume 73, Issue 11, pp 4796–4822. https://doi.org/10.1007/s11227-017-2050-6.

9. Hadian A., Shahrivari S. (2014) High performance parallel-means clustering for disk-resident datasets on multi-core CPUs. The Journal of Supercomputing, Volume 69, Issue 2, pp 845–863. https://doi.org/10.1007/s11227-014-1185-y

10. Ahmad S.G., Liew  C.S., Rafique M., Munir E.U. (2017) Optimization of data intensive workflows in stream-based data processing models. The Journal of Supercomputing, Volume 73, Issue 9, pp 3901–3923.  https://doi.org/10.1007/s11227-017-1991-0

11. Weichen W., Jing G., Rui C. (2016)  Survey of Big Data Storage Technology. Internet of Things and Cloud Computing, Volume 4, Issue 3, pp 28-33. https://doi.org/10.11648/j.iotcc.20160403.13

12. d’Auriol B.J. (2017) High-bandwidth flexible interconnections in the all-optical linear array with a reconfigurable pipelined bus system (OLARPBS) optical conduit parallel computing model. The Journal of Supercomputing, Volume 73, Issue 2, pp 900–922. https://doi.org/10.1007/s11227-017-1957-2

13. McDade M. (2009) Sun C48 & Lustre fast for seismic RTM using Sun X6275. Oracle Blogs. https://blogs.oracle.com/bestperf/sun-c48-lustre-fast-for-seismic-reverse-time-migration-using-sun-x6275

14. Mills R.T., Sripathi V., Mahinthakumar G. et al. (2010) Engineering PFLOTRAN for scalable performance on Cray XT and IBM BlueGene architecture. Argonne National Laboratory. http://www.mcs.anl.gov/publication/engineering-pflotran-scalable-performance-cray-xt-and-ibm-bluegene-architectures 

15. Isilon X-series.  https://www.emc.com/collateral/software/specification-sheet/h10639-isilon-x-series-ss.pdf

16. Panasas Activestor  Performance Scale-Out NAS Architectural Overview. https://www.panasas.com/resources/whitepapers/scale-out-nas-architectural-overview/

17. Liu  X., Li S., Tong W. (2015) A queuing model considering resources sharing for cloud service performance. The Journal of Supercomputing, Volume 71, Issue 11, pp 4042–4055. https://doi.org/10.1007/s11227-015-1503-z

18. Shen C., Tong W., Hwang J-N., Gao Q. (2017) Performance modeling of big data applications in the cloud centers. The Journal of Supercomputing, Volume 73, Issue 5, pp 2258–2283. https://doi.org/10.1007/s11227-017-2005-y

19. Kleinrok L.   Queuing Systems. Volume 1. Theory. John Wiley & Sons, New York, 1975.

20. Librecht A (2009)  Queueing network models of zoned RAID systems performance. Imperial College London. http://www.doc.ic.ac.uk/~wjk/publications/lebrecht-2010.pdf

21.  Symes W.W. (2007). Reverse time migration with optimal checkpointing. GEOPHYSICS, Volume 72, Issue 5, pp 213-221.

https://doi.org/10.1190/1.2742686