BC/NW 2021№ 1 (37):11.2  

ИСПОЛЬЗОВАНИЕ МАТРИЦ ГИЛЬБЕРТА В ХЕШ-ФУНКЦИЯХ ДЛЯ ПОВЫШЕНИЯ ИХ КРИПТОСТОЙКОСТИ

Голов Д. В., Оцоков Ш. А.

В области численного анализа число обусловленности функции по отношению к аргументу измеряет, насколько может измениться выходное значение функции при небольшом изменении входного аргумента. Причина появления больших погрешностей при решении плохо обусловленных систем хорошо иллюстрируется на примере СЛАУ с двумя неизвестными. Графическое изображение СЛАУ с различными числами обусловленности представлено на рис. 1

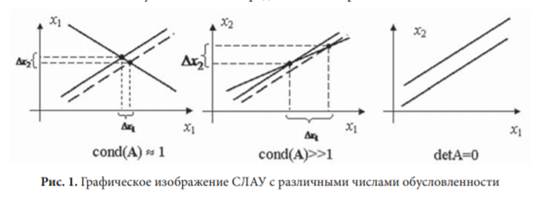
Типичным представителем семейства плохо обусловленных матриц является матрица Гильберта. Особенностью этого типа матриц является то, что операция получения обратной матрицы крайне чувствительна к  изменениям аргументов. Это свойство матрицы Гильберта может быть использовано для повышения криптостойкости хеш-функций, что является одним из основных требований к хешфункциям: малое изменение входных данных должно приводить к значительному изменению выходных. Одной из  проблем некоторых хеш-функций является то, что для последовательно идущих входных данных хеш-функция генерирует последовательно идущие хеши, что значительно понижает криптостойкость хеш-функции. Для повышения криптостойкости входные данные могут служить «возмущением» в матрице Гильберта, затем операция инвертирования матрицы Гильберта позволит получить значительно измененные входные данные для стандартной хеш-функции. Таким образом последовательно идущие входные данные будут явно изменены.

Литература

1. Фадеев Д. К. Вычислительные методы линейной алгебры: Электронно-библиотечная система издательства Лань, 2009 2

2. . Ростовцев А. Г., Маховенко Е. Б. Теоретическая криптография, 2004