BC/NW 2021№ 1 (37):7.1
ИССЛЕДОВАНИЕ ИМИТАЦИОННОЙ МОДЕЛИ УЗЛА СЕТИ ПРИ РАЗЛИЧНЫХ РАСПРЕДЕЛЕНИЯХ ПОТОКА ВНЕШНИХ ЗАПРОСОВ
Данилин Д.Г., Манов А.С
Проектирование крупной сети со сложной топологией в настоящее время не обходится без имитационного моделирования, которое необходимо при определении точных данных о количестве требуемого оборудования, а значит, и затрат на него. При этом имеет большое значение точность результатов моделирования, так как в конечном итоге она сказывается на определении затрат.
Целью данной статьи является исследование модели узла сети на предмет требуемого оборудования в зависимости от входной нагрузки на сеть, а именно числа серверов от частоты поступления запросов пользователей. Исследование будет производиться на имитационной модели узла сети при двух различных зависимостях входного потока заявок на сеть (стандартном Пуассоновском распределении и вероятностном распределении Парето, более подходящим при моделировании NGN).
Можно считать обоснованным мнение специалистов, разрабатывающих сети стандарта NGN , что телекоммуникационный трафик в сетях нового поколения для основной массы Web-сервисов представляет собой так называемый самоподобный (фрактальный) поток, или же обладает свойством самоподобия. Передача различных данных в виде пакетов информации потребовала с новой точки зрения взглянуть на алгоритмы анализа сетевого трафика, связанные, в первую очередь, с описанием и классификацией входных потоков и аналитическим расчетом нагрузки на реализуемую сеть в связи с проявлением описанного выше свойства самоподобия в трафике сети.
А именно, классический аппарат по анализу сетевого траффика, основанный на экспоненциальных потоковых моделях (Пуассона), даёт достаточно точную оценку параметров, но применим только в ныне устаревших сетях коммутации каналов (известных также, как телефонные сети). В то время как в компьютерных сетях нового поколения данный принцип даёт весьма неточную (зачастую весьма оптимистичную) оценку состояния системы.
Описанные выше проблемы накладывают существенные ограничения на параметры при моделировании сетевых структур, а именно входной поток клиентских заявок на маршрутизатор моделируемого узла сети не может иметь экспоненциальное распределение, в виду принципиального различия в точности работы модели и реальной сети.
Понятие самоподобного потока
Для дальнейшего определения распределения Парето необходимо объяснить суть самоподобного входного потока (как было сказано ранее, трафик сетей стандарта NGN имеет фрактальную составляющую, или же является самоподобным). Рассмотрим сущность самоподобия более детально.
Простейшими самоподобными объектами являются фракталы. С точки зрения математики фрактал – это так называемое множество с дробной размерностью. По этой причине принято процессы, обладающие свойством самоподобия, называть фрактальными (по причине представления в виде дискретных наборов элементов в множествах).
Поток событий, что вполне логично, может обладать свойством самоподобия. Существует несколько подходов в формировании самоподобного потока.
Рассматриваемый метод имеет свое основание исходя из того, что рассматривается суперпозиция («суммарное» влияние) сразу нескольких (находящихся в чередующейся последовательности) независимых между собой и имеющих один и тот же закон распределения источников, временные интервалы наступления событий в периодах которого обладают так называемым эффектом Ноа. Под строгим чередованием источников подразумевается модель, где периоды однозначно расположены в порядке чередования, при этом длительности одной группы периодов полностью независимы, а также имеют идентичное распределение, и длительности периодов другой условной группы также независимы и аналогично подчиняются одинаковому закону распределения. Но при этом обязательным условием является тот факт, что последовательности длительностей обоих групп периодов никак не зависят друг от друга и не пересекаются.
Также стоит учесть, что при этом длительности различных периодов теоретически могут иметь различные распределения. Свойство эффекта Ноа применимо к распределению длительностей периодов – базовая установка создания модели самоподобного трафика (в отличие от привычных моделей, в которых применяется стандартное экспоненциальное распределение). Эффект Ноа также, в некоторых источниках, именуется аналогом «синдрома бесконечной дисперсии», который появился вследствие эмпирических наблюдений того, что большинство природных явлений можно описать, как распределение с бесконечной дисперсией. Для математической реализцаии эффекта Ноа и достижения сопутствующих свойств вполне можно использовать вероятностное распределение Парето, либо логарифмически-нормальное распределение случайной величины.
Ключевым отличием от экспоненциально распределённого потока является «затухание» зависимости по степенному закону.
Касательно нашей задачи, для достижения свойства самоподобия входного потока заявок на узел сети будет использоваться аналогичное свойство распределения Парето. Также в процессе исследования будет произведен сравнительный анализ результирующих искомых кривых, распределенных по экспоненциальному и распределению Парето соответственно.
Распределение Парето
Под распределением Парето в теории вероятностей принято называть целое множество абсолютно непрерывных распределений, являющихся в свою очередь степенными.
На практике, в реальных задачах зачастую можно встретить так называемые усеченные распределения, или же распределения, множества значений случайной величины которых ограничены значением некоторого порогового уровня С0. Например, таковое распределение будет иметь случайная величина (её переменная) в том случае, если ее значение не будет опускаться ниже некоторой заданной величины.
Распределение Парето – вероятностное распределение случайной величины, для которого функция и плотность распределения вероятностей имеют вид:
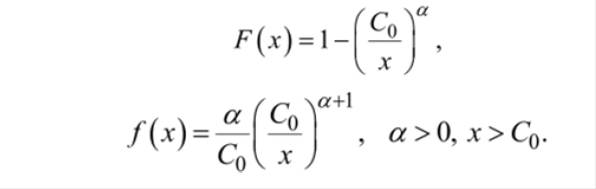
Можно проследить, что плотность распределения вероятности монотонно убывает, выходя из точки С0.
Вычислим математическое ожидание такой случайной величины:
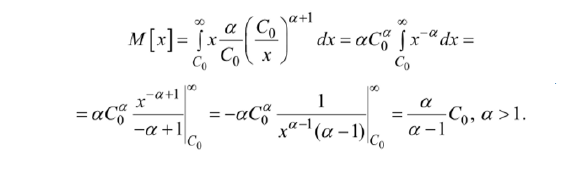
Соответственно для дисперсии получим выражение:
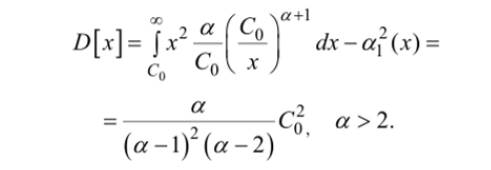
Как можно заметить, с ростом случайной величины распределение начинает «вырождаться» (дисперсия случайной величины начинает стремиться к некоторому пороговому постоянному значению). В этом заключен один из принципов самоподобия.
Также стоит упомянуть, что помимо самоподобия и «затухания хвоста зависимости», распределение Парето обладает еще рядом примечательных свойств, что допускает его применение в широком спектре исследований. Перечисление таковых свойств в данной работе не будет представлено ввиду того, что для построения входного потока с заданным распределением вполне достаточно ограничиться свойством самоподобия.
Разработка и программная реализация модуля диспетчеризации внешних запросов в вычислительной сети.
Данный модуль выполняет следующие функции:
1. Имитирует поток входящих заявок, распределенный по Пуассону и Парето. Параметры законов распределения: математическое ожидание и дисперсия, определяющие интенсивность потока заявок, задаются пользователем. Также пользователь задает количество клиентов и пропускную способность сервера (время обработки одной заявки).
2. При этом все пространство IP адресов разбивается на N равных частей, и каждая часть закрепляется за одним из N серверов (заявки с этих IP адресов поступают на данный сервер). Для простоты каждой заявке вместо IP адреса ставится в соответствие признак принадлежности к одной из N частей пространства адресов. Признаки также задает пользователь, то есть довольно случайно распределяет клиентов по серверам.
3. Заявки поступают на вход коммутатора (модуля диспетчеризации), который распределяет их по N серверам. Для каждого сервера коммутатор подсчитывает количество пришедших заявок. Время моделирования задается пользователем.
4.Время обслуживания заявки на сервере имеет показательное распределение. Пакет, пришедший на модуль диспетчеризации и заставший хотя бы один сервер свободным, сразу же занимает любой из свободных серверов, где начинается процесс его обслуживания. В случае если все сервера в момент поступления пакета заняты, он помещается в очередь. Из очереди пакеты выбираются на обслуживание в соответствии с дисциплиной FIFO (первый пришедший пакет будет обслужен первым освободившимся сервером). Заявка, заставшая все сервера и все места в очереди занятыми, навсегда покидает систему, не оказывая никакого влияния на ее дальнейшее функционирование.
5. Результат фиксируется в выходном текстовом файле, который должен содержать следующую информацию:
- конфигурация моделируемого участка сети (количество клиентов, количество серверов);
- средняя загрузка (для каждого сервера);
- количество превышений загрузки над пропускной способностью (для каждого сервера).
6. По результатам моделирования будет построена зависимость количества необходимых серверов от интенсивности входного потока заявок. Таким образом, можно оценить аппаратные затраты, необходимые для обслуживания клиентов при различной интенсивности их работы.
Метод расчета: для каждого сервера подсчитывается число пришедших заявок. После окончания моделирования для каждого сервера подсчитывается количество превышений загрузки над пропускной способностью. Далее для каждого сервера количество пришедших заявок делится на пропускную способность данного сервера. Результат деления и есть средняя загрузка. А количество превышений загрузки над пропускной способностью делится на количество пришедших заявок и получается количество превышений загрузки над пропускной способностью на заявку.
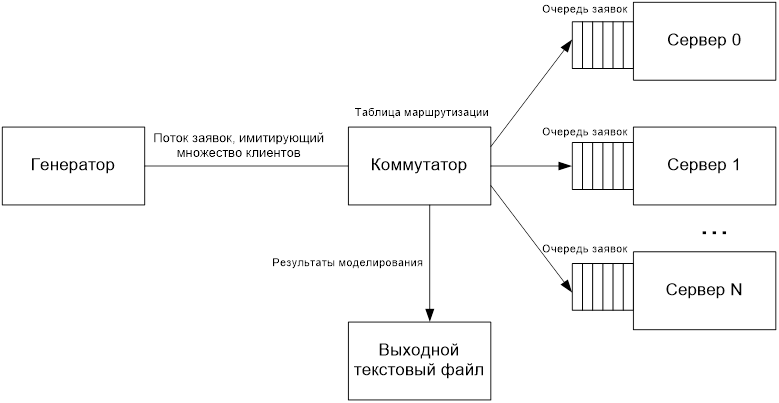
Рисунок 1 - Структурная схема работы разработанной имитационной модели
Поставленная задача решена следующим образом: на языке С# разработана и составлена имитационная модель, которая соответствует по характеристикам оригиналу, то есть коммутатору, но имеет допущение – данный модуль обладает бесконечной пропускной способностью, чего в реальности достичь, естественно, не возможно. Разработанная программа принимает заявки от клиентов, анализирует IP-адрес клиента, и в соответствии с ним передает заявку на обработку тому или иному серверу. Конкретная часть IP-адресов закреплена за определенным сервером. Кроме того, разработанный модуль позволяет анализировать среднюю загрузку каждого из серверов и превышение количества заявок, пришедших на обработку, над пропускной способностью сервера.
Также создан графический интерфейс пользователя для ввода начальных данных для моделирования и просмотра результатов. После окончания моделирования программа модифицирует выходной текстовый файл, записывая в него результаты моделирования.
Исследование состоит в построении зависимости количества серверов от дисперсии потока заявок с использованием разработанной имитационной модели.
Посредством разработанного программного модуля построим графики зависимости необходимого количества серверов от интенсивности потока клиентов.
Моделирование будет происходить при значении математического ожидания случайной величины (интенсивности), равном значению из диапазона [10,4000] мс, и среднеквадратичном отклонении (дисперсии случайной величины), изменяющемся в диапазоне [10, 500] мс.
Зависимость будем строить по следующей методике:
- изначально зафиксируем математическое ожидание клиентского времени;
- при фиксированном математическом ожидании последовательно изменяем значение среднеквадратичного отклонения клиентского времени;
- в случае если очередь поступивших заявок переполняется, добавляем еще один сервер;
- производим перераспределение клиентов и серверов;
- далее фиксируем другое значение математического ожидания и повторяем процесс.
Моделирование, согласно разработанному алгоритму, производится с шагом, равным 50 мс, достаточным для достижения необходимой точности при анализе рассматриваемой системы.
Интервал времени для рассмотрения ограничим 2000 мс. Зависимость при большей длительности моделирования принимает условно установившийся характер и не даёт ценной информации при анализе. В условиях работы максимальное количество серверов, необходимое для работы сети с пренебрежимо малым числом отказов, было принято равным 10, а размер очереди был условно принятой константой размером в 30 заявок. Стоит отметить, что в случае, если обработано 10000 заявок, и при этом число заявок, покинувших систему, не превысило 0,01% от общего числа, то моделирование заканчивается.
Построенные графики для распределения Пуассона и Парето имеют вид:
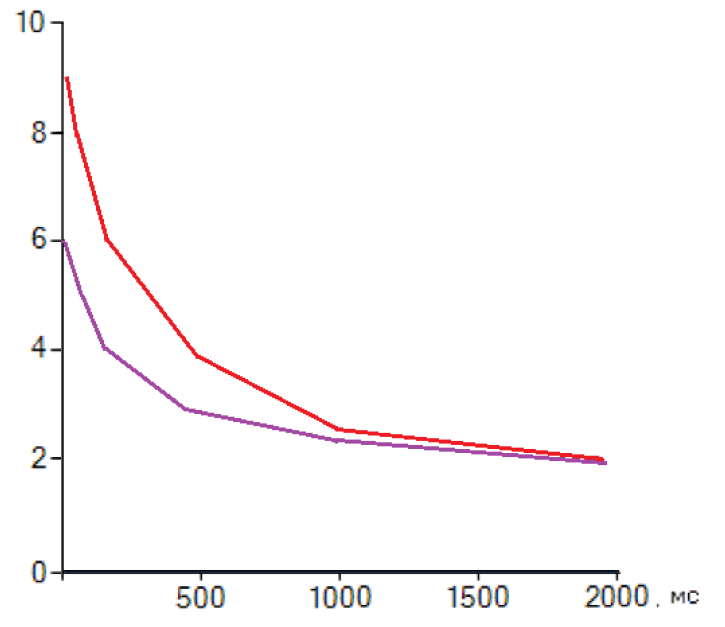
Рисунок 2 – Зависимость количества серверов от интервала поступления заявок
На рисунке 2 красным цветом нам показана экспоненциальная зависимость (кривая расположена выше относительно осей), фиолетовым – кривая распределения функции Парето (кривая расположена ближе к осям).
Как следует из графиков, при моделировании входного потока на узел сети при заданной интенсивности поступления клиентских заявок, в сетях формата NGN рациональнее использовать вероятностное распределение Парето.
Это обусловлено, во-первых свойством самоподобия в вероятностном распределении Парето, схожим с пульсациями информационного потока в современных сетях с пакетной коммутацией, а также большей устойчивостью распределения к обработке пограничных ситуаций при моделировании и реализации алгоритма по нахождению необходимого количества оборудования.
Касательно используемых экспериментальных данных, из графика видно, что при использовании вероятностного распределения Парето требуемое количество условных единиц оборудования сократилось и однозначно умещается в условный полуинтервал (5;6]. Кроме того, график быстрее сходится к устойчивому положению.
Аналогичный алгоритм поиска необходимого количества серверов при экспоненциальном законе распределения входного потока дает менее точные и несколько завышенные результаты, колеблющиеся в интервале (8:10), без четкой верхней границы. Это обусловлено чувствительностью алгоритма и степенной функции к граничным положениям значений интенсивностей при моделировании.
Подводя итог, стоит сказать, что оба типа распределения применимы при анализе и проектировании сетевых структур различного масштаба. Оба подхода позволят оценить необходимую на стадии планирования узла сети аппаратную базу. Но наиболее эффективным из предложенных является подход с использованием вероятностного распределения Парето в качестве закономерности для моделирования входного клиентского потока.
Данный подход более уместен для применения в сетях современного стандарта NGN, т.к. распределение условно учитывает колебания информационного потока, свойственные сетям с коммутацией пакетов данных. Кроме того, данный метод позволит получить более точную количественную оценку необходимого оборудования, что существенно сократит расходы на аппаратные ресурсы проектируемой сети.
Литература
1.Вишневский В.М. Теоретические основы проектирования компьютерных сетей. – М.: Техносфера, 2003. – 512 с.
2. . Треногин Н.Г., Соколов Д.Е. Фрактальные свойства сетевого трафика в клиентсерверной информационной системе. – Новосибирск: Вестник СУВПТ, 2001. - 172 с.
3. Васильев К. К., Служивый М. Н. Математическое моделирование систем связи: учебное пособие. – Ульяновск: УлГТУ, 2008. – 170 с.
4. Шилдт Г. C# 4.0. Полное руководство. – М.:ООО ”И.Д. Вильямс ”, 2019. – 800 с.