BC/NW 2021№ 1 (37):9.1  

РАЗРАБОТКА МОДЕЛИ СВЕРТОЧНОЙ НЕЙРОННОЙ СЕТИ ДЛЯ РАБОТЫ НА НЕРЕГУЛЯРНОМ НОСИТЕЛЕ

Колесников И. Е., Вишняков С. В.

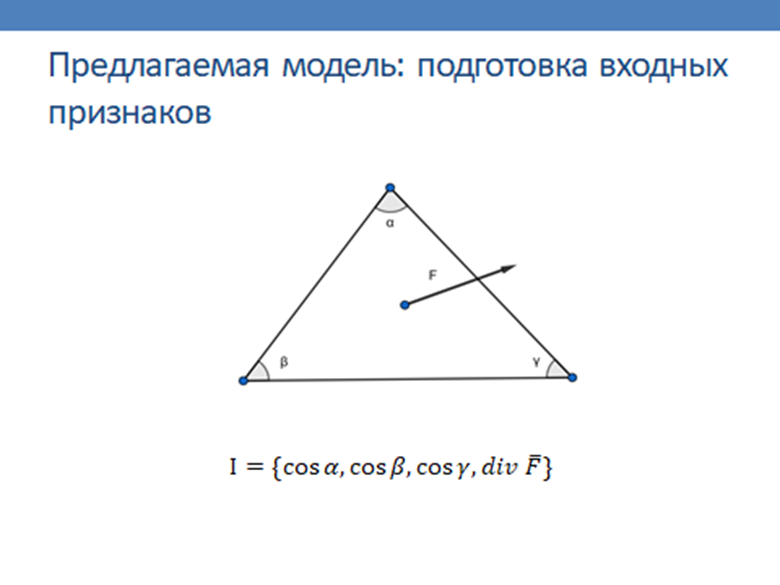
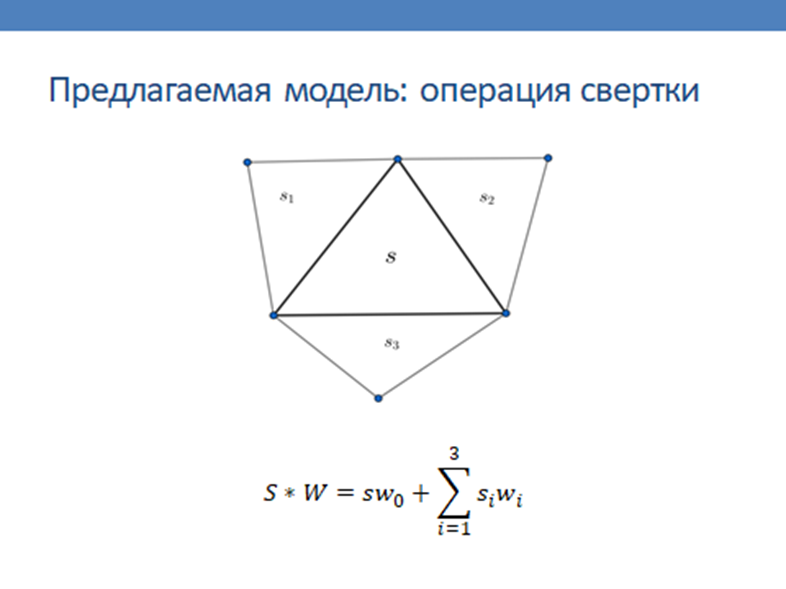
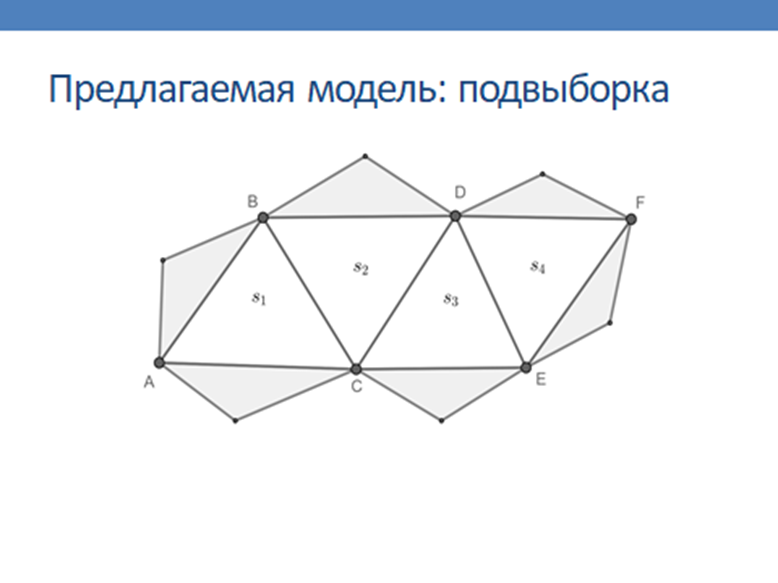
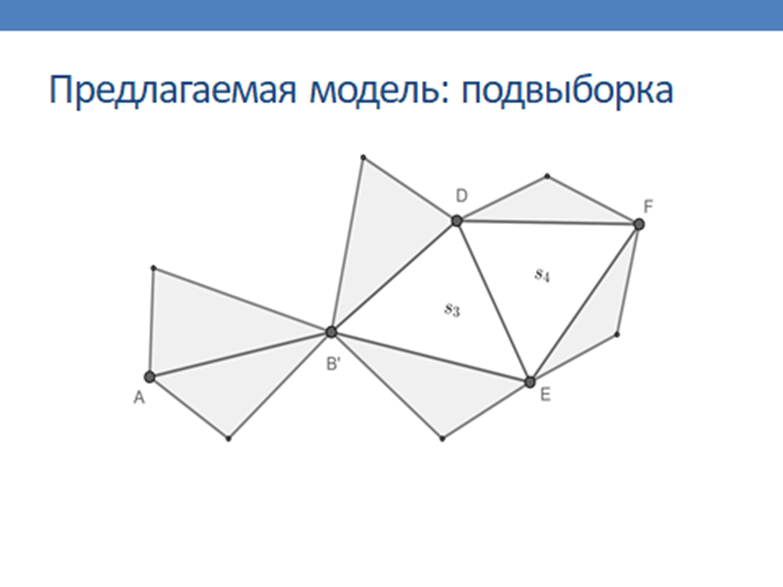
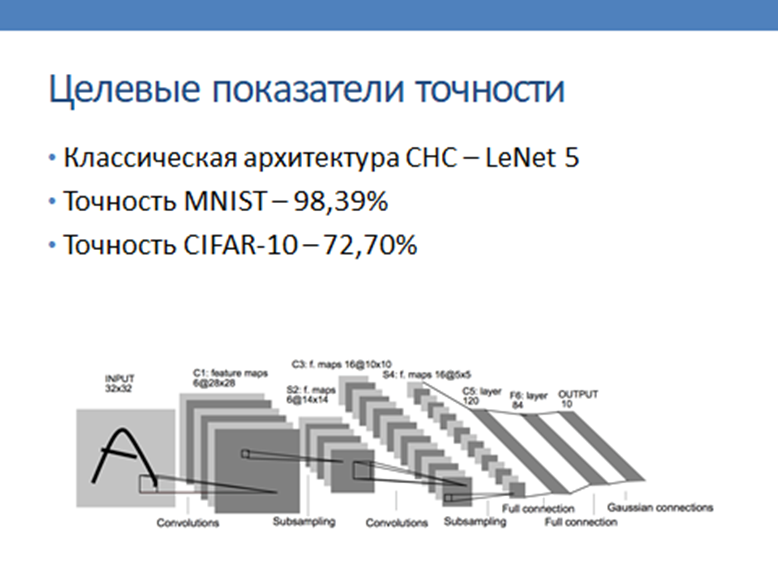
Сверточные нейронные сети являются эффективным инструментом для решения задач анализа графической информации [1]. Однако, классическая сверточная архитектура сети применима только для регулярного графического сигнала. Вместе с тем, на нерегулярных носителях сигнала возникают сходные задачи интеллектуальной обработки сигнала [2]. Существует ряд методов, упрощающих применение сверточной архитектуры для использования на  нерегулярных носителях, однако, данные методы жестко привязаны к специфичным входным признакам сети, и не позволяют использовать векторные и  геометрические характеристики сигнала в  качестве входных признаков. Тем не менее, был найден метод анализа сигнала на основе исключения ребер нерегулярной сетки [3], который лег в основу предлагаемой модели. В данном докладе представляется модель архитектуры сверточной нейронной сети, которая реализует базовые операции сверточных нейронных сетей (свертка, подвыборка и нормализация данных), основываясь на геометрических и векторных характеристиках симплексов сигнала. Согласованность и  равномерность перечисленных операций обеспечивается за счет выбора трех смежных симплексов для каждого рассматриваемого симплекса. По результатам программной реализации данного метода, будут проведены испытания модели на открытых наборах данных по классификации и сегментации изображений.

Литература

1. LeCun Y., Boser B., Denker J. S., Henderson D., Howard R. E., W. Hubbard and L. D. Jackel Backpropagation Applied to Handwritten Zip Code Recognition, Neural Computation, 1989, vol. 1 (4), pp. 541–551

2. Vishnyakov S., Pekhterev V., Sokolova E. A Novel Method of the  Image Processing on Irregular Triangular Meshes // Proc. SPIE 10615, Ninth International Conference on Graphic and Image Processing (ICGIP 2017). doi:10.1117/12.2302961.

3. Hanocka R., Hertz A., Fish N., Giryes R., Fleishman S., and Cohen-Or D. MeshCNN: a network with an edge // ACM Transactions on Graphics (TOG). 2019 Т. 38 №.4 P. 1–12.