BC/NW 2024 № 1 (41):10.1

ПРОБЛЕМА КОЛИЧЕСТВЕННОЙ ОЦЕНКИ ИСКАЖЕННОСТИ ФОТОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ

Нечаев А.А.,. Гольцов А.Г.

Задача оценки качества изображений является актуальной при разработке и тестировании цифровых алгоритмов обработки изображений. [1] Оценка качества изображений может быть необходима и из-за внесения искажений в изображения (например, при хранении или передаче).

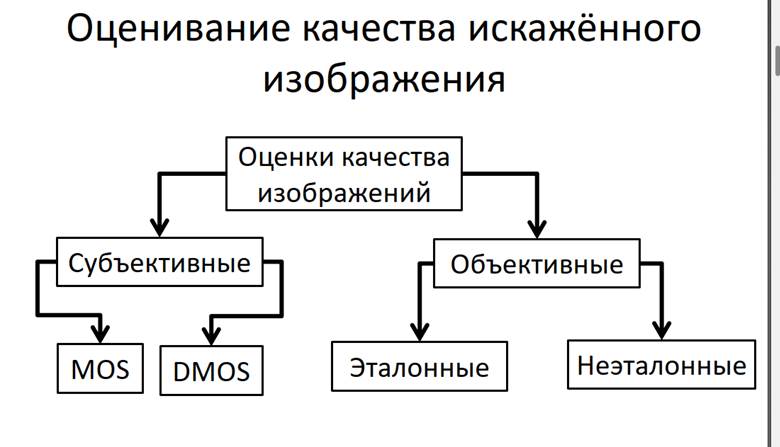
 Возникает вопрос, какие оценки качества изображений являются наиболее правильными. В тех случаях, когда изображения в итоге должны быть показаны людям, единственной "правильной" оценкой является субъективная оценка человека. [2]

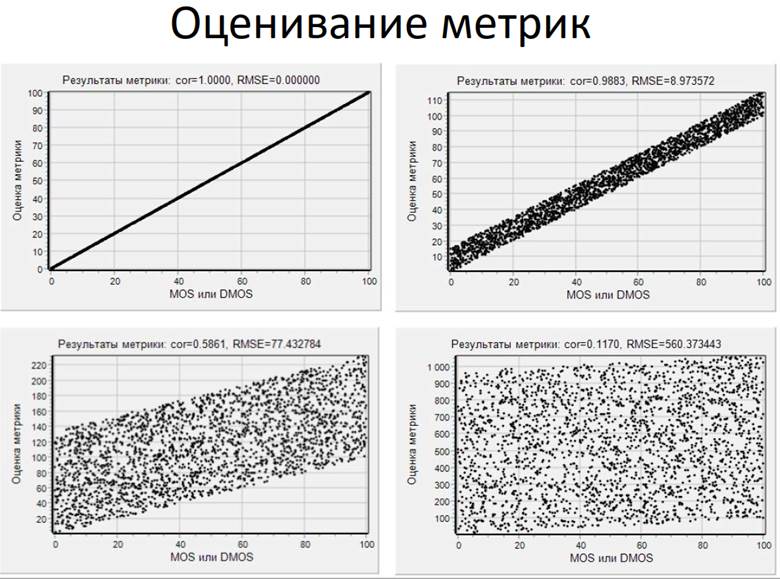
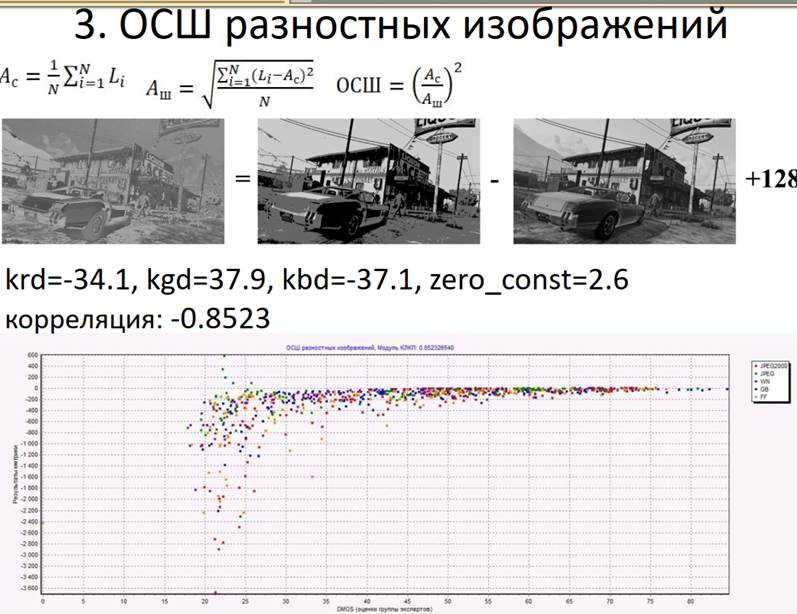
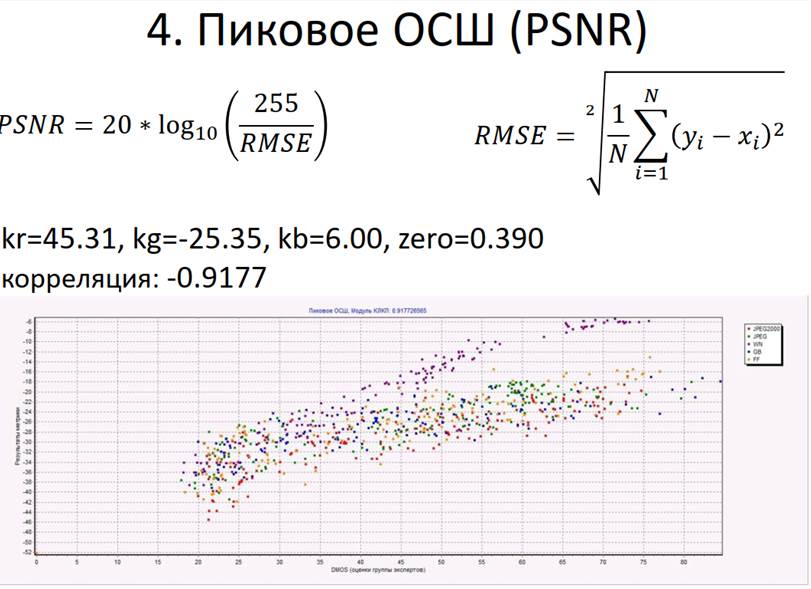
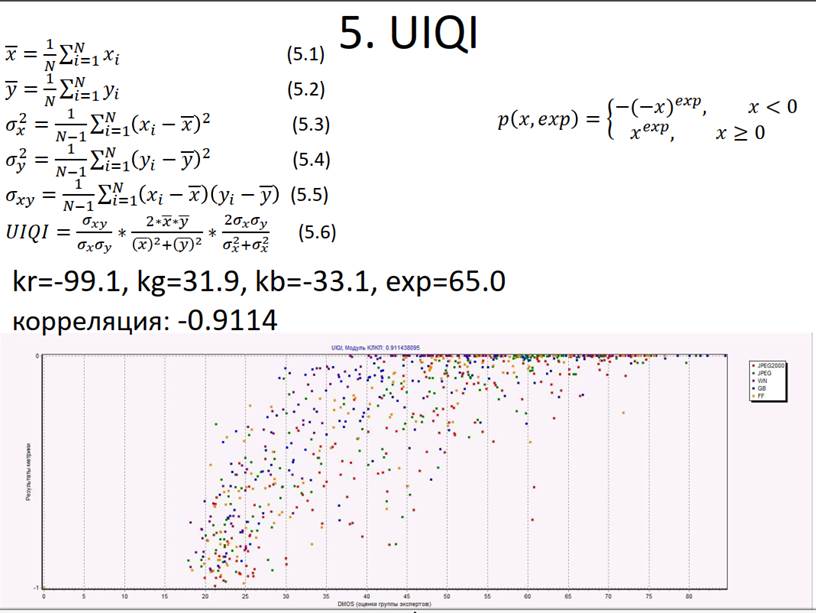
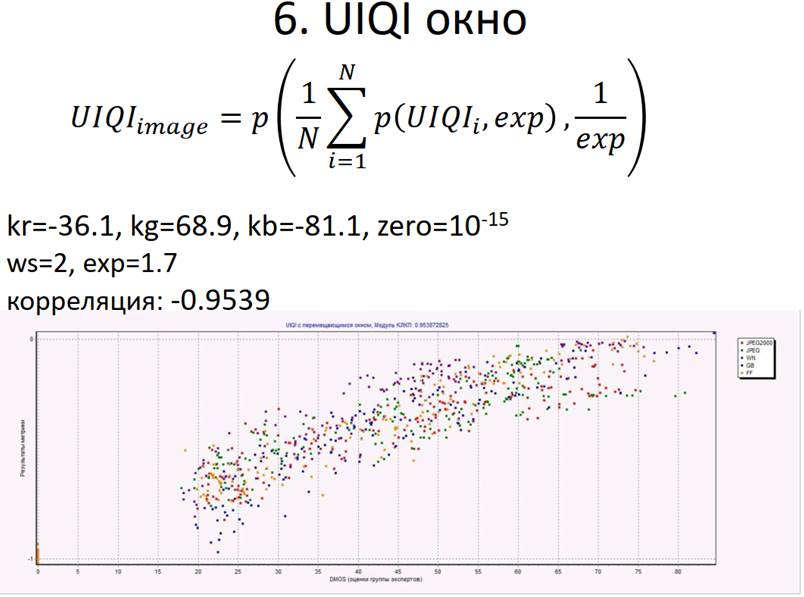
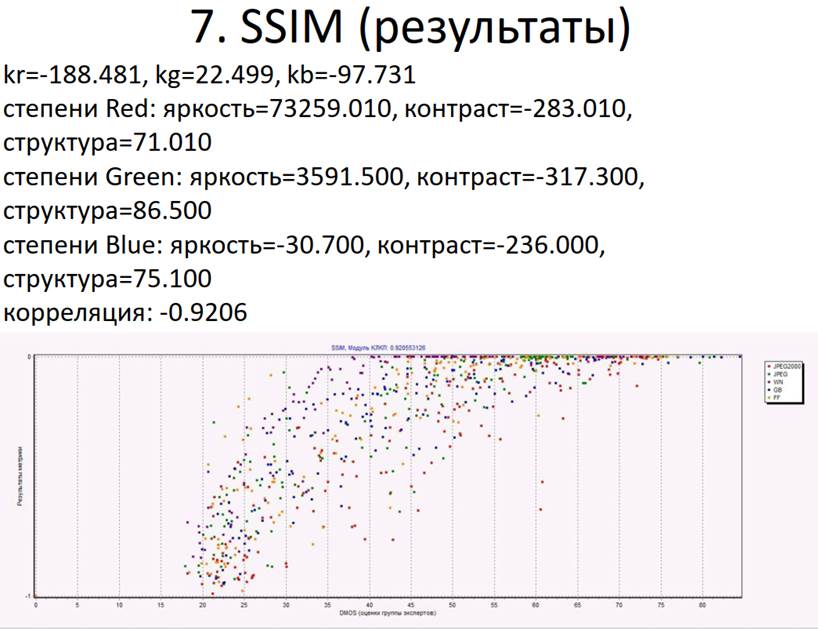
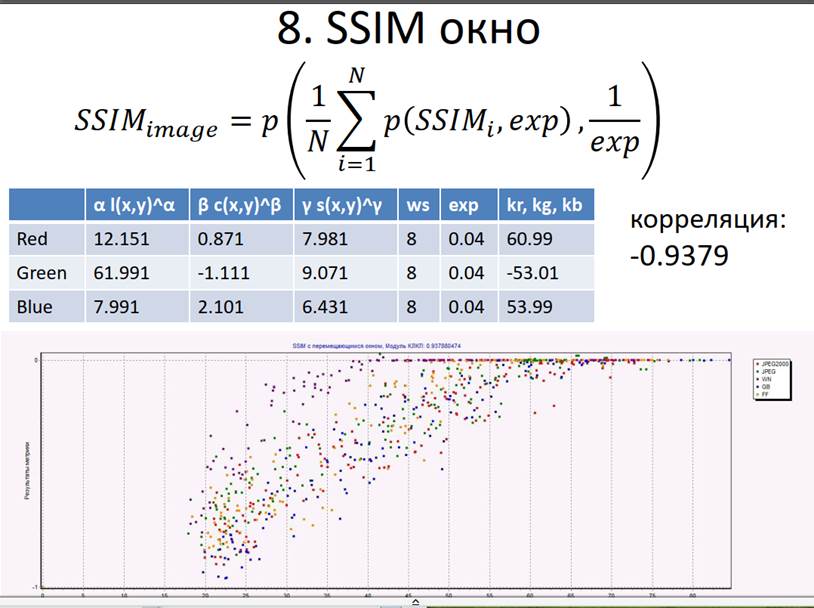
Существуют разные методы оценки качества изображений. В зависимости от метода меняется степень сходства его оценок с оценками человека. Например, некоторые простые методы (MSE, PSNR) дают более далёкие от субъективных оценки [2], методы UIQI и SSIM — более близкие оценки. [3] Однако на данный момент нет метода, который позволял бы давать такие оценки качества изображений, которые бы всегда точно совпадали с оценками человека.

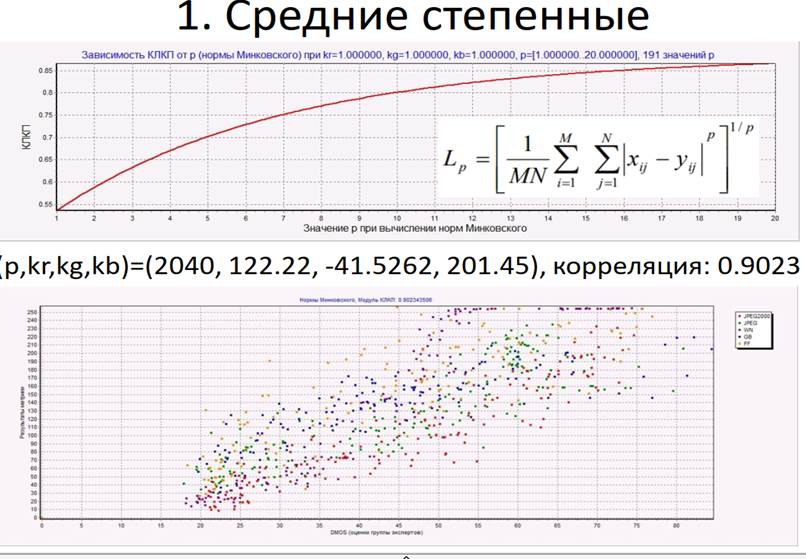
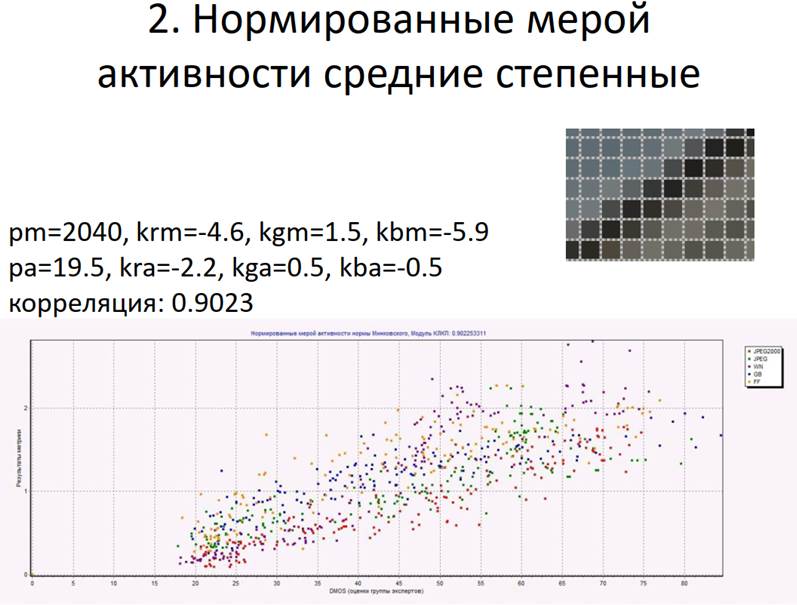
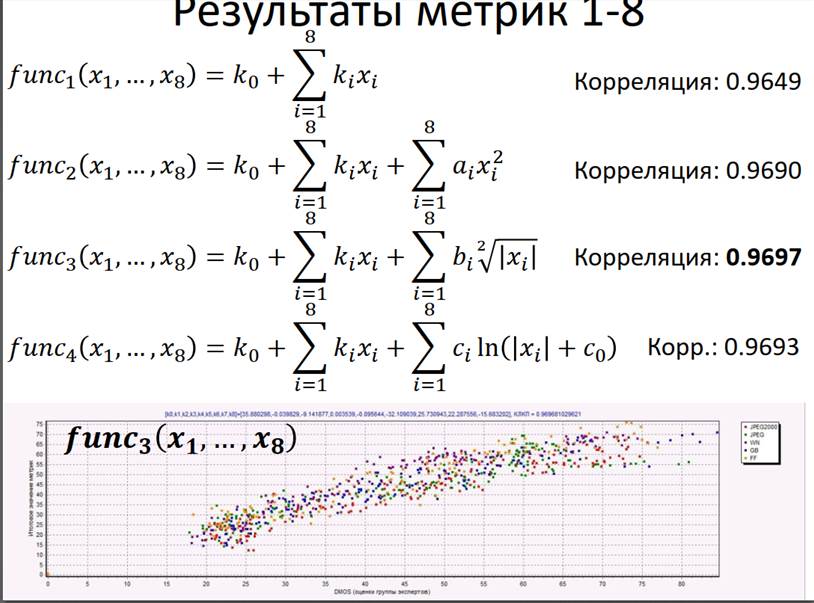
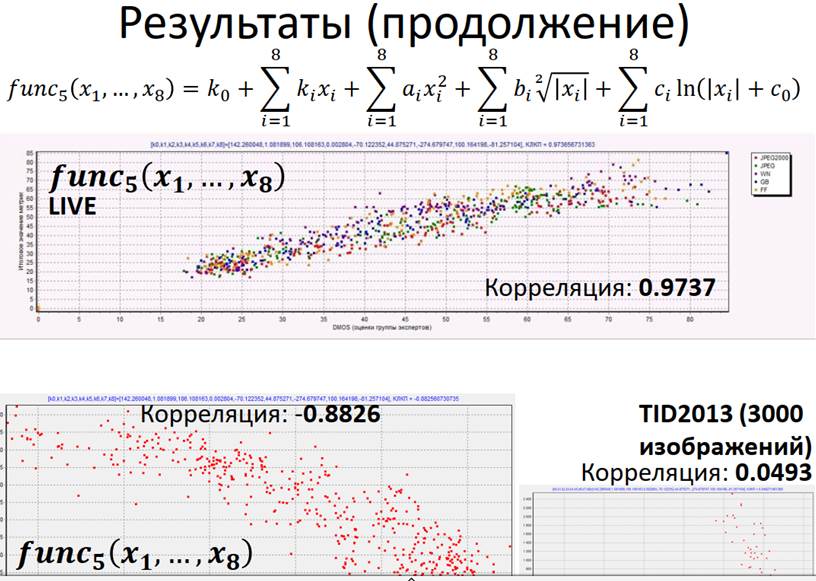
Зрение человека имеет разную чувствительность к искажениям разных типов, поэтому при оценивании качества важен тип искажений. Если тип искажений известен, то корреляция между объективными оценками (метода) и субъективными (человека) сильнее, чем при неизвестном типе искажений. Полученный в результате выявления закономерностей метод оценки качества применим к изображениям только с теми типами искажений, которые использовались при выявлении этих закономерностей. Во многих случаях наиболее близкая к линейной зависимость между оценками метода и оценками человека достигается при вычислении логарифма от полученных значений.

Литература

1. Сидоров Д. В. Модификация алгоритма SSIM // Прикладная информатика, 2010 — №4(28). — 123–125.

2. Z. Wang, A.C. Bovik. A Universal Image Quality Index. IEEE SIGNAL PROCESSING LETTERS, Vol. XX, No. Y, pp. 81-84 (Mar. 2002).

3. Wang Z. Image quality assessment: from error visibility to structural similarity. — IEEE transactions on image processing, vol. 3, 2004, p. 600–612.