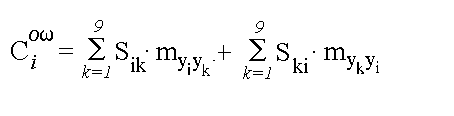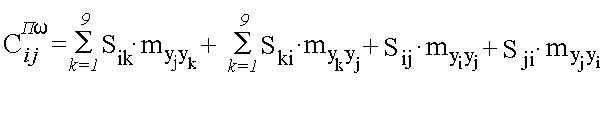РЕШЕНИЕ ЗАДАЧИ «Расчет кратчайшей сети заданной конфигурации»
Л.И. Абросимов,
(г. Москва, Московский
энергетический институт (Технический университет), Россия )
Формулировка
задачи
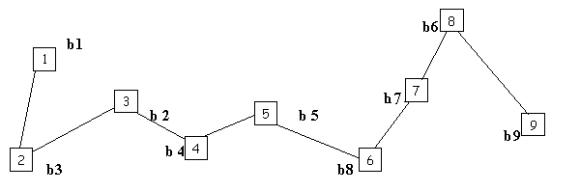
Задана конфигурация сети S-
последовательная двунаправленная шина, дуги которой соединяют узлы ai
1ó2ó3ó4ó5ó6ó7ó8ó9
Конфигурацию
S можно записать в виде матрицы S.
Матрица
S:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
3 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
4 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
5 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
6 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
7 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
8 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|
9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
Рисунок 1
Известно
также распределение точек ba в пространстве:
Расстояния
между точками также записываются в виде матрицы M.
Требуется распределить узлы по точкам ba , размещённым в
пространстве на расстоянии mab друг от друга таким образом, чтобы суммарная взвешенная длина
рассматриваемой сети была минимальной.
Матрица M:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
0 |
15 |
24 |
25 |
50 |
70 |
75 |
60 |
100 |
|
2 |
15 |
0 |
15 |
11 |
35 |
55 |
50 |
48 |
90 |
|
3 |
24 |
15 |
0 |
25 |
50 |
70 |
75 |
60 |
100 |
|
4 |
25 |
11 |
25 |
0 |
25 |
45 |
40 |
35 |
60 |
|
5 |
50 |
35 |
50 |
25 |
0 |
40 |
30 |
26 |
70 |
|
6 |
70 |
55 |
70 |
45 |
40 |
0 |
12 |
30 |
40 |
|
7 |
75 |
50 |
75 |
40 |
30 |
12 |
0 |
18 |
28 |
|
8 |
60 |
48 |
60 |
35 |
26 |
30 |
18 |
0 |
40 |
|
9 |
100 |
90 |
100 |
60 |
70 |
40 |
28 |
40 |
0 |
Рисунок 2
Иначе
говоря, требуется «раскидать шары по лункам».
![]()
![]()
![]()
a1
ai … a9
b1 ba … b9
Рисунок 3
Распределение записывается в
виде списка y таким образом: y={ai}.
В списке перечисляются номера ![]() гнёзд ba , а порядок i их размещения в списке по
номерам i узлов ai. Например,{2, 4, 5….} означает, что 1-й узел сети «положили» во 2-е
гнездо, 2-ой узел – в 4-е гнездо и т. д.
гнёзд ba , а порядок i их размещения в списке по
номерам i узлов ai. Например,{2, 4, 5….} означает, что 1-й узел сети «положили» во 2-е
гнездо, 2-ой узел – в 4-е гнездо и т. д.
Решение
задачи.
Алгоритм
решения.
1. Исходные данные: N=9, || Sij ||, i,j=1,…,N; || mab || , a,b=1,…,N; Начальное значение целевой
функции Q0=∞;
{yi}*= {0} (i=1,…,N), ω =
№ варианта mod 9 = 1 mod 9 = 1
2. Формирование для варианта ω
исходного списка {yi}ω по соотношению (1) для
![]() i=1,…, N:
i=1,…, N:
(i + ω –1) для 1
≤ i ≤ (N –ω +1);
yi ω = (1)
(i + ω – N –1) для i
> (N –ω +1).
3. Расчёт
цен Сi 0ω для i=1,…, N по
соотношению (2) и формирование списка {Сi 0ω}
|
|
(2) |
|
|
|
4. Расчёт цен Сij Пω для i,j=1,…,N по
соотношению (3) и формирование матрицы
||Сij Пω||
|
|
(3) |
5.
Расчёт оценки Qijω по соотношению (4).
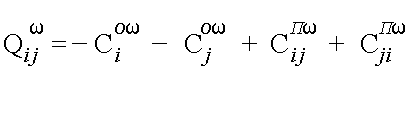
(4)
6. Расчёт минимальной оценки min Q и
фиксирование номеров i*,j*, которые соответствуют min Q.
7. Проверка, если min Q <0,
то перейти к п. 8, иначе – к п. 9.
8. Корректировка исходного списка {yi}ω за счёт перестановок p:=yi* , v:=yj*
yi*:=v ,
yj*:=p и переход к п.3
9. Расчёт Qω по соотношению (5)
N=9 N=9
Qω = ∑
∑ Sij · myi
yj (5)
i=1 j=1
10. Если Qω < Q0, то перейти к п.11, если Qω≥Q0, то перейти к п.12
11. Корректировка оптимального значения целевой
функции Q0 := Qω и списка оптимального
решения {yi}*={yi}ω
12. Корректировка номера исходного варианта ω:=ω+1
13. Если номер исходного варианта ω≤N, то
перейти к п.2, иначе – к п.14
14. Вывод результата расчёта оптимального значения
целевой функции Q0 и списка
оптимального решения {yi}*.
Пример пошагового решения задачи по заданным выше исходным данным, соответствующим П1
Для
иллюстрации представим расположение в пространстве гнезд соответствующее
матрице М следующим образом:
![]()
b6
![]() b1
b1
![]()
![]()
![]() b7
b7
![]() b 2 b 5
b 2 b 5
![]() b9
b9
![]()
![]() b 4
b 4
b3 b8
Рисунок 4
П.2 алгоритма
Для первого варианта ω = 1
y = { 1, 2, 3, 4, 5, 6, 7, 8, 9}
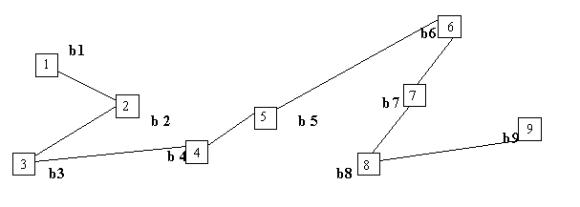
Рисунок 5
П.3 алгоритма
Итерация
1:
С1 01
=S[1,1]*m[1,1] + S[1,1]*m[1,1] + S[1,2]*m[1,2] + S[2,1]*m[2,1] +
S[1,3]*m[1,3] + S[3,1]*m[3,1] + S[1,4]*m[1,4] + S[4,1]*m[4,1] + S[1,5]*m[1,5] +
S[5,1]*m[5,1] + S[1,6]*m[1,6] + S[6,1]*m[6,1] + S[1,7]*m[1,7] + S[7,1]*m[7,1] +
S[1,8]*m[1,8] + S[8,1]*m[8,1] + S[1,9]*m[1,9] + S[9,1]*m[9,1]
С2 01 =S[2,1]*m[2,1] + S[1,2]*m[1,2]
+ S[2,2]*m[2,2] + S[2,2]*m[2,2] + S[2,3]*m[2,3] + S[3,2]*m[3,2] +
S[2,4]*m[4,2] + S[4,2]*m[4,2] + S[2,5]*m[2,5] + S[5,2]*m[5,2] + S[2,6]*m[2,6] +
S[6,2]*m[6,2] + S[2,7]*m[2,7] + S[7,2]*m[7,2] + S[2,8]*m[2,8] + S[8,2]*m[8,2] +
S[2,9]*m[2,9]+ S[9,2]*m[9,2]
С3 01=S[3,1]*m[3,1]
+ S[1,3]*m[1,3] + S[3,2]*m[3,2] + S[2,3]*m[2,3] + S[3,3]*m[3,3] +
S[3,3]*m[3,3] + S[3,4]*m[3,4] + S[4,3]*m[4,3] + S[3,5]*m[3,5] +
S[5,3]*m[5,3] + S[3,6]*m[3,6] + S[6,3]*m[6,3] + S[3,7]*m[3,7] + S[7,3]*m[7,3] +
S[3,8]*m[3,8] + S[8,3]*m[8,3] + S[3,9]*m[3,9] + S[9,3]*m[9,3]
С4 01
=S[4,1]*m[4,1] + S[1,4]*m[1,4] + S[4,2]*m[4,2] + S[2,4]*m[2,4] + S[4,3]*m[4,3]
+ S[3,4]*m[3,4] + S[4,4]*m[1,1] + S[4,4]*m[1,1] + S[4,5]*m[4,5] +
S[5,4]*m[5,4] + S[4,6]*m[4,6] + S[6,4]*m[6,4] + S[4,7]*m[4,7] +
S[7,4]*m[7,4] + S[4,8]*m[4,8] + S[8,4]*m[8,4] + S[4,9]*m[4,9]+ S[9,4]*m[9,4]
С5 01
=S[5,1]*m[5,1] + S[1,5]*m[1,5] + S[5,2]*m[5,2] + S[2,5]*m[2,5] + S[5,3]*m[5,3]
+ S[3,5]*m[3,5] + S[5,4]*m[5,4] + S[4,5]*m[4,5] + S[5,5]*m[5,5] +
S[5,5]*m[5,5] + S[5,6]*m[5,6] + S[6,5]*m[6,5] + S[5,7]*m[5,7] +
S[7,5]*m[7,5] + S[5,8]*m[5,8] + S[8,5]*m[8,5] + S[5,9]*m[5,9] + S[9,5]*m[9,5]
С6 01
=S[6,1]*m[6,1] + S[1,6]*m[1,6] + S[6,2]*m[6,2] + S[2,6]*m[2,6] + S[6,3]*m[6,3]
+ S[3,6]*m[3,6] + S[6,4]*m[6,4] + S[4,6]*m[4,6] + S[6,5]*m[6,5] + S[5,6]*m[5,6]
+ S[6,6]*m[6,6] + S[6,6]*m[6,6] + S[6,7]*m[6,7] + S[7,6]*m[7,6] +
S[6,8]*m[6,8] + S[8,6]*m[8,6] + S[6,9]*m[6,9] + S[9,6]*m[9,6]
С7 01
=S[7,1]*m[7,1] + S[1,7]*m[1,7] + S[7,2]*m[7,2] + S[2,7]*m[2,7] + S[7,3]*m[7,3]
+ S[3,7]*m[3,7] + S[7,4]*m[7,4] + S[4,7]*m[4,7] + S[7,5]*m[7,5] + S[5,7]*m[5,7]
+ S[7,6]*m[7,6] + S[6,7]*m[6,7] + S[7,7]*m[7,7] + S[7,7]*m[7,7] +
S[7,8]*m[7,8] + S[8,7]*m[8,7] + S[7,9]*m[7,9]+ S[9,7]*m[9,7]
С8 01
=S[8,1]*m[8,1] + S[1,8]*m[1,8] + S[8,2]*m[8,2] + S[2,8]*m[2,8] + S[8,3]*m[8,3]
+ S[3,8]*m[3,8] + S[8,4]*m[8,4] + S[4,8]*m[4,8] + S[8,5]*m[8,5] + S[5,8]*m[5,8]
+ S[8,6]*m[8,6] + S[6,8]*m[6,8] + S[8,7]*m[8,7] + S[7,8]*m[7,8] +
S[8,8]*m[8,8] + S[8,8]*m[8,8] + S[8,9]*m[8,9] + S[9,8]*m[9,8]
С9 01
=S[9,1]*m[9,1] + S[1,9]*m[1,9] + S[9,2]*m[9,2] + S[2,9]*m[2,9] + S[9,3]*m[9,3]
+ S[3,9]*m[3,9] + S[9,4]*m[9,4] + S[4,9]*m[4,9] + S[9,5]*m[9,5] + S[5,9]*m[5,9]
+ S[9,6]*m[9,6] + S[6,9]*m[6,9] + S[9,7]*m[9,7] + S[7,9]*m[7,9] + S[9,8]*m[9,8]
+ S[8,9]*m[8,9] + S[9,9]*m[9,9] + S[9,9]*m[9,9]
С 01 ={30, 60, 80, 100, 130, 104,
60 , 116, 80 }
П. 4 алгоритма
С11 Пω =
S[1,1]*m[1,1] + S[1,1]*m[1,1] + S[1,2]*m[1,2] + S[2,1]*m[2,1] +
S[1,3]*m[1,3] + S[3,1]*m[3,1] + S[1,4]*m[1,4] + S[4,1]*m[4,1] + S[1,5]*m[1,5] +
S[5,1]*m[5,1] + S[1,6]*m[1,6] + S[6,1]*m[6,1] + S[1,7]*m[1,7] + S[7,1]*m[7,1] +
S[1,8]*m[1,8] + S[8,1]*m[8,1] + S[1,9]*m[1,9] + S[9,1]*m[9,1] + S[1,1]*m[1,1] +
S[1,1]*m[1,1]
С12 Пω =
S[1,1]*m[2,1] + S[1,1]*m[1,2] + S[1,2]*m[2,2] + S[2,1]*m[2,2] + S[1,3]*m[2,3] +
S[3,1]*m[3,2] + S[1,4]*m[2,4] + S[4,1]*m[4,2] + S[1,5]*m[2,5] + S[5,1]*m[5,2] +
S[1,6]*m[2,6] + S[6,1]*m[6,2] + S[1,7]*m[2,7] + S[7,1]*m[7,2] + S[1,8]*m[2,8] +
S[8,1]*m[8,2] + S[1,9]*m[2,9] + S[9,1]*m[9,2] + S[1,2]*m[1,2] + S[2,1]*m[2,1]
C13 Пω = S[1,1]*m[3,1] + S[1,1]*m[1,3] + S[1,2]*m[3,2]
+ S[2,1]*m[2,3] + S[1,3]*m[3,3] + S[3,1]*m[3,3] + S[1,4]*m[3,4] +
S[4,1]*m[4,3] + S[1,5]*m[3,5] + S[5,1]*m[5,3] + S[1,6]*m[3,6] + S[6,1]*m[6,3] +
S[1,7]*m[3,7] + S[7,1]*m[7,3] + S[1,8]*m[3,8] + S[8,1]*m[8,3] + S[1,9]*m[3,9] +
S[9,1]*m[9,3] + S[1,3]*m[1,3] + S[3,1]*m[3,1]
С14 Пω =
S[1,1]*m[4,1] + S[1,1]*m[1,4] + S[1,2]*m[4,2] + S[2,1]*m[2,4] +
S[1,3]*m[4,3] + S[3,1]*m[3,4] + S[1,4]*m[4,4] + S[4,1]*m[4,4] + S[1,5]*m[4,5] +
S[5,1]*m[5,4] + S[1,6]*m[4,6] + S[6,1]*m[6,4] + S[1,7]*m[4,7] + S[7,1]*m[7,4] +
S[1,8]*m[4,8] + S[8,1]*m[8,4] + S[1,9]*m[4,9] + S[9,1]*m[9,4] + S[1,4]*m[1,4] +
S[4,1]*m[4,1]
С15 Пω =
S[1,1]*m[5,1] + S[1,1]*m[1,5] + S[1,2]*m[5,2] + S[2,1]*m[2,5] +
S[1,3]*m[5,3] + S[3,1]*m[3,5] + S[1,4]*m[5,4] + S[4,1]*m[4,5] + S[1,5]*m[5,5] +
S[5,1]*m[5,5] + S[1,6]*m[5,6] + S[6,1]*m[6,5] + S[1,7]*m[5,7] + S[7,1]*m[7,5] +
S[1,8]*m[5,8] + S[8,1]*m[8,5] + S[1,9]*m[5,9] + S[9,1]*m[9,5] + S[1,5]*m[1,5] +
S[5,1]*m[5,1]
С16 Пω =
S[1,1]*m[6,1] + S[1,1]*m[1,6] + S[1,2]*m[6,2] + S[2,1]*m[2,6] +
S[1,3]*m[6,3] + S[3,1]*m[3,6] + S[1,4]*m[6,4] + S[4,1]*m[4,6] + S[1,5]*m[6,5] +
S[5,1]*m[5,6] + S[1,6]*m[6,6] + S[6,1]*m[6,6] + S[1,7]*m[6,7] + S[7,1]*m[7,6] +
S[1,8]*m[6,8] + S[8,1]*m[8,6] + S[1,9]*m[6,9] + S[9,1]*m[9,6] + S[1,6]*m[1,6] +
S[6,1]*m[6,1]
С17 Пω =
S[1,1]*m[7,1] + S[1,1]*m[1,7] + S[1,2]*m[7,2] + S[2,1]*m[2,7] +
S[1,3]*m[7,3] + S[3,1]*m[3,7] + S[1,4]*m[7,4] + S[4,1]*m[4,7] + S[1,5]*m[7,5] +
S[5,1]*m[5,7] + S[1,6]*m[7,6] + S[6,1]*m[6,7] + S[1,7]*m[7,7] + S[7,1]*m[7,7] +
S[1,8]*m[7,8] + S[8,1]*m[8,7] + S[1,9]*m[7,9] + S[9,1]*m[9,7] + S[1,7]*m[1,7] +
S[7,1]*m[7,1]
С18 Пω =
S[1,1]*m[8,1] + S[1,1]*m[1,8] + S[1,2]*m[8,2] + S[2,1]*m[2,8] +
S[1,3]*m[8,3] + S[3,1]*m[3,8] + S[1,4]*m[8,4] + S[4,1]*m[4,8] + S[1,5]*m[8,5] +
S[5,1]*m[5,8] + S[1,6]*m[8,6] + S[6,1]*m[6,8] + S[1,7]*m[8,7] + S[7,1]*m[7,8] +
S[1,8]*m[8,8] + S[8,1]*m[8,8] + S[1,9]*m[8,9] + S[9,1]*m[9,8] + S[1,8]*m[1,8] +
S[8,1]*m[8,1]
С19 Пω
[1,9]= S[1,1]*m[9,1] + S[1,1]*m[1,9] + S[1,2]*m[9,2] + S[2,1]*m[2,9]
+ S[1,3]*m[9,3] + S[3,1]*m[3,9] + S[1,4]*m[9,4] + S[4,1]*m[4,9] + S[1,5]*m[9,5]
+ S[5,1]*m[5,9] + S[1,6]*m[9,6] + S[6,1]*m[6,9] + S[1,7]*m[9,7] + S[7,1]*m[7,9]
+ S[1,8]*m[9,8] + S[8,1]*m[8,9] + S[1,9]*m[9,9] + S[9,1]*m[9,9] + S[1,9]*m[1,9]
+ S[9,1]*m[9,1]
С21 Пω =
S[2,1]*m[1,1] + S[1,2]*m[1,1] + S[2,2]*m[1,2] + S[2,2]*m[2,1] + S[2,3]*m[1,3]
+ S[3,2]*m[3,1] + S[2,4]*m[1,4] + S[4,2]*m[4,1] + S[2,5]*m[1,5] +
S[5,2]*m[5,1] + S[2,6]*m[1,6] + S[6,2]*m[6,1] + S[2,7]*m[1,7] + S[7,2]*m[7,1] +
S[2,8]*m[1,8] + S[8,2]*m[8,1] + S[2,9]*m[1,9] + S[9,2]*m[9,1] + S[2,1]*m[2,1]
+ S[1,2]*m[1,2]
………………………………………………………………
С99 Пω =
S[9,1]*m[9,1] + S[1,9]*m[1,9] + S[9,2]*m[9,2] + S[2,9]*m[2,9] + S[9,3]*m[9,3] +
S[3,9]*m[3,9] + S[9,4]*m[9,4] + S[4,9]*m[4,9] + S[9,5]*m[9,5] + S[5,9]*m[5,9] +
S[9,6]*m[9,6] + S[6,9]*m[6,9] + S[9,7]*m[9,7] + S[7,9]*m[7,9] + S[9,8]*m[9,8]
+ S[8,9]*m[8,9] + S[9,9]*m[9,9] + S[9,9]*m[9,9] + S[9,9]*m[9,9] +
S[9,9]*m[9,9]
Получили
матрицу С Пω :
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
30 |
30 |
30 |
22 |
70 |
110 |
100 |
96 |
180 |
|
2 |
78 |
60 |
78 |
100 |
200 |
280 |
300 |
240 |
400 |
|
3 |
80 |
52 |
80 |
72 |
120 |
200 |
180 |
166 |
300 |
|
4 |
148 |
100 |
150 |
100 |
150 |
220 |
210 |
172 |
340 |
|
5 |
190 |
132 |
192 |
140 |
130 |
170 |
104 |
130 |
200 |
|
6 |
250 |
170 |
250 |
130 |
140 |
104 |
84 |
88 |
196 |
|
7 |
260 |
206 |
260 |
160 |
132 |
84 |
60 |
96 |
160 |
|
8 |
350 |
280 |
350 |
200 |
200 |
104 |
92 |
116 |
136 |
|
9 |
120 |
96 |
120 |
70 |
52 |
60 |
36 |
80 |
80 |
Рисунок 6
Найдём
элементы матрицы Qω по выражению (4):
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
0 |
18 |
0 |
40 |
100 |
226 |
270 |
300 |
196 |
|
2 |
18 |
0 |
-10 |
40 |
142 |
286 |
386 |
344 |
356 |
|
3 |
0 |
-10 |
0 |
42 |
100 |
266 |
300 |
320 |
260 |
|
4 |
40 |
40 |
42 |
0 |
60 |
146 |
210 |
156 |
230 |
|
5 |
100 |
142 |
100 |
60 |
0 |
76 |
46 |
84 |
42 |
|
6 |
226 |
286 |
266 |
146 |
76 |
0 |
4 |
-28 |
72 |
|
7 |
270 |
386 |
300 |
210 |
46 |
4 |
0 |
12 |
56 |
|
8 |
300 |
344 |
320 |
156 |
84 |
-28 |
12 |
0 |
20 |
|
9 |
196 |
356 |
260 |
230 |
42 |
72 |
56 |
20 |
0 |
Рисунок 7
Получили: min Q= -28
<0
p:=y6=6 , v:=y8=8 è y6:=v=8 , y8:=p=6 и переход к п.3 (т.е. к
Итерации 2)
(т.е.
у нас y = { 1, 2, 3, 4, 5, 8, 7, 6,
9})
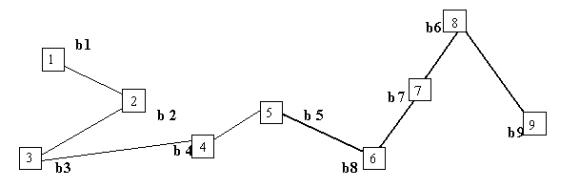
Рисунок 8
Итерация 2:
С1 01 =
S[1,1]*m[1,1] + S[1,1]*m[1,1] + S[1,2]*m[1,2] + S[2,1]*m[2,1] +
S[1,3]*m[1,3] + S[3,1]*m[3,1] + S[1,4]*m[1,4] + S[4,1]*m[4,1] + S[1,5]*m[1,5] +
S[5,1]*m[5,1] + S[1,6]*m[1,8] + S[6,1]*m[8,1] + S[1,7]*m[1,7] + S[7,1]*m[7,1] +
S[1,8]*m[1,6] + S[8,1]*m[6,1] + S[1,9]*m[1,9] + S[9,1]*m[9,1]
С2 01 = S[2,1]*m[2,1] + S[1,2]*m[1,2]
+ S[2,2]*m[2,2] + S[2,2]*m[2,2] + S[2,3]*m[2,3] + S[3,2]*m[3,2] +
S[2,4]*m[2,4] + S[4,2]*m[4,2] + S[2,5]*m[2,5] + S[5,2]*m[5,2] + S[2,6]*m[2,8] +
S[6,2]*m[8,2] + S[2,7]*m[2,7] + S[7,2]*m[7,2] + S[2,8]*m[2,6] + S[8,2]*m[6,2] +
S[2,9]*m[2,9] + S[9,2]*m[9,2]
С3 01=
S[3,1]*m[3,1] + S[1,3]*m[1,3] + S[3,2]*m[3,2] + S[2,3]*m[2,3] +
S[3,3]*m[3,3] + S[3,3]*m[3,3] + S[3,4]*m[3,4] + S[4,3]*m[4,3] +
S[3,5]*m[3,5] + S[5,3]*m[5,3] + S[3,6]*m[3,8] + S[6,3]*m[8,3] + S[3,7]*m[3,7] +
S[7,3]*m[7,3] + S[3,8]*m[3,6] + S[8,3]*m[6,3] + S[3,9]*m[3,9] + S[9,3]*m[9,3]
С4 01 =
S[4,1]*m[4,1] + S[1,4]*m[1,4] + S[4,2]*m[4,2] + S[2,4]*m[2,4] + S[4,3]*m[4,3]
+ S[3,4]*m[3,4] + S[4,4]*m[4,4] + S[4,4]*m[4,4] + S[4,5]*m[4,5] +
S[5,4]*m[5,4] + S[4,6]*m[4,8] + S[6,4]*m[8,4] + S[4,7]*m[4,7] +
S[7,4]*m[7,4] + S[4,8]*m[4,6] + S[8,4]*m[6,4] + S[4,9]*m[4,9] + S[9,4]*m[9,4]
С5 01 =
S[5,1]*m[5,1] + S[1,5]*m[1,5] + S[5,2]*m[5,2] + S[2,5]*m[2,5] + S[5,3]*m[5,3] +
S[3,5]*m[3,5] + S[5,4]*m[5,4] + S[4,5]*m[4,5] + S[5,5]*m[5,5] +
S[5,5]*m[5,5] + S[5,6]*m[5,8] + S[6,5]*m[8,5] + S[5,7]*m[5,7] +
S[7,5]*m[7,5] + S[5,8]*m[5,6] + S[8,5]*m[6,5] + S[5,9]*m[5,9] + S[9,5]*m[9,5]
С6 01 =
S[6,1]*m[8,1] + S[1,6]*m[1,8] + S[6,2]*m[8,2] + S[2,6]*m[2,8] + S[6,3]*m[8,3] +
S[3,6]*m[3,8] + S[6,4]*m[8,4] + S[4,6]*m[4,8] + S[6,5]*m[8,5] + S[5,6]*m[5,8]
+ S[6,6]*m[8,8] + S[6,6]*m[8,8] + S[6,7]*m[8,7] + S[7,6]*m[7,8] +
S[6,8]*m[8,6] + S[8,6]*m[6,8] + S[6,9]*m[8,9] + S[9,6]*m[9,8]
С7 01 =
S[7,1]*m[7,1] + S[1,7]*m[1,7] + S[7,2]*m[7,2] + S[2,7]*m[2,7] + S[7,3]*m[7,3] +
S[3,7]*m[3,7] + S[7,4]*m[7,4] + S[4,7]*m[4,7] + S[7,5]*m[7,5] + S[5,7]*m[5,7] +
S[7,6]*m[7,8] + S[6,7]*m[8,7] + S[7,7]*m[7,7] + S[7,7]*m[7,7] + S[7,8]*m[7,6]
+ S[8,7]*m[6,7] + S[7,9]*m[7,9] + S[9,7]*m[9,7]
С8 01 =
S[8,1]*m[6,1] + S[1,8]*m[1,6] + S[8,2]*m[6,2] + S[2,8]*m[2,6] + S[8,3]*m[6,3] +
S[3,8]*m[3,6] + S[8,4]*m[6,4] + S[4,8]*m[4,6] + S[8,5]*m[6,5] + S[5,8]*m[5,6] +
S[8,6]*m[6,8] + S[6,8]*m[8,6] + S[8,7]*m[6,7] + S[7,8]*m[7,6] +
S[8,8]*m[6,6] + S[8,8]*m[6,6] + S[8,9]*m[6,9] + S[9,8]*m[9,6]
С9 01 =
S[9,1]*m[9,1] + S[1,9]*m[1,9] + S[9,2]*m[9,2] + S[2,9]*m[2,9] + S[9,3]*m[9,3] +
S[3,9]*m[3,9] + S[9,4]*m[9,4] + S[4,9]*m[4,9] + S[9,5]*m[9,5] + S[5,9]*m[5,9] +
S[9,6]*m[9,8] + S[6,9]*m[8,9] + S[9,7]*m[9,7] + S[7,9]*m[7,9] + S[9,8]*m[9,6]
+ S[8,9]*m[6,9] + S[9,9]*m[9,9] + S[9,9]*m[9,9]
С 01 ={30, 60, 80, 100, 102, 88,
60 , 104, 80 }
С11 Пω =
S[1,1]*m[1,1] + S[1,1]*m[1,1] + S[1,2]*m[1,2] + S[2,1]*m[2,1] +
S[1,3]*m[1,3] + S[3,1]*m[3,1] + S[1,4]*m[1,4] + S[4,1]*m[4,1] + S[1,5]*m[1,5] +
S[5,1]*m[5,1] + S[1,6]*m[1,8] + S[6,1]*m[8,1] + S[1,7]*m[1,7] + S[7,1]*m[7,1] +
S[1,8]*m[1,6] + S[8,1]*m[6,1] + S[1,9]*m[1,9] + S[9,1]*m[9,1] + S[1,1]*m[1,1] +
S[1,1]*m[1,1]
С12 Пω =
S[1,1]*m[2,1] + S[1,1]*m[1,2] + S[1,2]*m[2,2] + S[2,1]*m[2,2] + S[1,3]*m[2,3] +
S[3,1]*m[3,2] + S[1,4]*m[2,4] + S[4,1]*m[4,2] + S[1,5]*m[2,5] + S[5,1]*m[5,2] +
S[1,6]*m[2,8] + S[6,1]*m[8,2] + S[1,7]*m[2,7] + S[7,1]*m[7,2] + S[1,8]*m[2,6] +
S[8,1]*m[6,2] + S[1,9]*m[2,9] + S[9,1]*m[9,2] + S[1,2]*m[1,2] + S[2,1]*m[2,1]
C13 Пω = S[1,1]*m[3,1] + S[1,1]*m[1,3] + S[1,2]*m[3,2]
+ S[2,1]*m[2,3] + S[1,3]*m[3,3] + S[3,1]*m[3,3] + S[1,4]*m[3,4] +
S[4,1]*m[4,3] + S[1,5]*m[3,5] + S[5,1]*m[5,3] + S[1,6]*m[3,8] + S[6,1]*m[8,3] +
S[1,7]*m[3,7] + S[7,1]*m[7,3] + S[1,8]*m[3,6] + S[8,1]*m[6,3] + S[1,9]*m[3,9] +
S[9,1]*m[9,3] + S[1,3]*m[1,3] + S[3,1]*m[3,1]
С14 Пω =
S[1,1]*m[4,1] + S[1,1]*m[1,4] + S[1,2]*m[4,2] + S[2,1]*m[2,4] +
S[1,3]*m[4,3] + S[3,1]*m[3,4] + S[1,4]*m[4,4] + S[4,1]*m[4,4] + S[1,5]*m[4,5] +
S[5,1]*m[5,4] + S[1,6]*m[4,8] + S[6,1]*m[8,4] + S[1,7]*m[4,7] + S[7,1]*m[7,4] +
S[1,8]*m[4,6] + S[8,1]*m[6,4] + S[1,9]*m[4,9] + S[9,1]*m[9,4] + S[1,4]*m[1,4] +
S[4,1]*m[4,1]
С15 Пω =
S[1,1]*m[5,1] + S[1,1]*m[1,5] + S[1,2]*m[5,2] + S[2,1]*m[2,5] +
S[1,3]*m[5,3] + S[3,1]*m[3,5] + S[1,4]*m[5,4] + S[4,1]*m[4,5] + S[1,5]*m[5,5] +
S[5,1]*m[5,5] + S[1,6]*m[5,8] + S[6,1]*m[8,5] + S[1,7]*m[5,7] + S[7,1]*m[7,5] +
S[1,8]*m[5,6] + S[8,1]*m[6,5] + S[1,9]*m[5,9] + S[9,1]*m[9,5] + S[1,5]*m[1,5] +
S[5,1]*m[5,1]
С16 Пω =
S[1,1]*m[8,1] + S[1,1]*m[1,8] + S[1,2]*m[8,2] + S[2,1]*m[2,8] +
S[1,3]*m[8,3] + S[3,1]*m[3,8] + S[1,4]*m[8,4] + S[4,1]*m[4,8] + S[1,5]*m[8,5] +
S[5,1]*m[5,8] + S[1,6]*m[8,8] + S[6,1]*m[8,8] + S[1,7]*m[8,7] + S[7,1]*m[7,8] +
S[1,8]*m[8,6] + S[8,1]*m[6,8] + S[1,9]*m[8,9] + S[9,1]*m[9,8] + S[1,6]*m[1,8] +
S[6,1]*m[8,1]
С17 Пω =
S[1,1]*m[7,1] + S[1,1]*m[1,7] + S[1,2]*m[7,2] + S[2,1]*m[2,7] +
S[1,3]*m[7,3] + S[3,1]*m[3,7] + S[1,4]*m[7,4] + S[4,1]*m[4,7] + S[1,5]*m[7,5] +
S[5,1]*m[5,7] + S[1,6]*m[7,8] + S[6,1]*m[8,7] + S[1,7]*m[7,7] + S[7,1]*m[7,7] +
S[1,8]*m[7,6] + S[8,1]*m[6,7] + S[1,9]*m[7,9] + S[9,1]*m[9,7] + S[1,7]*m[1,7] +
S[7,1]*m[7,1]
С18 Пω =
S[1,1]*m[6,1] + S[1,1]*m[1,6] + S[1,2]*m[6,2] + S[2,1]*m[2,6] +
S[1,3]*m[6,3] + S[3,1]*m[3,6] + S[1,4]*m[6,4] + S[4,1]*m[4,6] + S[1,5]*m[6,5] +
S[5,1]*m[5,6] + S[1,6]*m[6,8] + S[6,1]*m[8,6] + S[1,7]*m[6,7] + S[7,1]*m[7,6] +
S[1,8]*m[6,6] + S[8,1]*m[6,6] + S[1,9]*m[6,9] + S[9,1]*m[9,6] + S[1,8]*m[1,6] +
S[8,1]*m[6,1]
С19 Пω
[1,9]= S[1,1]*m[9,1] + S[1,1]*m[1,9] + S[1,2]*m[9,2] + S[2,1]*m[2,9]
+ S[1,3]*m[9,3] + S[3,1]*m[3,9] + S[1,4]*m[9,4] + S[4,1]*m[4,9] + S[1,5]*m[9,5]
+ S[5,1]*m[5,9] + S[1,6]*m[9,8] + S[6,1]*m[8,9] + S[1,7]*m[9,7] + S[7,1]*m[7,9]
+ S[1,8]*m[9,6] + S[8,1]*m[6,9] + S[1,9]*m[9,9] + S[9,1]*m[9,9] + S[1,9]*m[1,9]
+ S[9,1]*m[9,1]
С21 Пω =
S[2,1]*m[1,1] + S[1,2]*m[1,1] + S[2,2]*m[1,2] + S[2,2]*m[2,1] + S[2,3]*m[1,3]
+ S[3,2]*m[3,1] + S[2,4]*m[1,4] + S[4,2]*m[4,1] + S[2,5]*m[1,5] +
S[5,2]*m[5,1] + S[2,6]*m[1,8] + S[6,2]*m[8,1] + S[2,7]*m[1,7] + S[7,2]*m[7,1] +
S[2,8]*m[1,6] + S[8,2]*m[6,1] + S[2,9]*m[1,9] + S[9,2]*m[9,1] + S[2,1]*m[2,1]
+ S[1,2]*m[1,2]
………………………………………………………………
С99 Пω =
S[9,1]*m[9,1] + S[1,9]*m[1,9] + S[9,2]*m[9,2] + S[2,9]*m[2,9] + S[9,3]*m[9,3] +
S[3,9]*m[3,9] + S[9,4]*m[9,4] + S[4,9]*m[4,9] + S[9,5]*m[9,5] + S[5,9]*m[5,9] +
S[9,6]*m[9,8] + S[6,9]*m[8,9] + S[9,7]*m[9,7] + S[7,9]*m[7,9] + S[9,8]*m[9,6]
+ S[8,9]*m[6,9] + S[9,9]*m[9,9] + S[9,9]*m[9,9] + S[9,9]*m[9,9] +
S[9,9]*m[9,9]
Получили
матрицу С Пω :
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
30 |
30 |
30 |
22 |
70 |
96 |
100 |
110 |
180 |
|
2 |
78 |
60 |
78 |
100 |
200 |
240 |
300 |
280 |
400 |
|
3 |
80 |
52 |
80 |
72 |
120 |
166 |
180 |
200 |
300 |
|
4 |
148 |
100 |
150 |
100 |
150 |
172 |
210 |
220 |
340 |
|
5 |
170 |
118 |
170 |
120 |
102 |
122 |
116 |
150 |
200 |
|
6 |
250 |
170 |
250 |
130 |
112 |
88 |
96 |
104 |
196 |
|
7 |
260 |
206 |
260 |
160 |
132 |
96 |
60 |
84 |
160 |
|
8 |
350 |
280 |
350 |
200 |
200 |
116 |
80 |
104 |
136 |
|
9 |
140 |
110 |
140 |
90 |
80 |
60 |
24 |
80 |
80 |
Рисунок 9
Найдём
элементы матрицы Qω по выражению (4):
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
0 |
18 |
0 |
40 |
108 |
228 |
270 |
326 |
210 |
|
2 |
18 |
0 |
-10 |
40 |
156 |
262 |
386 |
396 |
370 |
|
3 |
0 |
-10 |
0 |
42 |
108 |
248 |
300 |
366 |
280 |
|
4 |
40 |
40 |
42 |
0 |
68 |
114 |
210 |
216 |
250 |
|
5 |
108 |
156 |
108 |
68 |
0 |
44 |
86 |
144 |
98 |
|
6 |
228 |
262 |
248 |
114 |
44 |
0 |
44 |
28 |
88 |
|
7 |
270 |
386 |
300 |
210 |
86 |
44 |
0 |
0 |
44 |
|
8 |
326 |
396 |
366 |
216 |
144 |
28 |
0 |
0 |
32 |
|
9 |
210 |
370 |
280 |
250 |
98 |
88 |
44 |
32 |
0 |
Рисунок 10
Получили: min Q= -10
<0
p:=y2=2 , v:=y3=3 è y2:=v=3 , y3:=p=2 и переход к п.3 (т.е. к
Итерации 2)
(т.е.
у нас y = { 1, 3, 2, 4, 5, 8, 7, 6,
9})
Рисунок 11
Итерация 3:
С1 01 =
S[1,1]*m[1,1] + S[1,1]*m[1,1] + S[1,2]*m[1,3] + S[2,1]*m[3,1] +
S[1,3]*m[1,2] + S[3,1]*m[2,1] + S[1,4]*m[1,4] + S[4,1]*m[4,1] + S[1,5]*m[1,5] +
S[5,1]*m[5,1] + S[1,6]*m[1,8] + S[6,1]*m[8,1] + S[1,7]*m[1,7] + S[7,1]*m[7,1] +
S[1,8]*m[1,6] + S[8,1]*m[6,1] + S[1,9]*m[1,9] + S[9,1]*m[9,1]
С2 01 = S[2,1]*m[3,1] + S[1,2]*m[1,3]
+ S[2,2]*m[3,3] + S[2,2]*m[3,3] + S[2,3]*m[3,2] + S[3,2]*m[2,3] +
S[2,4]*m[3,4] + S[4,2]*m[4,3] + S[2,5]*m[3,5] + S[5,2]*m[5,3] + S[2,6]*m[3,8] +
S[6,2]*m[8,3] + S[2,7]*m[3,7] + S[7,2]*m[7,3] + S[2,8]*m[3,6] + S[8,2]*m[6,3] +
S[2,9]*m[3,9] + S[9,2]*m[9,3]
С3 01=
S[3,1]*m[2,1] + S[1,3]*m[1,2] + S[3,2]*m[2,3] + S[2,3]*m[3,2] +
S[3,3]*m[2,2] + S[3,3]*m[2,2] + S[3,4]*m[2,4] + S[4,3]*m[4,2] +
S[3,5]*m[2,5] + S[5,3]*m[5,2] + S[3,6]*m[2,8] + S[6,3]*m[8,2] + S[3,7]*m[2,7] +
S[7,3]*m[7,2] + S[3,8]*m[2,6] + S[8,3]*m[6,2] + S[3,9]*m[2,9] + S[9,3]*m[9,2]
С4 01 =
S[4,1]*m[4,1] + S[1,4]*m[1,4] + S[4,2]*m[4,3] + S[2,4]*m[3,4] + S[4,3]*m[4,2]
+ S[3,4]*m[2,4] + S[4,4]*m[4,4] + S[4,4]*m[4,4] + S[4,5]*m[4,5] +
S[5,4]*m[5,4] + S[4,6]*m[4,8] + S[6,4]*m[8,4] + S[4,7]*m[4,7] +
S[7,4]*m[7,4] + S[4,8]*m[4,6] + S[8,4]*m[6,4] + S[4,9]*m[4,9] + S[9,4]*m[9,4]
С5 01 =
S[5,1]*m[5,1] + S[1,5]*m[1,5] + S[5,2]*m[5,3] + S[2,5]*m[3,5] + S[5,3]*m[5,2] +
S[3,5]*m[2,5] + S[5,4]*m[5,4] + S[4,5]*m[4,5] + S[5,5]*m[5,5] +
S[5,5]*m[5,5] + S[5,6]*m[5,8] + S[6,5]*m[8,5] + S[5,7]*m[5,7] +
S[7,5]*m[7,5] + S[5,8]*m[5,6] + S[8,5]*m[6,5] + S[5,9]*m[5,9] + S[9,5]*m[9,5]
С6 01 =
S[6,1]*m[8,1] + S[1,6]*m[1,8] + S[6,2]*m[8,3] + S[2,6]*m[3,8] + S[6,3]*m[8,2] +
S[3,6]*m[2,8] + S[6,4]*m[8,4] + S[4,6]*m[4,8] + S[6,5]*m[8,5] + S[5,6]*m[5,8]
+ S[6,6]*m[8,8] + S[6,6]*m[8,8] + S[6,7]*m[8,7] + S[7,6]*m[7,8] +
S[6,8]*m[8,6] + S[8,6]*m[6,8] + S[6,9]*m[8,9] + S[9,6]*m[9,8]
С7 01 =
S[7,1]*m[7,1] + S[1,7]*m[1,7] + S[7,2]*m[7,3] + S[2,7]*m[3,7] + S[7,3]*m[7,2] +
S[3,7]*m[2,7] + S[7,4]*m[7,4] + S[4,7]*m[4,7] + S[7,5]*m[7,5] + S[5,7]*m[5,7] +
S[7,6]*m[7,8] + S[6,7]*m[8,7] + S[7,7]*m[7,7] + S[7,7]*m[7,7] + S[7,8]*m[7,6]
+ S[8,7]*m[6,7] + S[7,9]*m[7,9] + S[9,7]*m[9,7]
С8 01 =
S[8,1]*m[6,1] + S[1,8]*m[1,6] + S[8,2]*m[6,3] + S[2,8]*m[3,6] + S[8,3]*m[6,2] +
S[3,8]*m[2,6] + S[8,4]*m[6,4] + S[4,8]*m[4,6] + S[8,5]*m[6,5] + S[5,8]*m[5,6] +
S[8,6]*m[6,8] + S[6,8]*m[8,6] + S[8,7]*m[6,7] + S[7,8]*m[7,6] +
S[8,8]*m[6,6] + S[8,8]*m[6,6] + S[8,9]*m[6,9] + S[9,8]*m[9,6]
С9 01 =
S[9,1]*m[9,1] + S[1,9]*m[1,9] + S[9,2]*m[9,3] + S[2,9]*m[3,9] + S[9,3]*m[9,2] +
S[3,9]*m[2,9] + S[9,4]*m[9,4] + S[4,9]*m[4,9] + S[9,5]*m[9,5] + S[5,9]*m[5,9] +
S[9,6]*m[9,8] + S[6,9]*m[8,9] + S[9,7]*m[9,7] + S[7,9]*m[7,9] + S[9,8]*m[9,6]
+ S[8,9]*m[6,9] + S[9,9]*m[9,9] + S[9,9]*m[9,9]
С 01 ={48, 78, 52, 72, 102, 88, 60 , 104, 80 }
С11 Пω =
S[1,1]*m[1,1] + S[1,1]*m[1,1] + S[1,2]*m[1,3] + S[2,1]*m[3,1] +
S[1,3]*m[1,2] + S[3,1]*m[2,1] + S[1,4]*m[1,4] + S[4,1]*m[4,1] + S[1,5]*m[1,5] +
S[5,1]*m[5,1] + S[1,6]*m[1,8] + S[6,1]*m[8,1] + S[1,7]*m[1,7] + S[7,1]*m[7,1] +
S[1,8]*m[1,6] + S[8,1]*m[6,1] + S[1,9]*m[1,9] + S[9,1]*m[9,1] + S[1,1]*m[1,1] +
S[1,1]*m[1,1]
С12 Пω =
S[1,1]*m[3,1] + S[1,1]*m[1,3] + S[1,2]*m[3,3] + S[2,1]*m[3,3] + S[1,3]*m[3,2] +
S[3,1]*m[2,3] + S[1,4]*m[3,4] + S[4,1]*m[4,3] + S[1,5]*m[3,5] + S[5,1]*m[5,3] +
S[1,6]*m[3,8] + S[6,1]*m[8,3] + S[1,7]*m[3,7] + S[7,1]*m[7,3] + S[1,8]*m[3,6] +
S[8,1]*m[6,3] + S[1,9]*m[3,9] + S[9,1]*m[9,3] + S[1,2]*m[1,3] + S[2,1]*m[3,1]
C13 Пω = S[1,1]*m[2,1] + S[1,1]*m[1,2] + S[1,2]*m[2,3]
+ S[2,1]*m[3,2] + S[1,3]*m[2,2] + S[3,1]*m[2,2] + S[1,4]*m[2,4] +
S[4,1]*m[4,2] + S[1,5]*m[2,5] + S[5,1]*m[5,2] + S[1,6]*m[2,8] + S[6,1]*m[8,2] +
S[1,7]*m[2,7] + S[7,1]*m[7,2] + S[1,8]*m[2,6] + S[8,1]*m[6,2] + S[1,9]*m[2,9] +
S[9,1]*m[9,2] + S[1,3]*m[1,2] + S[3,1]*m[2,1]
С14 Пω =
S[1,1]*m[4,1] + S[1,1]*m[1,4] + S[1,2]*m[4,3] + S[2,1]*m[3,4] +
S[1,3]*m[4,2] + S[3,1]*m[2,4] + S[1,4]*m[4,4] + S[4,1]*m[4,4] + S[1,5]*m[4,5] +
S[5,1]*m[5,4] + S[1,6]*m[4,8] + S[6,1]*m[8,4] + S[1,7]*m[4,7] + S[7,1]*m[7,4] +
S[1,8]*m[4,6] + S[8,1]*m[6,4] + S[1,9]*m[4,9] + S[9,1]*m[9,4] + S[1,4]*m[1,4] +
S[4,1]*m[4,1]
С15 Пω =
S[1,1]*m[5,1] + S[1,1]*m[1,5] + S[1,2]*m[5,3] + S[2,1]*m[3,5] +
S[1,3]*m[5,2] + S[3,1]*m[2,5] + S[1,4]*m[5,4] + S[4,1]*m[4,5] + S[1,5]*m[5,5] +
S[5,1]*m[5,5] + S[1,6]*m[5,8] + S[6,1]*m[8,5] + S[1,7]*m[5,7] + S[7,1]*m[7,5] +
S[1,8]*m[5,6] + S[8,1]*m[6,5] + S[1,9]*m[5,9] + S[9,1]*m[9,5] + S[1,5]*m[1,5] +
S[5,1]*m[5,1]
С16 Пω =
S[1,1]*m[8,1] + S[1,1]*m[1,8] + S[1,2]*m[8,3] + S[2,1]*m[3,8] +
S[1,3]*m[8,2] + S[3,1]*m[2,8] + S[1,4]*m[8,4] + S[4,1]*m[4,8] + S[1,5]*m[8,5] +
S[5,1]*m[5,8] + S[1,6]*m[8,8] + S[6,1]*m[8,8] + S[1,7]*m[8,7] + S[7,1]*m[7,8] +
S[1,8]*m[8,6] + S[8,1]*m[6,8] + S[1,9]*m[8,9] + S[9,1]*m[9,8] + S[1,6]*m[1,8] +
S[6,1]*m[8,1]
С17 Пω =
S[1,1]*m[7,1] + S[1,1]*m[1,7] + S[1,2]*m[7,3] + S[2,1]*m[3,7] +
S[1,3]*m[7,2] + S[3,1]*m[2,7] + S[1,4]*m[7,4] + S[4,1]*m[4,7] + S[1,5]*m[7,5] +
S[5,1]*m[5,7] + S[1,6]*m[7,8] + S[6,1]*m[8,7] + S[1,7]*m[7,7] + S[7,1]*m[7,7] +
S[1,8]*m[7,6] + S[8,1]*m[6,7] + S[1,9]*m[7,9] + S[9,1]*m[9,7] + S[1,7]*m[1,7] +
S[7,1]*m[7,1]
С18 Пω =
S[1,1]*m[6,1] + S[1,1]*m[1,6] + S[1,2]*m[6,3] + S[2,1]*m[3,6] +
S[1,3]*m[6,2] + S[3,1]*m[2,6] + S[1,4]*m[6,4] + S[4,1]*m[4,6] + S[1,5]*m[6,5] +
S[5,1]*m[5,6] + S[1,6]*m[6,8] + S[6,1]*m[8,6] + S[1,7]*m[6,7] + S[7,1]*m[7,6] +
S[1,8]*m[6,6] + S[8,1]*m[6,6] + S[1,9]*m[6,9] + S[9,1]*m[9,6] + S[1,8]*m[1,6] +
S[8,1]*m[6,1]
С19 Пω
[1,9]= S[1,1]*m[9,1] + S[1,1]*m[1,9] + S[1,2]*m[9,3] + S[2,1]*m[3,9]
+ S[1,3]*m[9,2] + S[3,1]*m[2,9] + S[1,4]*m[9,4] + S[4,1]*m[4,9] + S[1,5]*m[9,5]
+ S[5,1]*m[5,9] + S[1,6]*m[9,8] + S[6,1]*m[8,9] + S[1,7]*m[9,7] + S[7,1]*m[7,9]
+ S[1,8]*m[9,6] + S[8,1]*m[6,9] + S[1,9]*m[9,9] + S[9,1]*m[9,9] + S[1,9]*m[1,9]
+ S[9,1]*m[9,1]
С21 Пω =
S[2,1]*m[1,1] + S[1,2]*m[1,1] + S[2,2]*m[1,3] + S[2,2]*m[3,1] + S[2,3]*m[1,2]
+ S[3,2]*m[2,1] + S[2,4]*m[1,4] + S[4,2]*m[4,1] + S[2,5]*m[1,5] +
S[5,2]*m[5,1] + S[2,6]*m[1,8] + S[6,2]*m[8,1] + S[2,7]*m[1,7] + S[7,2]*m[7,1] +
S[2,8]*m[1,6] + S[8,2]*m[6,1] + S[2,9]*m[1,9] + S[9,2]*m[9,1] + S[2,1]*m[3,1]
+ S[1,2]*m[1,3]
………………………………………………………………
С99 Пω =
S[9,1]*m[9,1] + S[1,9]*m[1,9] + S[9,2]*m[9,3] + S[2,9]*m[3,9] + S[9,3]*m[9,2] +
S[3,9]*m[2,9] + S[9,4]*m[9,4] + S[4,9]*m[4,9] + S[9,5]*m[9,5] + S[5,9]*m[5,9] +
S[9,6]*m[9,8] + S[6,9]*m[8,9] + S[9,7]*m[9,7] + S[7,9]*m[7,9] + S[9,8]*m[9,6]
+ S[8,9]*m[6,9] + S[9,9]*m[9,9] + S[9,9]*m[9,9] + S[9,9]*m[9,9] +
S[9,9]*m[9,9]
Получили
матрицу С Пω :
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
48 |
48 |
30 |
50 |
100 |
120 |
150 |
140 |
200 |
|
2 |
78 |
78 |
60 |
72 |
170 |
216 |
250 |
250 |
380 |
|
3 |
98 |
80 |
52 |
72 |
150 |
190 |
230 |
230 |
320 |
|
4 |
130 |
130 |
92 |
72 |
120 |
148 |
160 |
190 |
320 |
|
5 |
170 |
170 |
118 |
120 |
102 |
122 |
116 |
150 |
200 |
|
6 |
250 |
250 |
170 |
130 |
112 |
88 |
96 |
104 |
196 |
|
7 |
260 |
260 |
206 |
160 |
132 |
96 |
60 |
84 |
160 |
|
8 |
350 |
350 |
280 |
200 |
200 |
116 |
80 |
104 |
136 |
|
9 |
140 |
140 |
110 |
90 |
80 |
60 |
24 |
80 |
80 |
Рисунок 12
Найдём
элементы матрицы Qω по выражению (4):
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
0 |
0 |
28 |
60 |
120 |
234 |
302 |
338 |
212 |
|
2 |
0 |
0 |
10 |
52 |
160 |
300 |
372 |
418 |
362 |
|
3 |
28 |
10 |
0 |
40 |
114 |
220 |
324 |
354 |
298 |
|
4 |
60 |
52 |
40 |
0 |
66 |
118 |
188 |
214 |
258 |
|
5 |
120 |
160 |
114 |
66 |
0 |
44 |
86 |
144 |
98 |
|
6 |
234 |
300 |
220 |
118 |
44 |
0 |
44 |
28 |
88 |
|
7 |
302 |
372 |
324 |
188 |
86 |
44 |
0 |
0 |
44 |
|
8 |
338 |
418 |
354 |
214 |
144 |
28 |
0 |
0 |
32 |
|
9 |
212 |
362 |
298 |
258 |
98 |
88 |
44 |
32 |
0 |
Рисунок 13
Получили: min Q= 0 ³ 0, следовательно переходим
к п. 12
П. 12 . Корректировка номера
исходного варианта
ω = ω +1 = 2;
П. 13
ω£N,
значит переходим к п. 2
П. 2 Формирование
для варианта ω исходного списка
{yi}ω
y = { 2, 3, 4, 5, 6, 7, 8, 9, 1}
Рисунок
14
П. 3
Итерация 1:
С1 02 =
S[1,1]*m[2,2] + S[1,1]*m[2,2] + S[1,2]*m[2,3] + S[2,1]*m[3,2] + S[1,3]*m[2,4]
+ S[3,1]*m[4,2] + S[1,4]*m[2,5] + S[4,1]*m[5,2] + S[1,5]*m[2,6] + S[5,1]*m[6,2]
+ S[1,6]*m[2,7] + S[6,1]*m[7,2] + S[1,7]*m[2,8] + S[7,1]*m[8,2] + S[1,8]*m[2,9]
+ S[8,1]*m[9,2] + S[1,9]*m[2,1] + S[9,1]*m[1,2]
С2 02 = S[2,1]*m[3,2] + S[1,2]*m[2,3]
+ S[2,2]*m[3,3] + S[2,2]*m[3,3] + S[2,3]*m[3,4] + S[3,2]*m[4,3] +
S[2,4]*m[3,5] + S[4,2]*m[5,3] + S[2,5]*m[3,6] + S[5,2]*m[6,3] + S[2,6]*m[3,7] +
S[6,2]*m[7,3] + S[2,7]*m[3,8] + S[7,2]*m[8,3] + S[2,8]*m[3,9] + S[8,2]*m[9,3] +
S[2,9]*m[3,1] + S[9,2]*m[1,3]
С3 02=
S[3,1]*m[4,2] + S[1,3]*m[2,4] + S[3,2]*m[4,3] + S[2,3]*m[3,4] +
S[3,3]*m[4,4] + S[3,3]*m[4,4] + S[3,4]*m[4,5] + S[4,3]*m[5,4] +
S[3,5]*m[4,6] + S[5,3]*m[6,4] + S[3,6]*m[4,7] + S[6,3]*m[7,4] + S[3,7]*m[4,8] +
S[7,3]*m[8,4] + S[3,8]*m[4,9] + S[8,3]*m[9,4] + S[3,9]*m[4,1] + S[9,3]*m[1,4]
С4 02 =
S[4,1]*m[5,2] + S[1,4]*m[2,5] + S[4,2]*m[5,3] + S[2,4]*m[3,5] + S[4,3]*m[5,4]
+ S[3,4]*m[4,5] + S[4,4]*m[5,5] + S[4,4]*m[5,5] + S[4,5]*m[5,6] +
S[5,4]*m[6,5] + S[4,6]*m[5,7] + S[6,4]*m[7,5] + S[4,7]*m[5,8] + S[7,4]*m[8,5]
+ S[4,8]*m[5,9] + S[8,4]*m[9,5] + S[4,9]*m[5,1] + S[9,4]*m[1,5]
С5 02 =
S[5,1]*m[6,2] + S[1,5]*m[2,6] + S[5,2]*m[6,3] + S[2,5]*m[3,6] + S[5,3]*m[6,4] +
S[3,5]*m[4,6] + S[5,4]*m[6,5] + S[4,5]*m[5,6] + S[5,5]*m[6,6] +
S[5,5]*m[6,6] + S[5,6]*m[6,7] + S[6,5]*m[7,6] + S[5,7]*m[6,8] +
S[7,5]*m[8,6] + S[5,8]*m[6,9] + S[8,5]*m[9,6] + S[5,9]*m[6,1] + S[9,5]*m[1,6]
С6 02 =
S[6,1]*m[7,2] + S[1,6]*m[2,7] + S[6,2]*m[7,3] + S[2,6]*m[3,7] + S[6,3]*m[7,4] +
S[3,6]*m[4,7] + S[6,4]*m[7,5] + S[4,6]*m[5,7] + S[6,5]*m[7,6] + S[5,6]*m[6,7]
+ S[6,6]*m[7,7] + S[6,6]*m[7,7] + S[6,7]*m[7,8] + S[7,6]*m[8,7] +
S[6,8]*m[7,9] + S[8,6]*m[9,7] + S[6,9]*m[7,1] + S[9,6]*m[1,7]
С7 02 =
S[7,1]*m[8,2] + S[1,7]*m[2,8] + S[7,2]*m[8,3] + S[2,7]*m[3,8] + S[7,3]*m[8,4] +
S[3,7]*m[4,8] + S[7,4]*m[8,5] + S[4,7]*m[5,8] + S[7,5]*m[8,6] + S[5,7]*m[6,8] +
S[7,6]*m[8,7] + S[6,7]*m[7,8] + S[7,7]*m[8,8] + S[7,7]*m[8,8] + S[7,8]*m[8,9]
+ S[8,7]*m[9,8] + S[7,9]*m[8,1] + S[9,7]*m[1,8]
С8 02 =
S[8,1]*m[9,2] + S[1,8]*m[2,9] + S[8,2]*m[9,3] + S[2,8]*m[3,9] + S[8,3]*m[9,4] +
S[3,8]*m[4,9] + S[8,4]*m[9,5] + S[4,8]*m[5,9] + S[8,5]*m[9,6] + S[5,8]*m[6,9] +
S[8,6]*m[9,7] + S[6,8]*m[7,9] + S[8,7]*m[9,8] + S[7,8]*m[8,9] +
S[8,8]*m[9,9] + S[8,8]*m[9,9] + S[8,9]*m[9,1] + S[9,8]*m[1,9]
С9 02 =
S[9,1]*m[1,2] + S[1,9]*m[2,1] + S[9,2]*m[1,3] + S[2,9]*m[3,1] + S[9,3]*m[1,4] +
S[3,9]*m[4,1] + S[9,4]*m[1,5] + S[4,9]*m[5,1] + S[9,5]*m[1,6] + S[5,9]*m[6,1] +
S[9,6]*m[1,7] + S[6,9]*m[7,1] + S[9,7]*m[1,8] + S[7,9]*m[8,1] + S[9,8]*m[1,9]
+ S[8,9]*m[9,1] + S[9,9]*m[1,1] + S[9,9]*m[1,1]
С 02 ={30, 80, 100, 130, 104, 60,
116, 280, 200}
П. 4
С11 Пω =
S[1,1]*m[2,2] + S[1,1]*m[2,2] + S[1,2]*m[2,3] + S[2,1]*m[3,2] +
S[1,3]*m[2,4] + S[3,1]*m[4,2] + S[1,4]*m[2,5] + S[4,1]*m[5,2] + S[1,5]*m[2,6] +
S[5,1]*m[6,2] + S[1,6]*m[2,7] + S[6,1]*m[7,2] + S[1,7]*m[2,8] + S[7,1]*m[8,2] +
S[1,8]*m[2,9] + S[8,1]*m[9,2] + S[1,9]*m[2,1] + S[9,1]*m[1,2] + S[1,1]*m[2,2] +
S[1,1]*m[2,2]
С12 Пω =
S[1,1]*m[3,2] + S[1,1]*m[2,3] + S[1,2]*m[3,3] + S[2,1]*m[3,3] + S[1,3]*m[3,4] +
S[3,1]*m[4,3] + S[1,4]*m[3,5] + S[4,1]*m[5,3] + S[1,5]*m[3,6] + S[5,1]*m[6,3] +
S[1,6]*m[3,7] + S[6,1]*m[7,3] + S[1,7]*m[3,8] + S[7,1]*m[8,3] + S[1,8]*m[3,9] +
S[8,1]*m[9,3] + S[1,9]*m[3,1] + S[9,1]*m[1,3] + S[1,2]*m[2,3] + S[2,1]*m[3,2]
C13 Пω = S[1,1]*m[4,2] + S[1,1]*m[2,4] + S[1,2]*m[4,3]
+ S[2,1]*m[3,4] + S[1,3]*m[4,4] + S[3,1]*m[4,4] + S[1,4]*m[4,5] +
S[4,1]*m[5,4] + S[1,5]*m[4,6] + S[5,1]*m[6,4] + S[1,6]*m[4,7] + S[6,1]*m[7,4] +
S[1,7]*m[4,8] + S[7,1]*m[8,4] + S[1,8]*m[4,9] + S[8,1]*m[9,4] + S[1,9]*m[4,1] +
S[9,1]*m[1,4] + S[1,3]*m[2,4] + S[3,1]*m[4,2]
С14 Пω =
S[1,1]*m[5,2] + S[1,1]*m[2,5] + S[1,2]*m[5,3] + S[2,1]*m[3,5] +
S[1,3]*m[5,4] + S[3,1]*m[4,5] + S[1,4]*m[5,5] + S[4,1]*m[5,5] + S[1,5]*m[5,6] +
S[5,1]*m[6,5] + S[1,6]*m[5,7] + S[6,1]*m[7,5] + S[1,7]*m[5,8] + S[7,1]*m[8,5] +
S[1,8]*m[5,9] + S[8,1]*m[9,5] + S[1,9]*m[5,1] + S[9,1]*m[1,5] + S[1,4]*m[2,5] +
S[4,1]*m[5,2]
С15 Пω =
S[1,1]*m[6,2] + S[1,1]*m[2,6] + S[1,2]*m[6,3] + S[2,1]*m[3,6] +
S[1,3]*m[6,4] + S[3,1]*m[4,6] + S[1,4]*m[6,5] + S[4,1]*m[5,6] + S[1,5]*m[6,6] +
S[5,1]*m[6,6] + S[1,6]*m[6,7] + S[6,1]*m[7,6] + S[1,7]*m[6,8] + S[7,1]*m[8,6] +
S[1,8]*m[6,9] + S[8,1]*m[9,6] + S[1,9]*m[6,1] + S[9,1]*m[1,6] + S[1,5]*m[2,6] +
S[5,1]*m[6,2]
С16 Пω =
S[1,1]*m[7,2] + S[1,1]*m[2,7] + S[1,2]*m[7,3] + S[2,1]*m[3,7] +
S[1,3]*m[7,4] + S[3,1]*m[4,7] + S[1,4]*m[7,5] + S[4,1]*m[5,7] + S[1,5]*m[7,6] +
S[5,1]*m[6,7] + S[1,6]*m[7,7] + S[6,1]*m[7,7] + S[1,7]*m[7,8] + S[7,1]*m[8,7] +
S[1,8]*m[7,9] + S[8,1]*m[9,7] + S[1,9]*m[7,1] + S[9,1]*m[1,7] + S[1,6]*m[2,7] +
S[6,1]*m[7,2]
С17 Пω =
S[1,1]*m[8,2] + S[1,1]*m[2,8] + S[1,2]*m[8,3] + S[2,1]*m[3,8] +
S[1,3]*m[8,4] + S[3,1]*m[4,8] + S[1,4]*m[8,5] + S[4,1]*m[5,8] + S[1,5]*m[8,6] +
S[5,1]*m[6,8] + S[1,6]*m[8,7] + S[6,1]*m[7,8] + S[1,7]*m[8,8] + S[7,1]*m[8,8] +
S[1,8]*m[8,9] + S[8,1]*m[9,8] + S[1,9]*m[8,1] + S[9,1]*m[1,8] + S[1,7]*m[2,8] +
S[7,1]*m[8,2]
С18 Пω =
S[1,1]*m[9,2] + S[1,1]*m[2,9] + S[1,2]*m[9,3] + S[2,1]*m[3,9] +
S[1,3]*m[9,4] + S[3,1]*m[4,9] + S[1,4]*m[9,5] + S[4,1]*m[5,9] + S[1,5]*m[9,6] +
S[5,1]*m[6,9] + S[1,6]*m[9,7] + S[6,1]*m[7,9] + S[1,7]*m[9,8] + S[7,1]*m[8,9] +
S[1,8]*m[9,9] + S[8,1]*m[9,9] + S[1,9]*m[9,1] + S[9,1]*m[1,9] + S[1,8]*m[2,9] +
S[8,1]*m[9,2]
С19 Пω
[1,9]= S[1,1]*m[1,2] + S[1,1]*m[2,1] + S[1,2]*m[1,3] + S[2,1]*m[3,1]
+ S[1,3]*m[1,4] + S[3,1]*m[4,1] + S[1,4]*m[1,5] + S[4,1]*m[5,1] + S[1,5]*m[1,6]
+ S[5,1]*m[6,1] + S[1,6]*m[1,7] + S[6,1]*m[7,1] + S[1,7]*m[1,8] + S[7,1]*m[8,1]
+ S[1,8]*m[1,9] + S[8,1]*m[9,1] + S[1,9]*m[1,1] + S[9,1]*m[1,1] + S[1,9]*m[2,1]
+ S[9,1]*m[1,2]
С21 Пω =
S[2,1]*m[2,2] + S[1,2]*m[2,2] + S[2,2]*m[2,3] + S[2,2]*m[3,2] + S[2,3]*m[2,4]
+ S[3,2]*m[4,2] + S[2,4]*m[2,5] + S[4,2]*m[5,2] + S[2,5]*m[2,6] +
S[5,2]*m[6,2] + S[2,6]*m[2,7] + S[6,2]*m[7,2] + S[2,7]*m[2,8] + S[7,2]*m[8,2] +
S[2,8]*m[2,9] + S[8,2]*m[9,2] + S[2,9]*m[2,1] + S[9,2]*m[1,2] + S[2,1]*m[3,2]
+ S[1,2]*m[2,3]
………………………………………………………………
С99 Пω = S[9,1]*m[1,2]
+ S[1,9]*m[2,1] + S[9,2]*m[1,3] + S[2,9]*m[3,1] + S[9,3]*m[1,4] + S[3,9]*m[4,1]
+ S[9,4]*m[1,5] + S[4,9]*m[5,1] + S[9,5]*m[1,6] + S[5,9]*m[6,1] + S[9,6]*m[1,7]
+ S[6,9]*m[7,1] + S[9,7]*m[1,8] + S[7,9]*m[8,1] + S[9,8]*m[1,9] + S[8,9]*m[9,1]
+ S[9,9]*m[1,1] + S[9,9]*m[1,1] + S[9,9]*m[1,1] + S[9,9]*m[1,1]
Получили
матрицу С Пω :
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
30 |
30 |
50 |
100 |
140 |
150 |
120 |
200 |
48 |
|
2 |
52 |
80 |
72 |
120 |
200 |
180 |
166 |
300 |
80 |
|
3 |
100 |
150 |
100 |
150 |
220 |
210 |
172 |
340 |
148 |
|
4 |
132 |
190 |
140 |
130 |
170 |
104 |
130 |
200 |
190 |
|
5 |
170 |
250 |
130 |
140 |
104 |
84 |
88 |
196 |
250 |
|
6 |
206 |
260 |
160 |
132 |
84 |
60 |
96 |
160 |
260 |
|
7 |
280 |
350 |
200 |
200 |
104 |
92 |
116 |
136 |
350 |
|
8 |
126 |
168 |
120 |
152 |
200 |
186 |
200 |
280 |
320 |
|
9 |
180 |
200 |
120 |
140 |
80 |
56 |
80 |
200 |
200 |
Рисунок 15
Найдём
элементы матрицы Qω по выражению (4):
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
0 |
-28 |
20 |
72 |
176 |
266 |
254 |
16 |
-2 |
|
2 |
-28 |
0 |
42 |
100 |
266 |
300 |
320 |
108 |
0 |
|
3 |
20 |
42 |
0 |
60 |
146 |
210 |
156 |
80 |
-32 |
|
4 |
72 |
100 |
60 |
0 |
76 |
46 |
84 |
-58 |
0 |
|
5 |
176 |
266 |
146 |
76 |
0 |
4 |
-28 |
12 |
26 |
|
6 |
266 |
300 |
210 |
46 |
4 |
0 |
12 |
6 |
56 |
|
7 |
254 |
320 |
156 |
84 |
-28 |
12 |
0 |
-60 |
114 |
|
8 |
16 |
108 |
80 |
-58 |
12 |
6 |
-60 |
0 |
40 |
|
9 |
-2 |
0 |
-32 |
0 |
26 |
56 |
114 |
40 |
0 |
Рисунок 16
Получили: min Q= -60
<0
p:=y7=8 , v:=y8=9 è y7:=v=9 , y8:=p=8 и переход к п.3 (т.е. к
Итерации 2)
(т.е.
у нас y = { 2, 3, 4, 5, 6, 7, 9, 8,
1})
Рисунок 17
Итерация 2:
С1 02 =
S[1,1]*m[2,2] + S[1,1]*m[2,2] + S[1,2]*m[2,3] + S[2,1]*m[3,2] +
S[1,3]*m[2,4] + S[3,1]*m[4,2] + S[1,4]*m[2,5] + S[4,1]*m[5,2] + S[1,5]*m[2,6] +
S[5,1]*m[6,2] + S[1,6]*m[2,7] + S[6,1]*m[7,2] + S[1,7]*m[2,9] + S[7,1]*m[9,2] +
S[1,8]*m[2,8] + S[8,1]*m[8,2] + S[1,9]*m[2,1] + S[9,1]*m[1,2]
С2 02 = S[2,1]*m[3,2] + S[1,2]*m[2,3]
+ S[2,2]*m[3,3] + S[2,2]*m[3,3] + S[2,3]*m[3,4] + S[3,2]*m[4,3] +
S[2,4]*m[3,5] + S[4,2]*m[5,3] + S[2,5]*m[3,6] + S[5,2]*m[6,3] + S[2,6]*m[3,7] +
S[6,2]*m[7,3] + S[2,7]*m[3,9] + S[7,2]*m[9,3] + S[2,8]*m[3,8] + S[8,2]*m[8,3] +
S[2,9]*m[3,1] + S[9,2]*m[1,3]
С3 02=
S[3,1]*m[4,2] + S[1,3]*m[2,4] + S[3,2]*m[4,3] + S[2,3]*m[3,4] +
S[3,3]*m[4,4] + S[3,3]*m[4,4] + S[3,4]*m[4,5] + S[4,3]*m[5,4] +
S[3,5]*m[4,6] + S[5,3]*m[6,4] + S[3,6]*m[4,7] + S[6,3]*m[7,4] + S[3,7]*m[4,9] +
S[7,3]*m[9,4] + S[3,8]*m[4,8] + S[8,3]*m[8,4] + S[3,9]*m[4,1] + S[9,3]*m[1,4]
С4 02 =
S[4,1]*m[5,2] + S[1,4]*m[2,5] + S[4,2]*m[5,3] + S[2,4]*m[3,5] + S[4,3]*m[5,4]
+ S[3,4]*m[4,5] + S[4,4]*m[5,5] + S[4,4]*m[5,5] + S[4,5]*m[5,6] +
S[5,4]*m[6,5] + S[4,6]*m[5,7] + S[6,4]*m[7,5] + S[4,7]*m[5,9] + S[7,4]*m[9,5]
+ S[4,8]*m[5,8] + S[8,4]*m[8,5] + S[4,9]*m[5,1] + S[9,4]*m[1,5]
С5 02 =
S[5,1]*m[6,2] + S[1,5]*m[2,6] + S[5,2]*m[6,3] + S[2,5]*m[3,6] + S[5,3]*m[6,4] +
S[3,5]*m[4,6] + S[5,4]*m[6,5] + и + S[5,5]*m[6,6] +
S[5,5]*m[6,6] + S[5,6]*m[6,7] + S[6,5]*m[7,6] + S[5,7]*m[6,9] +
S[7,5]*m[9,6] + S[5,8]*m[6,8] + S[8,5]*m[8,6] + S[5,9]*m[6,1] + S[9,5]*m[1,6]
С6 02 =
S[6,1]*m[7,2] + S[1,6]*m[2,7] + S[6,2]*m[7,3] + S[2,6]*m[3,7] + S[6,3]*m[7,4] +
S[3,6]*m[4,7] + S[6,4]*m[7,5] + S[4,6]*m[5,7] + S[6,5]*m[7,6] + S[5,6]*m[6,7]
+ S[6,6]*m[7,7] + S[6,6]*m[7,7] + S[6,7]*m[7,9] + S[7,6]*m[9,7] +
S[6,8]*m[7,8] + S[8,6]*m[8,7] + S[6,9]*m[7,1] + S[9,6]*m[1,7]
С7 02 =
S[7,1]*m[9,2] + S[1,7]*m[2,9] + S[7,2]*m[9,3] + S[2,7]*m[3,9] + S[7,3]*m[9,4] +
S[3,7]*m[4,9] + S[7,4]*m[9,5] + S[4,7]*m[5,9] + S[7,5]*m[9,6] + S[5,7]*m[6,9] +
S[7,6]*m[9,7] + S[6,7]*m[7,9] + S[7,7]*m[9,9] + S[7,7]*m[9,9] + S[7,8]*m[9,8]
+ S[8,7]*m[8,9] + S[7,9]*m[9,1] + S[9,7]*m[1,9]
С8 02 =
S[8,1]*m[8,2] + S[1,8]*m[2,8] + S[8,2]*m[8,3] + S[2,8]*m[3,8] + S[8,3]*m[8,4] +
S[3,8]*m[4,8] + S[8,4]*m[8,5] + S[4,8]*m[5,8] + S[8,5]*m[8,6] + S[5,8]*m[6,8] +
S[8,6]*m[8,7] + S[6,8]*m[7,8] + S[8,7]*m[8,9] + S[7,8]*m[9,8] +
S[8,8]*m[8,8] + S[8,8]*m[8,8] + S[8,9]*m[8,1] + S[9,8]*m[1,8]
С9 02 =
S[9,1]*m[1,2] + S[1,9]*m[2,1] + S[9,2]*m[1,3] + S[2,9]*m[3,1] + S[9,3]*m[1,4] +
S[3,9]*m[4,1] + S[9,4]*m[1,5] + S[4,9]*m[5,1] + S[9,5]*m[1,6] + S[5,9]*m[6,1] +
S[9,6]*m[1,7] + S[6,9]*m[7,1] + S[9,7]*m[1,9] + S[7,9]*m[9,1] + S[9,8]*m[1,8]
+ S[8,9]*m[8,1] + S[9,9]*m[1,1] + S[9,9]*m[1,1]
С 02 ={ 30, 80, 100, 130, 104, 80, 136, 200, 120}
П. 4
С11 Пω =
S[1,1]*m[2,2] + S[1,1]*m[2,2] + S[1,2]*m[2,3] + S[2,1]*m[3,2] +
S[1,3]*m[2,4] + S[3,1]*m[4,2] + S[1,4]*m[2,5] + S[4,1]*m[5,2] + S[1,5]*m[2,6] +
S[5,1]*m[6,2] + S[1,6]*m[2,7] + S[6,1]*m[7,2] + S[1,7]*m[2,9] + S[7,1]*m[9,2] +
S[1,8]*m[2,8] + S[8,1]*m[8,2] + S[1,9]*m[2,1] + S[9,1]*m[1,2] + S[1,1]*m[2,2] +
S[1,1]*m[2,2]
С12 Пω =
S[1,1]*m[3,2] + S[1,1]*m[2,3] + S[1,2]*m[3,3] + S[2,1]*m[3,3] + S[1,3]*m[3,4] +
S[3,1]*m[4,3] + S[1,4]*m[3,5] + S[4,1]*m[5,3] + S[1,5]*m[3,6] + S[5,1]*m[6,3] +
S[1,6]*m[3,7] + S[6,1]*m[7,3] + S[1,7]*m[3,9] + S[7,1]*m[9,3] + S[1,8]*m[3,8] +
S[8,1]*m[8,3] + S[1,9]*m[3,1] + S[9,1]*m[1,3] + S[1,2]*m[2,3] + S[2,1]*m[3,2]
C13 Пω = S[1,1]*m[4,2] + S[1,1]*m[2,4] + S[1,2]*m[4,3]
+ S[2,1]*m[3,4] + S[1,3]*m[4,4] + S[3,1]*m[4,4] + S[1,4]*m[4,5] +
S[4,1]*m[5,4] + S[1,5]*m[4,6] + S[5,1]*m[6,4] + S[1,6]*m[4,7] + S[6,1]*m[7,4] +
S[1,7]*m[4,9] + S[7,1]*m[9,4] + S[1,8]*m[4,8] + S[8,1]*m[8,4] + S[1,9]*m[4,1] +
S[9,1]*m[1,4] + S[1,3]*m[2,4] + S[3,1]*m[4,2]
С14 Пω =
S[1,1]*m[5,2] + S[1,1]*m[2,5] + S[1,2]*m[5,3] + S[2,1]*m[3,5] +
S[1,3]*m[5,4] + S[3,1]*m[4,5] + S[1,4]*m[5,5] + S[4,1]*m[5,5] + S[1,5]*m[5,6] +
S[5,1]*m[6,5] + S[1,6]*m[5,7] + S[6,1]*m[7,5] + S[1,7]*m[5,9] + S[7,1]*m[9,5] +
S[1,8]*m[5,8] + S[8,1]*m[8,5] + S[1,9]*m[5,1] + S[9,1]*m[1,5] + S[1,4]*m[2,5] +
S[4,1]*m[5,2]
С15 Пω =
S[1,1]*m[6,2] + S[1,1]*m[2,6] + S[1,2]*m[6,3] + S[2,1]*m[3,6] +
S[1,3]*m[6,4] + S[3,1]*m[4,6] + S[1,4]*m[6,5] + S[4,1]*m[5,6] + S[1,5]*m[6,6] +
S[5,1]*m[6,6] + S[1,6]*m[6,7] + S[6,1]*m[7,6] + S[1,7]*m[6,9] + S[7,1]*m[9,6] +
S[1,8]*m[6,8] + S[8,1]*m[8,6] + S[1,9]*m[6,1] + S[9,1]*m[1,6] + S[1,5]*m[2,6] +
S[5,1]*m[6,2]
С16 Пω =
S[1,1]*m[7,2] + S[1,1]*m[2,7] + S[1,2]*m[7,3] + S[2,1]*m[3,7] +
S[1,3]*m[7,4] + S[3,1]*m[4,7] + S[1,4]*m[7,5] + S[4,1]*m[5,7] + S[1,5]*m[7,6] +
S[5,1]*m[6,7] + S[1,6]*m[7,7] + S[6,1]*m[7,7] + S[1,7]*m[7,9] + S[7,1]*m[9,7] +
S[1,8]*m[7,8] + S[8,1]*m[8,7] + S[1,9]*m[7,1] + S[9,1]*m[1,7] + S[1,6]*m[2,7] +
S[6,1]*m[7,2]
С17 Пω =
S[1,1]*m[9,2] + S[1,1]*m[2,9] + S[1,2]*m[9,3] + S[2,1]*m[3,9] +
S[1,3]*m[9,4] + S[3,1]*m[4,9] + S[1,4]*m[9,5] + S[4,1]*m[5,9] + S[1,5]*m[9,6] +
S[5,1]*m[6,9] + S[1,6]*m[9,7] + S[6,1]*m[7,9] + S[1,7]*m[9,9] + S[7,1]*m[9,9] +
S[1,8]*m[9,8] + S[8,1]*m[8,9] + S[1,9]*m[9,1] + S[9,1]*m[1,9] + S[1,7]*m[2,9] +
S[7,1]*m[9,2]
С18 Пω =
S[1,1]*m[8,2] + S[1,1]*m[2,8] + S[1,2]*m[8,3] + S[2,1]*m[3,8] +
S[1,3]*m[8,4] + S[3,1]*m[4,8] + S[1,4]*m[8,5] + S[4,1]*m[5,8] + S[1,5]*m[8,6] +
S[5,1]*m[6,8] + S[1,6]*m[8,7] + S[6,1]*m[7,8] + S[1,7]*m[8,9] + S[7,1]*m[9,8] +
S[1,8]*m[8,8] + S[8,1]*m[8,8] + S[1,9]*m[8,1] + S[9,1]*m[1,8] + S[1,8]*m[2,8] +
S[8,1]*m[8,2]
С19 Пω
S[1,1]*m[1,2] + S[1,1]*m[2,1] + S[1,2]*m[1,3] + S[2,1]*m[3,1] +
S[1,3]*m[1,4] + S[3,1]*m[4,1] + S[1,4]*m[1,5] + S[4,1]*m[5,1] + S[1,5]*m[1,6] +
S[5,1]*m[6,1] + S[1,6]*m[1,7] + S[6,1]*m[7,1] + S[1,7]*m[1,9] + S[7,1]*m[9,1] +
S[1,8]*m[1,8] + S[8,1]*m[8,1] + S[1,9]*m[1,1] + S[9,1]*m[1,1] + S[1,9]*m[2,1] +
S[9,1]*m[1,2]
С21 Пω =
S[2,1]*m[2,2] + S[1,2]*m[2,2] + S[2,2]*m[2,3] + S[2,2]*m[3,2] + S[2,3]*m[2,4]
+ S[3,2]*m[4,2] + S[2,4]*m[2,5] + S[4,2]*m[5,2] + S[2,5]*m[2,6] +
S[5,2]*m[6,2] + S[2,6]*m[2,7] + S[6,2]*m[7,2] + S[2,7]*m[2,9] + S[7,2]*m[9,2] +
S[2,8]*m[2,8] + S[8,2]*m[8,2] + S[2,9]*m[2,1] + S[9,2]*m[1,2] + S[2,1]*m[3,2]
+ S[1,2]*m[2,3]
………………………………………………………………
С99 Пω =
S[9,1]*m[1,2] + S[1,9]*m[2,1] + S[9,2]*m[1,3] + S[2,9]*m[3,1] + S[9,3]*m[1,4] +
S[3,9]*m[4,1] + S[9,4]*m[1,5] + S[4,9]*m[5,1] + S[9,5]*m[1,6] + S[5,9]*m[6,1] +
S[9,6]*m[1,7] + S[6,9]*m[7,1] + S[9,7]*m[1,9] + S[7,9]*m[9,1] + S[9,8]*m[1,8]
+ S[8,9]*m[8,1] + S[9,9]*m[1,1] + S[9,9]*m[1,1] + S[9,9]*m[1,1] +
S[9,9]*m[1,1]
Получили
матрицу С Пω :
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
30 |
30 |
50 |
100 |
140 |
150 |
200 |
120 |
48 |
|
2 |
52 |
80 |
72 |
120 |
200 |
180 |
300 |
166 |
80 |
|
3 |
100 |
150 |
100 |
150 |
220 |
210 |
340 |
172 |
148 |
|
4 |
132 |
190 |
140 |
130 |
170 |
104 |
200 |
130 |
190 |
|
5 |
170 |
250 |
130 |
140 |
104 |
84 |
196 |
88 |
250 |
|
6 |
290 |
340 |
210 |
220 |
104 |
80 |
136 |
140 |
340 |
|
7 |
196 |
270 |
150 |
112 |
84 |
92 |
136 |
116 |
270 |
|
8 |
210 |
248 |
170 |
240 |
220 |
206 |
280 |
200 |
320 |
|
9 |
96 |
120 |
70 |
52 |
60 |
36 |
80 |
120 |
120 |
Рисунок 18
дём
элементы матрицы Qω по выражению (4):
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
0 |
-28 |
20 |
72 |
176 |
330 |
230 |
100 |
-6 |
|
2 |
-28 |
0 |
42 |
100 |
266 |
360 |
354 |
134 |
0 |
|
3 |
20 |
42 |
0 |
60 |
146 |
240 |
254 |
42 |
-2 |
|
4 |
72 |
100 |
60 |
0 |
76 |
114 |
46 |
40 |
-8 |
|
5 |
176 |
266 |
146 |
76 |
0 |
4 |
40 |
4 |
86 |
|
6 |
330 |
360 |
240 |
114 |
4 |
0 |
12 |
66 |
176 |
|
7 |
230 |
354 |
254 |
46 |
40 |
12 |
0 |
60 |
94 |
|
8 |
100 |
134 |
42 |
40 |
4 |
66 |
60 |
0 |
120 |
|
9 |
-6 |
0 |
-2 |
-8 |
86 |
176 |
94 |
120 |
0 |
Рисунок 19
Получили: min Q= -28
<0
p:=y1=2 , v:=y2=3 è y1:=v=3 , y2:=p=2 и переход к п.3 (т.е. к
Итерации 3)
(т.е.
у нас y = { 3, 2, 4, 5, 6, 7, 9, 8,
1})
Рисунок 20
Все промежуточные результаты, иллюстрирующие
основные промежуточные значения для всех итераций и вариантов ω=1…9 (по
алгоритму), приведены в таблице рисунка 21.
|
Вариант v |
Итер ация |
Y1 |
Y2 |
Y3 |
Y4 |
Y5 |
Y6 |
Y7 |
Y8 |
Y9 |
Min Q |
Q0 |
|
1 |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
-28 |
|
|
2 |
1 |
2 |
3 |
4 |
5 |
8 |
7 |
6 |
9 |
-10 |
|
|
|
3 |
1 |
3 |
2 |
4 |
5 |
8 |
7 |
6 |
9 |
0 |
342 |
|
|
2 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
-60 |
|
|
2 |
2 |
3 |
4 |
5 |
6 |
7 |
9 |
8 |
1 |
-28 |
|
|
|
3 |
3 |
2 |
4 |
5 |
6 |
7 |
9 |
8 |
1 |
-8 |
|
|
|
4 |
3 |
2 |
4 |
1 |
6 |
7 |
9 |
8 |
5 |
-42 |
|
|
|
5 |
3 |
2 |
1 |
4 |
6 |
7 |
9 |
8 |
5 |
-10 |
|
|
|
6 |
3 |
1 |
2 |
4 |
6 |
7 |
9 |
8 |
5 |
0 |
402 |
|
|
3 |
1 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
-60 |
|
|
2 |
3 |
4 |
5 |
6 |
7 |
9 |
8 |
1 |
2 |
-24 |
|
|
|
3 |
3 |
4 |
5 |
6 |
7 |
9 |
8 |
2 |
1 |
-6 |
|
|
|
4 |
3 |
2 |
5 |
6 |
7 |
9 |
8 |
4 |
1 |
-6 |
|
|
|
5 |
3 |
2 |
4 |
6 |
7 |
9 |
8 |
5 |
1 |
0 |
454 |
|
|
4 |
1 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
-70 |
|
|
2 |
9 |
5 |
6 |
7 |
8 |
4 |
1 |
2 |
3 |
-76 |
|
|
|
3 |
9 |
8 |
6 |
7 |
5 |
4 |
1 |
2 |
3 |
-32 |
|
|
|
4 |
9 |
7 |
6 |
8 |
5 |
4 |
1 |
2 |
3 |
-10 |
|
|
|
5 |
9 |
7 |
6 |
8 |
5 |
4 |
2 |
1 |
3 |
0 |
342 |
|
|
5 |
1 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
-128 |
|
|
2 |
9 |
6 |
7 |
8 |
5 |
1 |
2 |
3 |
4 |
-60 |
|
|
|
3 |
9 |
6 |
7 |
8 |
5 |
4 |
2 |
3 |
1 |
0 |
342 |
|
|
6 |
1 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
-60 |
|
|
2 |
6 |
7 |
9 |
8 |
1 |
2 |
3 |
4 |
5 |
-28 |
|
|
|
3 |
6 |
7 |
9 |
8 |
5 |
2 |
3 |
4 |
1 |
-40 |
|
|
|
4 |
6 |
7 |
9 |
8 |
5 |
4 |
3 |
2 |
1 |
-20 |
|
|
|
5 |
9 |
7 |
6 |
8 |
5 |
4 |
3 |
2 |
1 |
-10 |
|
|
|
6 |
9 |
7 |
6 |
8 |
5 |
4 |
2 |
3 |
1 |
0 |
342 |
|
|
7 |
1 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
-60 |
|
|
2 |
7 |
9 |
8 |
1 |
2 |
3 |
4 |
5 |
6 |
-44 |
|
|
|
3 |
9 |
7 |
8 |
1 |
2 |
3 |
4 |
5 |
6 |
-20 |
|
|
|
4 |
9 |
7 |
6 |
1 |
2 |
3 |
4 |
5 |
8 |
-12 |
|
|
|
5 |
9 |
7 |
6 |
2 |
1 |
3 |
4 |
5 |
8 |
0 |
420 |
|
|
8 |
1 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
-80 |
|
|
2 |
9 |
8 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
-20 |
|
|
|
3 |
9 |
8 |
1 |
2 |
3 |
4 |
5 |
7 |
6 |
-10 |
|
|
|
4 |
9 |
8 |
4 |
2 |
3 |
1 |
5 |
7 |
6 |
-2 |
|
|
|
5 |
9 |
8 |
4 |
1 |
3 |
2 |
5 |
7 |
6 |
0 |
432 |
|
|
9 |
1 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
-60 |
|
|
2 |
8 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
9 |
-20 |
|
|
|
3 |
5 |
1 |
2 |
3 |
4 |
8 |
6 |
7 |
9 |
-18 |
|
|
|
4 |
4 |
1 |
2 |
3 |
5 |
8 |
6 |
7 |
9 |
-60 |
|
|
|
5 |
3 |
1 |
2 |
4 |
5 |
8 |
6 |
7 |
9 |
0 |
342 |
Рисунок 21
П. 14. Вывод результатов расчёта оптимального
значения целевой функции Q0 и списка оптимальных
решений {yi}*:
Получили несколько вариантов с одинаковыми значениями целевых функций
Q0 = 342
![]() {9, 7,
6, 8, 5, 4, 2, 1, 3} (вариант 4 )
{9, 7,
6, 8, 5, 4, 2, 1, 3} (вариант 4 )
{9, 6, 7, 8, 5, 4, 2, 3, 1} (вариант 5 )
{yi}* = {9, 7, 6,
8, 5, 4, 2, 3, 1} (вариант 6 )
{1, 3, 2, 4, 5, 8, 7, 6, 9} (вариант 1 )
{3, 1, 2, 4, 5, 8, 6, 7, 9} (вариант 9 )
Принимаем в качестве решения вариант 1