УСЛОВИЯ РЕАЛИЗУЕМОСТИ РЕГУЛЯРНЫХ ВЫЧИСЛИТЕЛЬНЫХ СХЕМ

Г.А. Калинина, Ю.Е. Мороховец

(Москва, Московский Энергетический Институт (ТУ), Россия)

В докладе рассмотрена модель распределенных регулярных вычислений, основанная на взаимодействии параллельно протекающих последовательных процессов [1], сформулированы и доказаны условия реализуемости произвольных регулярных схем.

Регулярные вычисления, как частный случай распределенных асинхронных вычислений, задаются посредством схем специального вида. Регулярная вычислительная схема (РВС) – абстракция понятия распределенного алгоритма, перерабатывающего исходные данные в результат в соответствии с регулярным, не от чего независящим логическим законом. В настоящее время регулярные схемы применяются для задания процессов обработки данных в кластерных системах и локальных вычислительных сетях. Примерами задач, решаемых посредствам РВС, являются задачи вычислительного характера (сортировка массивов, преобразование матриц, вычисление рядов и т.д.), экономические задачи и задачи управления.

РВС можно представить как конечное множество пронумерованных программ, для каждой из которых специфицирована структура данных и последовательность команд, преобразующих данные указанной структуры.

Ядро набора команд, используемых в программах РВС, содержит шесть видов команд: ввода данных INPUT, вывода данных OUTPUT, преобразования данных TRANSFORM, посылки сообщения SEND, приема сообщения RESEIVE, завершения программы HALT. Виды команд с указанием всех параметров подробно представлены в [2], например, команда ввода данных INPUT имеет вид áI,i,dpñ, где I – код операции ввода, i – номер источника данных, dp – указатель блока данных, входящего в структуру данных программы. Другие команды имеют аналогичную структуру.

Для иллюстрации применения РВС приведем пример умножения матриц C = A*B размерностью 4´4. Будем считать, что матрица A является константой вычислительной схемы, а матрица B вводится по столбцам (с указанием номера вводимого столбца) в процессе счета. Матрица-результат C выводится по строкам с указанием номера выводимой строки.

Рассмотрим два варианта организации вычислений, в которых РВС, реализующие вычисления, состоят из четырех взаимодействующих программ, имеющих одинаковые структуры данных [2], но различные последовательности команд, обусловленные использованием разных точек ввода и различным порядком ввода исходных данных (столбцов матрицы B), вывода результатов счета (строк матрицы C) и их порядком.

В качестве первого варианта рассмотрим РВС с распределенным двухточечным вводом/выводом и циркулярной передачей столбцов матрицы-множителя между программами (рисунок 1). Будем считать, что:

- ввод/вывод выполняется первой и третьей программами; каждая из этих программ вводит два столбца матрицы B с их номерами;

- первая (третья) программа сначала вводит, обрабатывает и передает всем другим программам столбцы матрицы B с их номерами, а затем уже принимает от третьей (первой) программы и обрабатывают столбцы матрицы B и их номера, введенные этой программой;

- вторая (четвертая) программа передает сформированную строку матрицы C и ее номер первой (третьей) программе для вывода; первая (третья) программа выводит сначала первую (третью), а затем – вторую (четвертую) строку матрицы C.

k=m=1	k=m=2	k=m=3	k=m=4
1. I, 1, 2	1. R, 1, 3, 2	1. I, 2, 2	1. R, 1, 5, 2
2. T, 1, 0	2. T, 1, 0	2. T, 1, 0	2. T, 1, 0
3. S, 2, 1, 2	3. R, 1, 8, 2	3. S, 1, 11, 2	3. R, 1, 10, 2
4. S, 3, 11, 2	4. T, 1, 0	4. S, 2, 5, 2	4. T, 1, 0
5. S, 4, 1, 2	5. R, 3, 4, 2	5. S, 4, 5, 2	5. R, 3, 5, 2
6. I, 1, 2	6. T, 1, 0	6. I, 2, 2	6. T, 1, 0
7. T, 1, 0	7. R, 3, 9, 2	7. T, 1, 0	7. R, 3, 10, 2
8. S, 2, 3, 2	8. T, 1, 0	8. S, 1, 13, 2	8. T, 1, 0
9. S, 3, 13, 2	9. S, 1, 16, 2	9. S, 2, 7, 2	9. S, 3, 16, 2
10. S, 4, 3, 2	10. H	10. S, 4, 7, 2	10. H
11. R, 3, 3, 2		11. R, 1, 4, 2
12. T, 1, 0		12. T, 1, 0
13. R, 3, 8, 2		13. R, 1, 9, 2
14. T, 1, 0		14. T, 1, 0
15. O, 1, 3		15. O, 2, 3
16. R, 2, 9, 2		16. R, 4, 9, 2
17. O, 1, 3		17. O, 2, 3
18. H		18. H

Рисунок 1 - РВС умножения матрицы 4´4 с распределенным двухточечным вводом-выводом и циркулярной передачей столбцов матрицы-множителя

В качестве второго варианта (рисунок 2) рассмотрим РВС, отличающуюся от предыдущей порядком ввода и обработки столбцов матрицы B: программа, вводящая исходные данные, сначала обрабатывает первый (по порядку ввода) свой столбец, а затем второй (по порядку ввода) столбец матрицы B, принятый от соседней программы, вводящей исходные данные.

k=m=1	k=m=2	k=m=3	k=m=4
1. I, 1, 2	1. R, 1, 3, 2	1. I, 2, 2	1. R, 1, 5, 2
2. T, 1, 0	2. T, 1, 0	2. T, 1, 0	2. T, 1, 0
3. S, 2, 1, 2	3. R, 1, 10, 2	3. S, 1, 13, 2	3. R, 1, 12, 2
4. S, 3, 13, 2	4. T, 1, 0	4. S, 2, 5, 2	4. T, 1, 0
5. S, 4, 1, 2	5. R, 3, 4, 2	5. S, 4, 5, 2	5. R, 3, 5, 2
6. R, 3, 10, 2	6. T, 1, 0	6. R, 1, 11, 2	6. T, 1, 0
7. T, 1, 0	7. R, 3, 11, 2	7. T, 1, 0	7. R, 3, 12, 2
8. I, 1, 2	8. T, 1, 0	8. I, 2, 2	8. T, 1, 0
9. T, 1, 0	9. S, 1, 16, 2	9. T, 1, 0	9. S, 3, 16, 2
10. S, 2, 3, 2	10. H	10. S, 1, 6, 2	10. H
11. S, 3, 6, 2		11. S, 2, 7, 2
12. S, 4, 3, 2		12. S, 4, 7, 2
13. R, 3, 3, 2		13. R, 1, 4, 2
14. T, 1, 0		14. T, 1, 0
15. O, 1, 3		15. O, 2, 3
16. R, 2, 9, 2		16. R, 4, 9, 2
17. O, 1, 3		17. O, 2, 3
18. H		18. H

Рисунок 2 - Нереализуемый вариант РВС умножения матрицы 4´4

с распределенным двухточечным вводом-выводом

Регулярную вычислительную схему назовем реализуемой, если каждая из входящих в нее программ, начав выполняться, через конечное время завершится остановом, вызванным соответствующей командой HALT.

Возможность создания сложных РВС делает необходимой формулировку условий реализуемости произвольных регулярных схем. Для анализа реализуемости РВС используем граф, отображающий существующие в ней зависимости между командами посылки/приема сообщений.

Графом зависимостей РВС назовем ориентированный граф DG(V,U), множество вершин V которого взаимнооднозначно соответствует множеству команд посылки (SEND) и приема (RESEIVE) сообщений схемы, а множество дуг U формируется на основании следующего правила. Пусть вершины v¢ Î V и v¢¢ Î V графа зависимостей DG(V,U) соответствуют командам c¢.j¢ и c¢¢.j¢¢ регулярной вычислительной схемы. Тогда дуга áv¢,v¢¢ñ принадлежит множеству U в том и только том случае, если команды c¢.j¢, c¢¢.j¢¢ либо образуют пару отправитель-получатель, либо входят в одну и ту же командную последовательность так, что c¢.j¢ предшествует c¢¢.j¢¢ и не существует команд посылки/приема сообщений, находящихся в последовательности между рассматриваемыми командами c¢.j¢ и c¢¢.j¢¢.

Утверждение.

Необходимым и достаточным условием реализуемости регулярной вычислительной схемы является отсутствие контуров в ее графе зависимостей.

Множество реализуемых РВС определим как множество схем, имеющих ациклические графы зависимостей.

На рисунке 3 представлены графы зависимостей РВС, рассмотренных в примерах 1 и 2

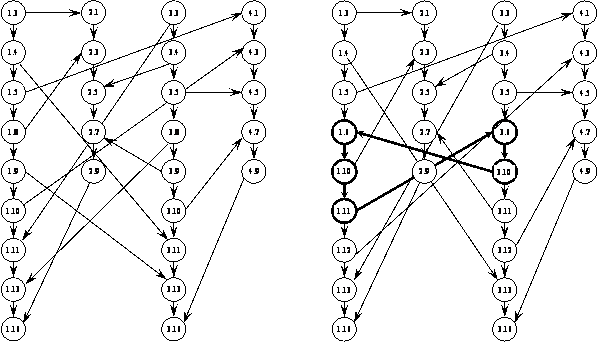
Рисунок 3 - Графы зависимостей РВС, показанные на рисунках 1 и 2

Анализ графов показывает, что РВС первого варианта (рисунок 1) реализуема, поскольку ее граф зависимостей не имеет контуров. РВС второго варианта (рисунок 2) нереализуема, так как ее граф зависимостей имеет контур 1.6 –1.11 – 3.6 – 3.10, выделенный утолщенными линиями.

ЛИТЕРАТУРА

1. Немнюгин С.А., Стесик О.Л. Параллельное программирование для многопроцессорных вычислительных систем. – СПб.: БХВ-Петербург, 2002. – 400 с.

2. Распределенные конвейерные вычисления: модели, свойства, реализация и применение. Отчет о НИР. Руководитель работы И.И.Ладыгин – № ГР 010200001482. – М.: МЭИ, 2003. –101 с.