АЛГОРИТМ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

МЕТОДОМ ТАНГЕНСОВ

Л.И. Абросимов, К.В. Султанов

(г. Москва, Московский энергетический институт (Технический университет), Россия )

Определение производительности вычислительных сетей, которое рассмотрено в предыдущей статье этого раздела (7-1) предусматривает использование метода контуров [1, 2], в соответствии с которым составляются и решаются системы линейных и нелинейных уравнений.

Нелинейные уравнения являются частью аналитической модели и составляются для каждого контура. Совместное их решение позволяет определить базовые интенсивности l₀_q для потоков всех контуров сети.

Основой составления уравнений является условие, что в установившемся режиме количество сообщений в одном контуре не изменяется и равно сумме математических ожиданий сообщений в каждом узле данного контура.

Тогда в соответствии с [1, 2] для каждого контура можно записать нелинейное уравнение:

, где k_i Î q, (1)

где:

n_q – количество сообщений в одном контуре,

l - интенсивность поступления сообщений,

m - интенсивность обслуживания сообщений в узле.,

При расчёте характеристик замкнутых систем необходимо использовать коэффициент ограниченности очереди:

Формулировка задачи

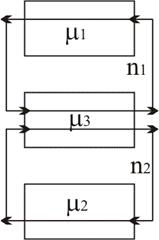В качестве примера, рассмотрим простую систему с тремя узлами и двумя замкнутыми контурами (рис. 1). Контур q =1 обслуживают узлы 1 и 3, контур q =2 обслуживают узлы 2 и 3. Для рассматриваемой системы необходимо рассчитать интенсивности l_q поступления сообщений.

рис. 1

В соответствии с (1) можно записать систему нелинейных уравнений:

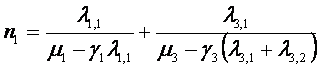(2)

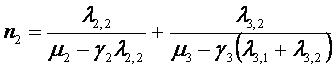
где l_i_,_q интенсивность поступления в i-й узел сообщений q-го контура

Для рассматриваемого примера l_1,1 = l_3,1 = l₁; l_2,2 = l_3,2 = l₂

Таким образом, имеем систему из Q уравнений () c Q неизвестными базисными интенсивностями l_q.

Целью решения нелинейных уравнений является вычисление базисных интенсивностей l_q для каждого контура q.

Алгоритм решения системы нелинейных уравнений.

Алгоритм выполняется в 2 этапа.

На 1-м этапе для первого уравнения принимаем:

l_q= l₁ для всех и выполняем решение этого уравнения пошаговым методом тангенсов и находим для 1-ой итерации значение l₁^’

Далее, для каждого q-го уравнения подставляем фиксированные значения:

l^’₁, l^’₂, ... l^’_q_-1 для уже найденных интенсивностей, принимаем

l_q= l_q₊₁= = l_Q для всех не вычисленных интенсивностей и находим итерации значение l_q^’ .

Вычисления 1-го этапа производятся для всех Q уравнений.

Второй этап начинается после того как вычислены значения всех интенсивностей l^’₁, l^’₂, ... l^’_Q. При решении каждого уравнения на каждой последующей итерации определяется значение интенсивности l_q^'' соответствующей итерации, при этом значения остальных интенсивностей рассматриваются как фиксированные, численно равные значениям последних итераций этих интенсивностей.

Для решения каждого нелинейного уравнения будем использовать пошаговый метод тангенсов. Для этого представим каждое нелинейное уравнение (1) в канонической форме:

(3)

Каноническая форма нелинейного уравнения (3) изображена на рис 2.

Решению соответствует корень уравнения при

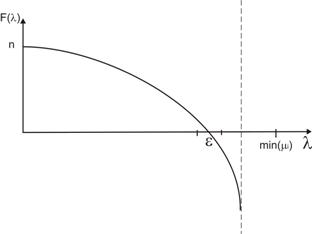
рис. 2

1) Решение одного уравнения пошаговым методом тангенса:

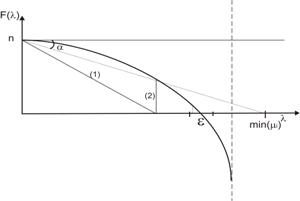
Начальной точкой итеративной процедуры (шаг s=0) является точка , в которой ; (см. рисунок 3).

На шаге s = 1 из точки проводим линию (1), наклон которой определяется коэффициентом , равным отношению к F()/

Для s=0, ; ; 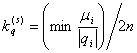, где

- интенсивность обслуживания сообщений в i -ом узле,

|q_i|- количество контуров в i -ом узле,

n- количество сообщений в q -ом контуре.

На каждом s-ом шаге этого этапа алгоритма используются соотношения (4 и 5)

(4)

(5)

В результате вычислений возможна ситуация выхода из зоны допустимых решений, признаком этого является значение < 0. Рис. 3

В этом случае необходимо применять коррекцию k⁽^s_q⁾:

То есть, если , тогда и (6)

Если , тогда

2) Решение системы уравнений

2.1) l₁=l₂=…=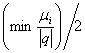

Далее решаем все уравнения в соответствии с п. 1, и находим l`₁,l`₂…

2.2) Последовательное решение каждого уравнения

- берём уравнение для первого контура фиксируем l₂=l`₂ и ищем l``₁ в соответствии с п. 1;

- берём уравнение для второго контура фиксируем l₁=l``₁ и ищем l``₂ в соответствии с п. 1;

2.3) Циклически выполняем п. 2.2 пока не будет достигнута точность e.

Условие окончания цикла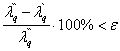

ПРИМЕР (см. рисунок 1)

Для конура q = 1, n₁ = 4, m₁ = 10;

для контура q = 2, n₂ = 8, m₂ = 10;

точность вычисления e = 0,05

По соотношению вычисляем g_I:

g₁ = 3/4; g₂ = 7/8; g₃ = 11/12;

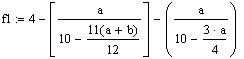
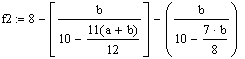
Где a = λ1, b = λ2

0) λ1 = λ2 = µ/2 = 5

k1(0) = 5/(4*2) = 0.625

k2(0) = 5/(8*2) = 0.3125

1) зафиксируем λ2 = 5

λ1 = 4*0,625 = 2.5

f1 = 2.892

2) λ2 = 5

λ1 = 2.5 + 2.892*0.625 = 4.3

f1 = 0.45

3) λ2 = 5

λ1 = 4.3 + 0.45*0.625 = 4.58

f1 = - 0.457

4) λ2 = 5

k1 = k1(0)/2 = 0.3125

λ1 = 4.3 + 0.45*0.3125 = 4.44

f1 = 0.037

| λ1(2) – λ1(4)| / λ1(4) = 0.03 < 0.05

5) зафиксируем λ1 = 4.44

λ2 = 8*0,3125 = 2.5

f2 = 6.993

6) λ1 = 4.44

λ2 = 2.5 + 6.993*0.3125 = 4.69

f2 = 4.329

7) λ1 = 4.44

λ2 = 4.69 + 4.329*0.3125 = 6.04

f2 = - 8.637

8) λ1 = 4.44

k2 = k2(0)/2 = 0.15625

λ2 = 4.69 + 4.329*0.15625 = 5.37

f2 = 1.657

9) λ1 = 4.44

λ2 = 5.37 + 1.657*0.15625 = 5.63

f2 = - 0.429

10)λ1 = 4.44

k2 = k2(8)/2 = 0.078

λ2 = 5.37 + 1.657*0.078 = 5.5

f2 = 0.748

| λ2(8) – λ2(10)| / λ2(10) = 0.02 < 0.05

1”) зафиксируем λ2 = 5.5

λ1 = 4*0,625 = 2.5

f1 = 2.755

2”) λ2 = 5.5

λ1 = 2.5 + 2.755*0.625 = 4.22

f1 = - 0.489

3”) λ2 = 5.5

k1 = k1(0)/2 = 0.3125

λ1 = 2.5 + 2.755*0.3125 = 3.36

f1 = 1.762

4”) λ2 = 5.5

λ1 = 3.36 + 1.762*0.3125 = 3.91

f1 = 0.601

5”) λ2 = 5.5

λ1 = 3.91 + 0.601*0.3125 = 4.097

f1 = 0.002

| λ1(4”) – λ1(5”)| / λ1(5”) = 0.046 < 0.05

6”) зафиксируем λ1 = 4.097

λ2 = 8*0,3125 = 2.5

f2 = 7,048

7”) λ1 = 4,097

λ2 = 2,5 + 7,048*0.3125 = 4,7

f2 = 4,774

8”) λ1 = 4,097

λ2 = 4,7 + 4,774*0.3125 = 6,19

f2 = - 4,205

9”) λ1 = 4,097

k2 = k2(0)/2 = 0.15625

λ2 = 4,7 + 4,774*0.15625 = 5,45

f2 = 2,593

10”) λ1 = 4,097

λ2 = 5,45 + 2,593*0.15625 = 5,855

f2 = 0,126

11”) λ1 = 4,097

λ2 = 5,855 + 0,126*0.15625 = 5,87

f2 = - 0,004

12”) λ1 = 4,097

k2 = k2(9”)/2 = 0.078

λ2 = 5,855 + 0,126*0.078 = 5,86

f2 = 0,083

| λ2(10”) – λ2(12”)| / λ2(12”) = 0.002 < 0.05

1’’’) зафиксируем λ2 = 5.86

λ1 = 4*0,625 = 2.5

f1 = 2.622

2’’’) λ2 = 5.86

λ1 = 2.5 + 2.622*0.625 = 4.14

f1 = - 1.568

3’’’) λ2 = 5.86

k1 = k1(0)/2 = 0.3125

λ1 = 2.5 + 2.622*0.3125 = 3.32

f1 = 1.463

4’’’) λ2 = 5.86

λ1 = 3.32 + 1.463*0.3125 = 3.78

f1 = 0.223

5’’’) λ2 = 5.86

λ1 = 3.78 + 0.223*0.3125 = 3.85

f1 = -0.044

6’’’) λ2 = 5.86

k1 = k1(3’’’)/2 = 0.15625

λ1 = 3.78 + 0.223*0.15625 = 3.81

f1 = 0.112

| λ1(4”’) – λ1(6’”)| / λ1(6’”) = 0.008 < 0.05

7’’’) зафиксируем λ1 = 3.81

λ2 = 8*0,3125 = 2.5

f2 = 7,087

8’’’) λ1 = 3.81

λ2 = 2,5 + 7,087*0.3125 = 4,71

f2 = 5.048

9’’’) λ1 = 3.81

λ2 = 4.71 + 5.048*0.3125 = 6.29

f2 = - 1.88

10’’’) λ1 = 3.81

k2 = k2(0)/2 = 0.15625

λ2 = 4,71 + 5.048*0.15625 = 5,5

f2 = 3.188

11’’’) λ1 = 3.81

λ2 = 5.5 + 3.188*0.15625 = 5,998

f2 = 0.795

12’’’) λ1 = 3.81

λ2 = 5.998 + 0.795*0.15625 = 6.12

f2 = -0.136

13’’’) λ1 = 3.81

k2 = k2(10’”)/2 = 0.078

λ2 = 5.998 + 0.795*0.078 = 6.06

f2 = 0.348

| λ2(11’”) – λ2(13’”)| / λ2(13’”) = 0.009 < 0.05

1””) зафиксируем λ2 = 6.06

λ1 = 4*0,625 = 2.5

f1 = 2.531

2””) λ2 = 6.06

λ1 = 2.5 + 2.531*0.625 = 4.08

f1 = - 2.375

3””) λ2 = 6.06

k1 = k1(0)/2 = 0.3125

λ1 = 2.5 + 2.531*0.3125 = 3.29

f1 = 1.261

4””) λ2 = 6.06

λ1 = 3.29 + 1.261*0.3125 = 3.68

f1 = 0.058

5””) λ2 = 6.06

λ1 = 3.68 + 0.058*0.3125 = 3.698

f1 = -0.016

6””) λ2 = 6.06

k1 = k1(3””)/2 = 0.15625

λ1 = 3.68 + 0.058*0.15625 = 3.689

f1 = 0.021

| λ1(4””) – λ1(6””)| / λ1(6””) = 0.002 < 0.05

| λ1(””) – λ1(‘”)| / λ1(””) = 0.032 < 0.05

| λ2(’”) – λ2(”)| / λ2(’”) = 0.033 < 0.05

λ2 = 6.06

λ1 = 3.689

Результат сходимости алгоритма представлен на рисунке 4.

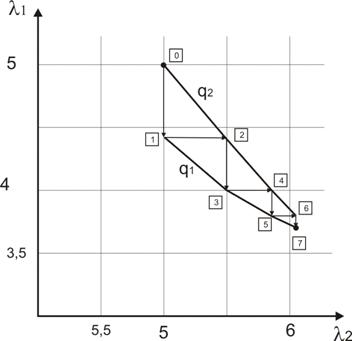
Рис.4

Литература

1 Абросимов Л.И. Анализ и проектирование вычислительных сетей: Учебное пособие - М.:, Изд-во МЭИ. 2000. - 52 с.

2 Абросимов Л.И. Модели и методы для оценки качества сетевого функционирования. Электронный журнал «Вычислительные сети. Теория и практика (BC/NW)». Номер 1 2001(1)

http://network-journal.mpei.ac.ru/cgi-bin/main.pl?l=ru&n=1&pa=4