Шевченко И.В. (МЭИ)
КОМПОЗИЦИИ БЫСТРЫХ АЛГОРИТМОВ СОРТИРОВКИ
Исследуются композиции быстродействующихалгоритмов
сортировки, превосходящие базовые алгоритмы по производительности. Процедуры
сортировки публикуются впервые.
Сортировка как способ первичной обработки данных использовалась задолго до появления компьютеров, весьма широко применялась в первых поколениях компьютеров и до сих пор является важнейшим инструментом. Поэтому и оправданы усилия, направленные на ускорение сортировки. Вот что пишет об этом авторитетный специалист: «… можно с уверенностью заявить, что проблема эффективности сортировки остается сегодня такой же злободневной, как и ранее» [1] .
Аналитические исследования алгоритмов, обобщенные в [1], и экспериментальные данные свидетельствуют о том, что нет алгоритма сортировки, который можно безоговорочно признать лучшим. Если брать в расчет только ее производительность, то и тогда лучшие алгоритмы оказываются предпочтительными лишь в некоторой области значений характеристик сортируемого массива – параметров сортировки. Сочетая положительные свойства алгоритмов в их композиции, можно эту область расширить и даже добиться лучших показателей. Обозначив n число сортируемых записей, назовем их последовательность n-перестановкой. Все они с равной вероятностью 1/(n!) могут выступать в качестве исходной.
Традиционно оценки алгоритмов ориентированы на определение числа выполняемых операций*. Перемещения записей и сравнения их ключей – типичные операции сортировки. Сначала вкратце рассмотрим проблему минимизации числа перемещений. Существуют разные алгоритмы, накапливающие информацию о ключах записей, чтобы на заключительной стадии сортировки заменить исходную n-перестановку отсортированной. Прежде всего, это два принципиально различающиеся алгоритма вычисления адреса. Первый из них учитывает число инверсий каждой записи по отношению к прочим записям. Второй описан в [1, 3]. Обычные их реализации производят n перемещений записей в поле нового массива, и это – очевидный минимум. Больший интерес представляют реализации, столь же экономно (по времени) перераспределяющие записи в исходном массиве.
Оценим необходимое при перераспределении число перемещений, полагая ключи записей уникальными. Если известно новое положение всех записей, добиться его можно вытеснением записей: запись A вытесняет запись B, которая вытесняет запись C и т.д. вплоть до вытеснения некоторой записи L, претендующей на прежнее место записи A. В этот цикл вовлекается произвольное число записей от 1 до n.
Если какие-либо записи U, V, … , Z в первом цикле не участвовали, с одной из них начинается новый цикл и т.д. В конце концов, все записи займут требуемые позиции. Необходима хотя бы одна резервная позиция Rez.
Итак, рассматриваем сортировку как процесс замены исходной n-перестановки правильной (удовлетворяющей правилу сортировки).
Выгоднее проходить кольцо A – B – C – … – K – L – A в обратном направлении: перенести A в Rez, на место A поместить L и т.д. вплоть до переноса A из позиции Rez в позицию, освобожденную записью B. Этот вариант назовем циклом или кольцом замещений. Очевидно, каждая запись перемещается 1 раз, кроме записи A, перемещаемой дважды. Число записей в кольце назовем длиной кольца.
Если запись занимает в исходной и правильной n-перестановке одну и ту же позицию, имеем дело с вырожденным кольцом замещений. Вероятность p1 этого события для любой записи равна 1/n, поэтому среднее (по всем n-перестановкам) число таких колец равно 1 независимо от n.
Если все записи вовлечены в один цикл замещений, выполняется n+1 пересылка записей. Худший случай имеет место, если в каждом цикле участвуют лишь 2 записи, и требует 1,5n пересылок. Труднее выразить среднее число пересылок записей. Вначале оценим среднее число записей, участвующих в начальном кольце замещений. Так как p1 = 1/n, с вероятностью (n-1)/n в цикл вовлекается вторая запись, которая с вероятностью 1/(n-1) претендует на место отправной записи, поэтому вероятность p2 первого цикла, содержащего лишь 2 записи, также равна 1/n (перемножаем вероятности). Если иметь в виду, что позиции записей, вовлеченных в кольцо, кроме начальной, второй раз не могут быть выбраны, мы и для прочих возможных длин кольца получим вероятность 1/n. Отсюда находим значение (n+1)/2 для средней длины начального кольца, подтверждаемое экспериментом. Вырожденные кольца учитываются.
Данный результат порождает иллюзию того, что математическое ожидание Mn числа колец почти равно log2n, однако эта величина даже не является строгой верхней границей Mn.
Лемма 1. Математическое ожидание Mn является гармоническим числом Hn. Обозначим Pj вероятность получения правильной n-перестановки в результате выполнения j циклов замещений; ∑ Pj = 1. На полных множествах n-перестановок для n = 2 .. 30 были вычислены Pj и получены Mn = ∑ j Pj, точно совпадающие с гармоническими числами Hn = ∑ 1/j.
Быстродействие
программы не позволило найти Mn для n > 30, поэтому для n = 40, 100, 1000, 10000,
100000, 1000000, 10000000 на
псевдослучайных множествах n-перестановок проведено
компьютерное статистическое исследование,
подтвердившее совпадение Mn и Hn
с высокой степенью точности.
Доказать лемму
1 можно также заметив, что математическое ожидание числа циклов длины k в перестановке n элементов равно 1/k. Это действительно так,
поскольку элементы k-цикла
можно выбрать ![]() способами. Фиксируя
первый элемент цикла, различные циклы можно получить (k-1)! способами, а оставшиеся (не
входящие в цикл элементы) можно переставить (n-k)! способами. Отсюда
непосредственно следует, что общее число циклов длины k равно
способами. Фиксируя
первый элемент цикла, различные циклы можно получить (k-1)! способами, а оставшиеся (не
входящие в цикл элементы) можно переставить (n-k)! способами. Отсюда
непосредственно следует, что общее число циклов длины k равно
![]()
и их математическое ожидание равно соответственно 1/k.
Из последнего факта и вытекает, что
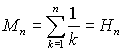
Лемма 1 позволяет дать оценку средней вычислительной сложности переписки записей в исходном массиве (физического упорядочения), завершающей сортировку по алгоритму, который оперирует множеством курсоров – ссылок на записи. Такие алгоритмы называют списковыми, ибо курсоры образуют тот или иной список. Кольца замещений применяются и в других алгоритмах. Поэтому полученный результат нужен для оценки вычислительной сложности множества алгоритмов. Для вычислений удобно следующее приближение
Hn ≈ ln n
+ γ + 1/(2n) – 1/(12 n2) + 1/(120 n4)
или – при больших n
Hn ≈ ln n + γ, где γ ≈ 0,577 – постоянная Эйлера.
Лемма 2. Математическое ожидание числа перемещений записей при перестроении исходной n-перестановки в правильную, равно n + Hn – 2. Каждая запись однажды перемещается – в одном из Hn колец, но «отправная» запись кольца перемещается 2 раза: в позицию Rez и из нее. Поэтому на каждое из Hn колец приходится дополнительное перемещение. Мы вычитаем 2, ибо для вырожденного кольца (его математическое ожидание 1) перемещение записи в Rez и обратно не выполняем. Эксперимент подтверждает оценку.
Существуют алгоритмы, которые в случае повторяемости значений ключа дают меньшее среднее число циклов замещений.
Рассмотрим теперь проблему минимизации числа сравнений записей. Если алгоритм не использует исходной или накопленной информации о множестве ключей, нижней гранью среднего числа сравнений при сортировке является O(log(n!)). Это мера исходной неопределенности массива, рассматриваемого как система с n! равновероятными состояниями (n! – число перестановок).
Метод, использующий сравнения сортируемых ключей, назовем сопоставительным. В этом методе БыстрСорт [2] – один из самых быстрых алгоритмов, рассматриваемый обычно как эталон. Отобразительный метод упорядочения [3] не требует сравнений ключей. Ключи используются для отображения на вектор: вектор позиций, занятых массивом, или вектор счетчиков, либо вектор голов цепных списков, предназначенных для сцепления записей с равным значением ключа. Перераспределение записей в массиве или списке является вторым этапом. Метод требует дополнительной памяти. Если ключ, например ключ-строка, длинный, то либо затрачивается слишком большая память, либо отображение каждой записи выполняется по частям ключа, несколько раз. И в том, и в другом случае преимущество метода по времени сортировки уменьшается или совсем исчезает.
Возможен компромисс: начало сортировки выполняется методом отображения по старшей части K ключа для получения значительной (хотя и не полной) упорядоченности. Это первая фаза сортировки. Записи с равным значением K оказываются соседними. Наводит полный порядок в полученных группах записей сопоставительный алгоритм сортировки. Это вторая фаза.
Рассмотрим пример. Пусть в массиве будет 500 000 записей с составным ключом, старшая часть K которого – поле целого типа. Его значения положительны и максимум равен 50 000. Пропуски значений возможны, распределение ключей равномерное. Мера исходной неопределенности Hi = log2(500000!) ≈ 500000 log2500000 ≈ 9 465 784 битов. После отображения и расстановки возникнет не более 50 000 групп записей, содержащих в среднем по 10 с небольшим записей. Мера неопределенности станет приблизительно равна Hnew = 50000·10· log210 ≈ 1 660 960 битов. Следовательно, получение этих групп сопоставительным методом потребовало бы в среднем ≈ 9 465 784 – 1 660 960 = 7 804 824 сравнений и пропорциональное число перемещений записей; этот минимум не достигается даже в лучших алгоритмах. Поэтому предполагаем, что отобразительный метод формирует группы гораздо быстрее.
Композиция 1. Процедура Comp1 реализует отобразительное упорядочение (фазу 1) с помощью счетчиков, используя на фазе 2 БыстрСорт для сортировки в группах. В обращении к ней указываются массив X сортируемых записей и наибольшее целое значение Verh старшей части key ключа сортировки. Логика сравнения следующих частей ключа записывается как пользовательская функция f логического типа. Функция f используется в БыстрСорт.
Наименьшее значение Niz ключа может быть указано в обращении. Если значение Niz не дано, по умолчанию принимается Niz = 0. Каждому значению z ключа отведен счетчик Sz, группу записей с таким ключом назовем группой “z”. Вначале все Sz = 0.
В начале фазы 1 каждая запись X[k] «находит» счетчик SX[k].key – Niz; к нему прибавляется 1. Так производится подсчет равных записей. Затем счетчики Sz заменяются будущими границами групп в отсортированном массиве. Для этого счетчики суммируются. Например, если в массиве X два нулевых значения ключа, вообще нет значений «1», «2» и четыре значения «3», то верхней границей группы записей с ключом «0» будет 2-я позиция, а верхней границей группы записей с ключом «3» – 6-я позиция. Это внешние границы.
Записи рассматриваются вновь и размещаются в том же массиве X в соответствии с полученной информацией: по мере появления ключей «0» будут заняты позиции 1 и 0, по мере появления ключей «3» занимаются позиции 5, 4, 3, 2 и т. п. Устанавливаемые записи вытесняют записи, изначально находившиеся в этих позициях, обмениваясь с ними местами. На этом этапе каждый элемент Sz используется как текущий указатель позиции в соответствующей группе “z”.
Способ расстановки записей, реализуемый For-циклом, внутри которого Repeat-цикл, является новым, наименее очевиден, поэтому требует разъяснений.
Type zap =
Record key, key1, key2: integer;
z:Array[1..10] of integer end;
Fun = Function (var A, B: zap):
Boolean; // key – старший ключ записи,
Var X:
Array[0..100000] of zap;
// key1 – средний, key2 – младший ключ
Function f
(var A, B: zap): Boolean;
begin
f:=(A.key1 < B.key1) or (A.key1 = B.key1) and (A.key2 < B.key2) end;
Procedure
Comp1 (Var X: Array of zap; f: fun; Verh: integer; Niz: integer = 0);
Var S: Array of integer; h, i, j, k, q, z: integer; u, w: zap;
Procedure Sort(L, R: integer); // БыстрСорт – для сортировки в группах
Var i, j: integer;
begin i:=
L; j:= R; u:= X[(L+R) div 2];
Repeat
While f (X[i],u) do Inc(i); While f (u, X[j]) do Dec(j);
If i <= j then begin w:= X[i]; X[i]:=
X[j]; X[j]:= w; Inc(i); Dec(j) end
Until i > j;
If L
< j then Sort(L, j); If
i < R then Sort(i, R)
end;
begin h:=
High(X); q:= Verh – Niz; SetLength(S,
q+2);
For z:= 0 to q+1 do S[z]:= 0; // Установка в 0 всех счетчиков
For k:= 0 to h do Inc (S[X[k].key – Niz]); // Определение мощностей групп
For z:= 0 to q do Inc (S[z+1], S[z]); // Преобразование в таблицу границ
For k:= 0 to h do // Переписка записей – формирование групп
Repeat j:= X[k].key – Niz; i:= S[j] –1; // Цикл, реализующий кольцо обменов
If i < k then Break; S[j]:= i; u:= X[k]; X[k]:= X[i]; X[i]:= u
Until i = k;
For z:= 0 to q do If S[z+1] – S[z] > 1 then Sort(S[z], S[z+1] – 1)
end; //
Упорядочением в группах завершена сортировка
В For-цикле для k = 0, 1, 2, … , n-1 выполняется следующее:
А. Для записи, занимающей позицию k, определяется подлинное ее место в массиве – позиция i.
Б. Если i = k, запись уже находится в требуемой позиции, Repeat-цикл оканчивает работу.
В. Если i > k, происходит обмен i–й и k–й записей, возврат к п. А.
Таким образом выполняется кольцо замещений записей, использующих позицию k как своего рода перевалочный пункт. Ситуация i < k также имеет место и является особой ситуацией.
Лемма 3. Каждая позиция (каждая запись) может участвовать лишь в одном кольце замещений. Лемма непосредственно следует из логики алгоритма. Всякий раз при использовании позиции уменьшается на 1 ее номер, и эти изменения производятся в границах непересекающихся групп позиций, поэтому никакая позиция не может быть использована более одного раза.
Лемма 4. Значение true отношения i < k, является признаком записи, размещенной окончательно в одном из предыдущих колец замещений записей. Докажем это методом исключения. Ситуация i > k означает, что запись в k-й позиции претендует на позицию i, еще не участвовавшую в обменах (согласно лемме 3), а ситуация i = k означает, что эта запись изначально занимает требуемую позицию. В самом деле, если бы запись была перенесена в эту позицию ранее, то номер i был бы меньше k из-за вычитания 1 при каждом использовании позиции в текущей группе.
Лемма 5. Среднее число Mn колец замещений не превосходит Hn.
Если ключи записей уникальны, Mn = Hn по лемме 1. С увеличением частоты повторения ключей средняя длина колец замещений растет, значение Mn падает. Связано это с очередностью занятия позиций в группе: номера занимаемых позиций уменьшаются.
Проведем эксперимент. Обеспечим размер k > 1 начальной группы, поместив k наименьших ключей в случайные позиции массива, содержащего 100 псевдослучайных ключей. При сортировке массива определим длину D начального кольца замещений. Проделаем все это многократно и усредним D. Результат эксперимента отражен на Рис. 1.
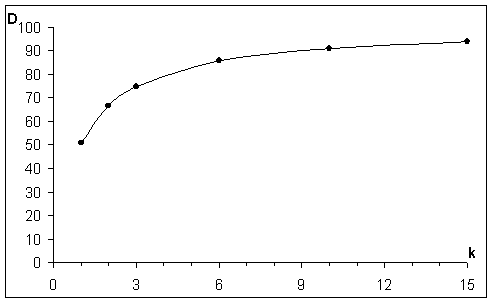
Рис. 1
Объясним его. Первое кольцо замещений не завершается, пока не будут установлены на свое место все k записей начальной группы, которые произвольно расположены в массиве и случайным образом вовлекаются в кольцо замещений. Заметное запаздывание этого события и влечет удлинение кольца. Его средняя длина примерно равна n·k/(k+1). Аналогичное влияние повторяемость ключей оказывает и на длину следующих колец замещений. В результате Mn уменьшается.
Вновь обратимся к процедуре Comp1. В ходе переписки записей текущие указатели Sz превращаются в указатели начал групп, что и используется при передаче групп алгоритму БыстрСорт (в завершающем процедуру For-цикле) для внутреннего упорядочения групп. Поскольку старшая часть key ключа в нем не требуется, в функции f, определяющей правило сортировки по составному ключу, фигурируют лишь имена key1, key2. Составных частей ключа может быть и больше, причем для каждой части можно задавать любое направление упорядочения: по возрастанию, по убыванию.
Испытания процедуры Comp1 на массивах с псевдослучайными ключами записей показали, что она в 1,5 – 2 раза быстрее процедуры QuickSort. Соотношение производительности двух указанных процедур зависит от размера записи, сложности ключа и отчасти от типа компьютера. На Рис. 2 дана серия графиков, отражающая зависимость времени сортировки от числа и размера rs сортируемых записей при трех составляющих ключа, имеющих целый тип.
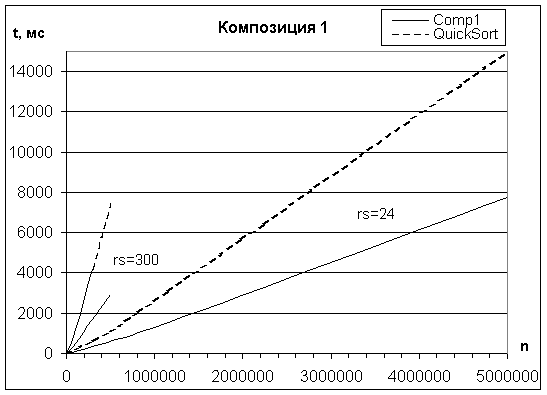
Рис. 2
Существует списковая реализация данной композиции алгоритмов, в которой перемещения записей заменены перемещениями курсоров. Это значительно уменьшает время сортировки записей большого размера.
Если заменить в процедуре Comp1 выделенный Repeat-цикл блоком
begin j:=
X[k].key – Niz; If S[j]-1 < k then Continue; Dec(S[j]);
While S[j] > k do // Используется небольшой вспомогательный массив b
begin w:= X[k]; t:=0; Repeat Inc(t); b[t]:=
S[j]; If S[j] = k then Break;
j:=
X[S[j]].key – Niz; Dec(S[j])
Until
t = High(b); X[k]:= X[b[t]];
For t:= t downto 2 do X[b[t]]:= X[b[t
–1]]; X[b[1]]:= w;
end
end;
то в кольцах замещений записей вместо обменов будут использоваться перемещения, что втрое уменьшает число присваиваний записей. При большой длине записей это заметно сказывается на времени первой фазы сортировки.
Данная программа, если в ней заключить в фигурные скобки последний For-цикл и процедуру Sort, выполняет вдвое быстрее, чем БыстрСорт, и сортировку по единственному ключу целого типа. Эффект уменьшается, если диапазон значений ключа превышает сотни тысяч. В этом случае рекомендуется отображение ключей, выполняемое в два этапа [3].
Композиция 2. Процедура Comp2 является аналогом Comp1, применяемым при сортировке записей по ключам – длинным строкам. Так как строки составлены из элементов, их первые символы могут быть использованы для отображения на вектор счетчиков с целью образования групп записей. В каждой группе эти символы одинаковы, размещение групп упорядочено, остается лишь получить словарный порядок внутри групп, используя оставшиеся символы строк.
Первым параметром процедуры является массив X записей, ключ key которых имеет тип string. Диапазон значений строк задается неявно: в обращении к Comp2 указывают символ symbol, код которого наименьший из числа используемых, кроме того, задают число m символов, идущих в таблице кода подряд, начиная с символа symbol. Например, если сортируются английские слова – строки без пробелов, содержащие лишь прописные буквы, записываем обращение Comp2(X, ‘A’, 26), а если есть и строчные буквы – даем обращение Comp2 (X, ‘A’, 57). Последний параметр равен 26 + 26 + 5 (между латинскими буквами есть 5 иных символов). Главное отличие Comp2 от Comp1 в логике – это специфическая формула получения номера счетчика.
Type zap =
Record key: string; u: Array[1..10] of
integer end; //поле u моделирует
Var X: Array[0..100000] of zap; // некоторое дополнительное содержание
Procedure
Comp2 (Var X: Array of zap; symbol: char; m: integer);
Var S: Array of integer; h, i, j, k, na, q, z: integer; w: zap;
Procedure Sort(L,R:integer);
Var i, j: integer; xx: string;
begin i:= L; j:= R; xx:= X[(L+R) div
2].key;
Repeat While X[i].key < xx do Inc(i); While xx < X[j].key do Dec(j);
If i <= j then begin w:= X[i];
X[i]:= X[j]; X[j]:= w; Inc(i); Dec(j) end
Until i > j;
If L < j then Sort(L, j); If i < R then Sort(i, R)
end;
begin h:= High (X); q:= Sqr (m); na:=
Ord(a); SetLength(S, q+1);
For z:= 0 to q do S[z]:= 0;
For k:= 0 to h do Inc(S[(Ord(X[k].key[1]) –
na)*m + Ord(X[k].key[2]) – na] );
For z:= 0 to q –1 do Inc(S[z +1], S[z]);
For k:= 0 to h do
Repeat j:= (Ord (X[k].key[1] ) – na)*m +
Ord (X[k].key[2]) – na; i:= S[j] –1;
If i < k then Break; S[j]:= i;
w:= X[k]; X[k]:= X[i]; X[i]:= w
Until i = k;
For z:= 0 to q –1 do If S[z+1] – S[z] > 1 then Sort (S[z],
S[z+1] –1)
end;
При сортировке ANSI-строк (длинных строк) перемещаются в памяти не строки, а ссылки на строки, поэтому списковый вариант данной композиции будет оправдан лишь в случае, если записи помимо ключа содержат большой объем иной информации и их физический размер велик.
Испытания процедуры Comp2 на массивах с псевдослучайными ключами записей показали, что она минимум в 1,5 раза быстрее процедуры QuickSort. Соотношение производительности двух данных процедур зависит от длины записи и отчасти от типа компьютера. Влияние длины ключа на время сортировки – слабое. На Рис. 3 дана серия графиков, отражающая зависимость времени сортировки от числа и размера rs сортируемых записей.
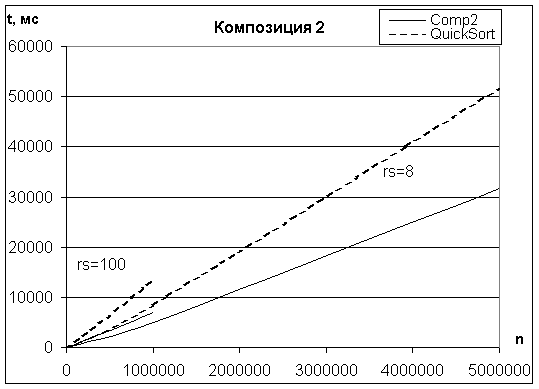
Рис. 3
В [3] приводится иная композиция алгоритмов, также предназначенная для сортировки записей по ключу-строке.
Данные композиции позволили сократить и число сравнений, и число перемещений записей за счет меньшего числа сложных действий, связанных с отображением записей.
Рассмотрим иные способы уменьшения затрат времени на перемещения сортируемых записей. Для бинарного слияния оценка среднего числа сравнений близка к оптимальной, однако оно проигрывает БыстрСорт по затратам на перемещения: при выполнении акта слияния все участвующие в нем записи переписываются на новое место. Сократить число этих актов (и перемещений) можно, переходя к t-арному слиянию, t >2. Число пересылок определяется выражением n élog t nù и падает с ростом t. На пути этого роста стоит проблема построения оптимальной универсальной схемы выбора наименьшего из t сравниваемых ключей, т.е. сохранение приемлемого числа сравнений. На завершающей стадии акта слияния t-арное слияние сменяется (t-1)-арным слиянием, (t-2)-арным слиянием и т.д., вплоть до бинарного слияния.
Пирамида, которую также называют сортдеревом, является относительно экономичной схемой выбора. Издержки времени, вызванные некоторым увеличением числа сравнений, с лихвой окупаются экономией на перемещениях при сортировке записей большого размера.
Композиция 3. Процедура Comp3 использует сортдерево, представленное массивами d, v, для выбора наименьшего из t ключей, взятых по одному из t сливаемых частей. Элементы d[j] являются ссылками на соответствующие записи. Подчиненная процедура Gruz служит и для построения сортдерева и для его восстановления после очередного изъятия корневого элемента. Элементы v[j] обозначают границы сливаемых упорядоченных частей.
Procedure Comp3 (Var X: Array of zap);
Const t = 230;
Var g, h, i, j, m, mp, n, s, u, z: integer; d, v: Array[1..t] of integer;
Procedure Gruz (j, dj, vj: integer);
// Погружение элемента, начиная от
корня
begin i:= j+j; While i < n do
begin If X[d[i+1]].key < X[d[i]].key
then Inc(i);
If X[dj].key <
X[d[i]].key then
begin d[j]:= dj; v[j]:= vj; Exit end;
d[j]:= d[i];
v[j]:= v[i]; j:= i; i:= i+i
end;
If
i = n then If X[dj].key >
X[d[i]].key then
begin d[j]:= d[i]; v[j]:= v[i];
j:= i end; d[j]:= dj; v[j]:= vj
end; // Конец
процедуры погружения в сортдерево элемента (dj, vj)
begin h:=
High(X) div 2; If h < 1 then
Exit; g:= h+1; m:= 1;
Repeat
mp:=
m; m:= m*t; u:= g; // Настройка на
этап слияния частей
If m > h then s:= 0 else s:= g – m + mp; // размером
mp
Repeat n:= 0; // Цикл, выполняющий все
акты слияния частей размером mp
Repeat Inc (n);
d[n]:= u;
Inc
(u, mp); // Формирование
массивов курсоров
If u >
g+h then begin v[n]:= g+h+1; Break
end; v[n]:= u
Until n = t; // Для одного акта
слияния массивы курсоров d,
v
заполнены
For j:= n div 2 downto 1 do Gruz (j, d[j], v[j]); // Построение
сортдерева
Repeat // Цикл, выполняющий один акт слияния t частей массива X
X[s]:=
X[d[1]]; Inc (s); Inc (d[1]);
If d[1]
= v[1] then begin j:= n; Dec (n)
end // Переход к меньшей арности
Else
j:=1; Gruz (1,
d[j], v[j])
Until n = 0 // Конец акта слияния
Until u > g+h; // Завершен этап слияния всех частей размером
mp
Dec (g,
m – mp)
// Изменение границы g в конце этапа
(данные перемещены)
Until m > h; // Окончание всех этапов слияния
end;
Особенностью данной реализации слияния является и то, что адреса результатов слияния насколько возможно приближены к адресам данных, участвующих в данном акте слияния. Число промахов мимо кэша сокращается за счет лучшей локальности алгоритма.
Сортируемый массив содержит 2n позиций для записей, в начале сортировки записи занимают n позиций в конце массива. С каждым новым этапом слияния вся совокупность записей смещается к началу массива так, что по завершении сортировки она занимает первые n позиций массива.
Композиция 3
рекомендуется для сортировки записей средней и большой длины, когда удельная
доля времени перемещений записей велика. На Рис. 4 показано, как при увеличении
длины записи растет время сортировки 1 млн записей. Время сортировки слиянием довольно стабильно. Этот фактор может
служить основанием предпочтения данной композиции перед БыстрСорт и в тех
случаях, когда выигрыш по времени не велик.
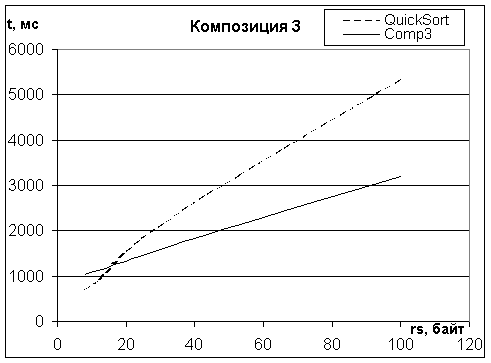
Рис. 4
По сути ту же самую композицию с добавлением процедуры внутренней сортировки, используем и для сортировки данных на винчестере, если используется лишь один физический диск. Именно на винчестере t-арное слияние дает максимальный эффект: сокращается число прогонов файла, а следовательно, и общий поток данных между винчестером и памятью.
Используя термин локальность для алгоритмов, работающих в памяти, мы предлагаем использовать слово компактность для характеристики размещения совместно используемых данных на винчестере. Рассматриваемая композиция отличается компактностью в смысле близости размещения записей - результатов слияния и записей, участвующих в данном акте слияния, что уменьшает ходы головки записи-чтения и экономит время.
Получение исходных упорядоченных частей файла в памяти выполняется любым быстродействующим алгоритмом. Мы применили БыстрСорт, указав вторым параметром длину e сортируемой части массива X. Полученные части записываются, начиная от конца файла, что автоматически удваивает его размер. Исходное пространство файла освобождается для записи результата сортировки. В ее конце производится усечение файла до первоначального размера.
Композиция 4. Для внутренней сортировки используется БыстрСорт, для выбора записей при слиянии на диске – сортдерево, организация слияния – t-арная. Параметр st задает полное имя файла, z – размер массива X, t – арность слияния.
Procedure Comp4 (st: string; z, t: integer);
Var f:
file; e, g, gg, h, i, j, k, m, mp, n,
nf, q, R, s, tr, u: integer;
X:
mas; d, v, c, w: Array of integer;
Procedure
Gruz (j, dj, vj: integer);
Var
i: integer;
begin
i:= j+j; While i <= n do
begin If i < n then If X[d[i+1]].key < X[d[i]].key
then Inc(i);
If X[dj].key <=
X[d[i]].key then Break;
d[j]:= d[i]; v[j]:= v[i];
j:= i; i:= i+i
end; d[j]:= dj; v[j]:=
vj
end;
begin
AssignFile(f,st); Reset(f, Sizeof(zap)); nf:= Filesize(f); m:= z;
j:=0; i:=0; k:= t+1;
Setlength(X,
z); Setlength(d, k); Setlength(v, k);
Setlength(c, k); SetLength(w, k);
Repeat
Seek(f,j); If nf-j < m then e:= nf-j else e:= m; // Цикл сортировки в памяти
BlockRead(f, X[0], e); QuickSort(X,e); Seek(f, j+nf);
BlockWrite
(f, X[0], e); Inc (j, e); Inc (i) //
Счетчик
i сортируемых частей
Until j = nf;
If i < t
then t:= i; g:= nf; R:= m div (t+1); tr:= t*R;
Repeat mp:= m;
m:= m* t; u:= g; gg:= g+nf; // Цикл прогонов файла
If m >= nf
then q:= 0 else q:= g – m + mp; // Курсор q места занесения в файл
Repeat n:= 0; // Цикл повторяющихся актов слияния
n частей файла
Repeat e:= R; If gg – u < R then e:= gg – u; c[n]:=u + e; // Подготовка к слиянию
Seek(f, u); h:=n*R; BlockRead(f, x[h], e);
w[n]:= u + mp; // Взятие порций
If gg – u < mp then w[n]:= gg; Inc(n);
d[n]:= h; v[n]:= h+e; // Запись курсоров
Inc(u, mp) //
Переход к следующей части файла
Until (n = t) or (u >= gg); // n - число сливаемых
частей; n <= t
For j:= n div 2 downto 1 do
Gruz
(j, d[j], v[j]); //
Построение сортдерева
s:= tr; // Курсор s
выходного буфера в массиве X
Repeat //
Цикл, выполняющий один акт слияния n частей файла
X[s]:= X[d[1]]; Inc(d[1]); Inc(s); j:= 1;
If
s = z then //Курсор
s совпал с внешней границей буфера записи; cброс в
begin e:= z
– tr; Seek(f, q); BlockWrite(f, X[tr], e); Inc(q, e); s:= tr end; // файл
If d[1] = v[1] then //
Курсор d[1] совпал с внешней границей
буфера чтения
begin
i:=
(v[1] –1) div R; //
Определение порции e
для чтения,
e:= w[i] – c[i]; If e > R then e:= R; // а если часть
исчерпана, уменьшается
If e = 0
then begin j:= n; Dec(n) end // текущая арность слияния n
Else
begin Seek (f, c[i]); BlockRead (f, X[i*R], e); // Взятие новой порции
Inc (c[i], e);
d[1]:=i*R; v[1]:= d[1]+ e end // Обновление курсоров
end;
Gruz (1, d[j], v[j]) // Погружение
в сортдерево нового элемента через корень
Until n = 0; e:= s
– tr;
Seek(f,
q); BlockWrite (f, X[tr], e); Inc (q, e) // Завершающий сброс
в файл
Until u >= gg;
Dec(g, m–mp) // Сдвиг границы g по окончании прогона
файла
Until m >= nf; // Завершение всех прогонов файла
Seek(f,
nf); Truncate (f) // Усечение файла до исходного
размера
end;
Полученная композиция обладает высокой
производительностью и в 1.8-2.5 раза опережает рассматриваемый в [3] алгоритм Paromsort. На Рис.5 приведен график времени
работы алгоритма для файлов размером до 10Гб (размер записи 100байт, размер
используемой памяти – 100Мбайт).
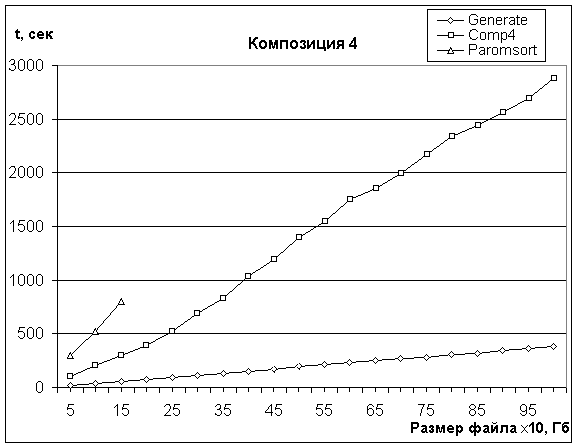
Рис. 5
Использование для сортировки данных в памяти t-арной пирамиды, как показали последние исследования, также существенно сокращает время сортировки больших записей. В пирамиде с увеличением t среднее число сравнений записей растет сильнее, чем в t-арном слиянии, использующем сортдерево, и тем не менее выигрыш во времени, по сравнению с БыстрСорт, может достигать 50 %. Пирамидальная сортировка также характеризуется большой стабильностью времени сортировки.
Рассмотренные композиции алгоритмов позволяют полнее использовать потенциал методов сортировки данных, и все заслуживают применения:
- процедура Comp1 – в случае целого типа старшей части сложного ключа;
- процедура Comp2 – при сортировке записей по ключу – длинной строке;
- процедура Comp3 – при произвольном типе ключа сортировки;
- процедура Comp4 – при сортировке файла записей на винчестере.
Как указывает Д. Кнут [1], композиции алгоритмов являются трудным объектом для анализа. Поэтому аналитические исследования приходится дополнять экспериментальными, что и было сделано при подготовке настоящей статьи.
Литература
Кнут Д.Э. Искусство программирования, том 3. Сортировка и поиск, 2-е изд.: Пер. с англ. М.: Изд. дом «Вильямс», 2000. – 822 с.: ил.
Hoare C.A.R. QuickSort. Comp. J., 5, № 1 (1962), 10-15.
Зубов В.С., Шевченко И.В. Структуры и методы обработки данных: Практикум в среде Delphi. – М.: Информационно-издательский дом «Филинъ», 2004. – 304 с.