МОДЕЛИ И МЕТОДЫ АНАЛИЗА СХОДСТВА ГРАФОВ ДЛЯ ПОИСКА СТРУКТУРНОЙ ИНФОРМАЦИИ

В.А. Кохов

(Москва, Московский энергетический институт (ТУ), Россия)

Выделены методы поиска информации, представленной графами. Методы основаны на определении сходства графов и их структурных инвариантов. Для быстрого и наиболее точного поиска по сходству предложена обобщённая иерархическая модель анализа сложности графов в монотонно расширяемых базисах структурных дескрипторов. Модель позволяет учитывать расположение фрагментов и обобщает известные методы характеризации графов.

Анализ методов поиска в информационно-поисковых системах структурной информации (ИПССИ) приводит к выделению двух основных подходов:

1. Методы, основанные на точной структурной характеризации графов:

1.1. Полная (установление изоморфизма графов).

1.2. Частичная (установление изоморфного вложения (не вложения)).

1.3. Подструктурная (определение максимального изоморфного пересечения графов).

1.4. Надструктурная (определение максимального изоморфного пересечения надграфов исходных графов).

2. Методы, основанные на приближённой структурной характеризации:

2.1. Полная (с точностью до IN-эквивалентности графов).

2.2. Частичная (с точностью до IN-эквивалентного вложения графов).

2.3. Подструктурная (с точностью до IN-эквивалентного пересечения).

2.4. Надструктурная (с точностью до IN-эквивалентного пересечения надграфов исходных графов).

Успех разработки новых ИПССИ зависит от развития теории сходства графовых моделей систем (ГМС) и разработки эффективных алгоритмов поиска одного или всех общих фрагментов во всех разновидностях поиска общих фрагментов ГМС и их структурных инвариантов (g-моделей) [1,2].

Рассмотрим пример анализа сходства по методу, основанному на точной структурной характеризации графов. В методе используются g-модели SHP^lScwÍP^lScw(G), называемые цветными графами цепей-подграфов (ЦГЦП).

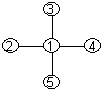
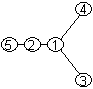
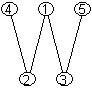
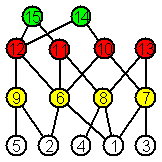
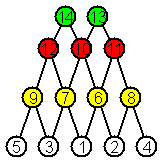
Примеры ЦГЦП для трёх графов приведены на рис. 1.

G1	G2	G3
ЦГЦП для G1	ЦГЦП для G2	ЦГЦП для G3

Рис. 1. Диаграммы графов и их цветных графов расположения цепей

Алгоритм построения ЦГЦП для графа G включает 7 шагов:

1. Исходный граф G является цветным ГЦП для цепей длины 0.

2. Для графа G cтроим 1-гомеоморфное расширение и получаем цветной ГЦП длины 1. Новые вершины v_iÎVP₁ отображают цепи длины 1 в графе G.

3. Каждую пару новых вершин v_i,v_j соединяем новым ребром {v_i,v_j}, если Гv_iÇГv_j ¹Æ.

4. Объединение цепей, соответствующих новым вершинам, порождает цепь-подграф в исходном графе G на 1 большей длины, чем длины объединяемых цепей.

5. Строим 1-гомеоморфное расширение новых ребер, порождая новые вершины, как цепи-подграфы длины 2 исходного графа G.

6. Повторяем выполнение п.3 и п.4 до тех пор, пока порождаются новые ребра, соответствующие цепям-подграфам исходного графа G.

7. Вершинам построенного графа приписываем цвет, номер которого соответствует длине цепи. В результате, построена g-модель HP^lScwÍP^lScw(G).

Аналогично строятся цветные графы цепей (ЦГЦ).

Определяя максимальное изоморфное пересечение ЦГЦП (MCS) или ЦГЦ (MCF) для каждой пары анализируемых графов, получаем два варианта вычисления расстояний и два варианта вычисления коэффициентов сходства:

• d₁(G₁,G₂) =úV(HP^lScwÍP^lScw(G₁))ê+úV(HP^lScwÍP^lScw(G₁))ê - 2úV(MCS)ê;

• d₂(G₁,G₂) =úV(HP^lcwÍP^lcw(G₁))ê+úE(HP^lcwÍP^lcw(G₁))ê+úV(HP^lcwÍP^lcw(G₂))ê+

+úE(HP^lcwÍP^lcw(G₂))ê- 2(úV(MCF)ê+úE(MCF)ê);

• MSI₁(G₁,G₂) =ú MCS(HP^lScwÍP^lScw(G₁),HP^lScwÍP^lScw(G₂))ê² /úF₁(G₁)×F₁(G₂)ê;

• MSI₂(G₁,G₂) =ú MCF(HP^lcwÍP^lcw(G₁),HP^lcwÍP^lcw(G₂))ê² /úF₂(G₁)×F₂(G₂)ê,

где F₁ (F₂) - число вершин (сумма числа вершин и рёбер) в ЦГЦП (ЦГЦ).

Для графов G₁- G₃ получим результаты, приведенные в табл. 1 (значения d₁,d₂ под главной диагональю, а значения MSI₁, MSI₂ - над диагональю).

Таблица 1

Цепи - подграфы (MSI1)								Цепи (MSI2)
	G1	G2	G3		ЦГЦ 1	ЦГЦ 2	ЦГЦ 3		G1	G2	G3		ЦГЦ 1	ЦГЦ 2	ЦГЦ 3
G1	0	0,64	0,36	ЦГЦ 1	0	0,53	0,48	G1	0	0,79	0,61	ЦГЦ 1	0	0,76	0,51
G2	2	0	0,64	ЦГЦ 2	8	0	0,69	G2	2	0	0,79	ЦГЦ 2	9	0	0,65
G3	4	2	0	ЦГЦ 3	9	5	0	G3	4	2	0	ЦГЦ 3	19	13	0

Переходя последовательно от ЦГЦ длины 0 к длине q, а затем к g-моделям, учитывающим расположение более сложных по индексам сложности фрагментов (например, деревья-подграфы и т.д.), получим универсальный метод для иерархического анализа сходства ГМС, с последовательным уточнением результатов. Данный метод включает в качестве частных случаев все 4 метода, образующие первый подход к методам поиска.

В табл. 2 приведены примеры матричного представления расширенной b-модели P^lScwÍP^Scw для G₂ и b-модели V^lÍP^Scw для HP^lcwÍP^lcw(G₂) [2].

Таблица 2

P^l^S^cwÍP^l^S^c	P0	P1	P2	P3	Irc(fi ^t)	Irc(f ^t(c))	Irc(f ^t)		V^lÍP^l^S^c		P0	P1		P2				P3			P4	Irc(fi ^t)		Irc(f ^t(c))
2	1	2	2	0	0,057	0,057	0,392	2		1			2		6				10	10			0,0648		0,0648
1	1	3	1	0	0,050	0,050		1		1			3		10				8	4			0,0350		0,0350
5	1	1	1	2	0,110	0,110		5		1			1		2				4	8			0,0451		0,0451
3,4	1	1	2	1	0,087	0,174		3,4		1			1		3				5	11			0,0613		0,1225
12	0	1	3	0	0,056	0,056	0,314	6		1			5		10				10	2			0,0285		0,0285
25	0	1	1	2	0,101	0,101		9		1			3		4				8	12			0,0710		0,0710
13,14	0	1	2	1	0,079	0,157		7,8		1			4		5				11	15			0,0901		0,1802
314	0	0	1	0	0,016	0,016	0,217	13		1			2		6				6	14			0,0784		0,0784
213,214	0	0	1	1	0,054	0,108		10,11		1			3		8				10	13			0,0802		0,1604
125	0	0	1	2	0,093	0,093		12		1			4		8				6	14			0,0795		0,0795
3125,4125	0	0	0	1	0,039	0,077	0,077	14,15		1			2		5				12	10			0,0672		0,1345
Slw	5	12	20	14	51	1	1	Slw		15			40		88				128	162			433		1
Sw	1	3	5	7	16	a(P0/P)=1		Sw			1		2			2			2		2		9		a(P0/P)=1
WF	5	4	4	2	15	a(P1/P)=1		WF			15		20				44		64		81		224		a(P1/P)=1
ISC(Pj)	1	3	9	31	44	a(P2/P)=1		ISC(Pj)			1		3				9		31		106		150		a(P2/P)=1
V_ISC	5	12	36	62	115	a(P3/P)=1		V_ISC			15		60				396		1984		8586		11041		a(P3/P)=1

Применение b-моделей позволяет провести иерархический анализ сходства графов в методах поиска второго подхода с последовательным уточнением результатов по каждому из двух следующих направлений исследований:

1. Индекс (ISC), вектор-индекс (V_ISC), матрица b-модели (M_Irc);

2. Вектор-индекс вкладов Irc(f ^t), Irc(f ^t(c)), Irc(f_i ^t), матрица M_Irc.

Вычисление максимального изоморфного пересечения (МИП) для каждой пары b-моделей в стратифицированной системе b-моделей, например

P^lwÍPw

®

P^lSwÍPw

®

P^lSwÍP^Sw

®

P^lScwÍP^Sw

®

P^lScwÍP^Scw

®

P^lScwÍP^Scw,

приводит к возможности исследования тенденций изменения сходства графов ещё по трём направлениям стратификации самой b-модели: (1) монотонное расширение базисов СД; (2) монотонное расширение типов фрагментов; (3) монотонное расширение как базисов, так и типов фрагментов графа.

В табл. 3 приведены значения расстояний по всем парам графов G₁-G₃ с использованием ISC, V_ISC и матриц M_Irc для b-моделей P^lcwÍP^cw при монотонном наращивании базиса СД от двух (P_0-1) до четырех (P_0-4) элементов.

Таблица 3

	ISC				V_ISC				M_Irc
Пары	P0-1	P0-2	P0-3	P0-4	P0-1	P0-2	P0-3	P0-4	P0-1	P0-2	P0-3	P0-4
G1,G2	0	18	44	44	0	18	80	80	210	2478	8058	8058
G1,G3	0	27	35	141	0	27	89	195	1260	10899	27639	49899
G2,G3	0	9	9	97	0	9	9	115	630	3465	9045	38725

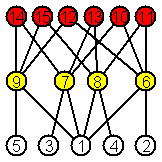
Построение графов сходства расположения фрагментов и определение их

МИП для каждой пары анализируемых графов делает возможным исследование сходства графов с учётом сходства расположения фрагментов заданного типа. На рис.1 приведен пример графа сходства расположения цепей для G₂, построенный на основе b-модели V^lÍP^Sc для HP^lScwÍP^Sc(G₂).

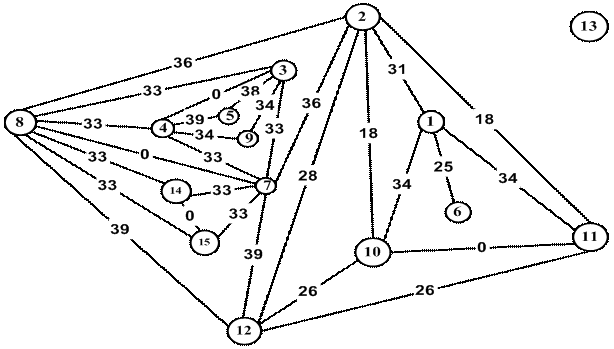
Рис. 1. Граф сходства расположения цепей в G₂ для расстояний не больших 0,4.

ЛИТЕРАТУРА

1. Кохов В.А. Методы анализа сходства систем с учетом расположения фрагментов. Тезисы докладов международной конференции «Информационные средства и технологии», МФИ-2003, Т1, Москва, МЭИ, 2003. – С.213-215.

2. Кохов В.А. Граф-модели в структурном спектральном анализе систем. Тезисы докладов международной конференции «Информационные средства и технологии», МФИ-2004, Т1, Москва, МЭИ, 2004. – С.211-214.