Метод организации вычислений с фиксированной точностью в модулярной арифметике.

Ш.А. Оцоков

(Москва, Московский энергетический институт (ТУ), Россия)

При составлении программ для решения инженерных задач основными требованиями являются достижение высокого быстродействия и необходимой точности результатов.

Известно, что ошибки округления, возникающие в процессе решения вычислительных задач на ЭВМ, могут привести к недопустимому снижению точности результатов.

Одним из способов получения конечного результата с требуемой точностью связан с применением модулярной арифметики.

Пусть множество входных данных (рациональные числа), с которыми проводятся арифметические операции: сложений, вычитаний, умножений и М - модуль системы остаточных классов [1,2].

Справедливо следующее утверждение:

Утверждение 1.

Пусть в ходе вычислительного процесса включающего в себя выполнение набора арифметических операций : сложений, вычитаний, умножений в поле рациональных чисел множества Х в системе остаточных классов с модулем М получен конечный результат .

Пусть известен знак искомого результата -равный ‘1’, если результат положительный, и ‘-1’, если отрицательный, а также значение определяемого в процессе арифметических операций в системе остаточных классов следующим образом:

и , тогда искомый результат определяется следующим образом:

Доказательство:

Пусть - дроби с которыми проводятся вычисления. Пусть требуется сложить дробей, тогда искомый результат P/Q по определению равен:

Найдем

Рассмотрим 2 случая.

1. случай. Если P/Q>0 и если B<M, то, тогда

2. случай. Если P/Q<0 и если B<M, то, тогда

Аналогично можно доказать и другие арифметические операции.

Ч.т.д.

Пусть - точность задания исходных данных, определяемая как количество верных цифр после запятой.

Очевидно, что максимальная точность конечного результата не может быть выше чем .

На основании этого утверждения разработан метод организации вычислений, обеспечивающий получение конечного результата с точностью , который по сравнению с существующим существенно расширяет диапазон представления рациональных чисел.

Суть данного метода заключается в следующем:

Пусть , - входные данные - числа с и соответственно цифрами после запятой, где и . M - модуль системы остаточных классов.

Представим и в следующем виде:

Тогда ,

,

Рассмотрим операцию сложения. Можно показать, что:

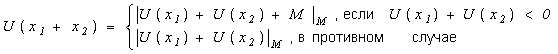
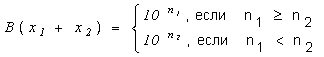
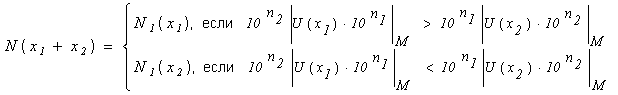
Операция вычитания аналогично сложению первого числа со вторым, но с противоположным знаком.

Рассмотрим операцию умножения. Можно показать, что:

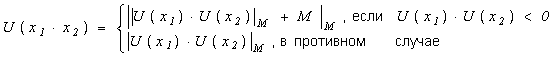
Рассмотрим операцию деления. Можно показать, что:

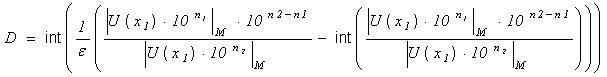
Пример. Найти значение выражения.

Каждое число будем представлять в виде тройки (U,B,N). Пусть модуль системы остаточных классов М=524269,

Имеем:

1. 0.89+0.5=89/100 + 5/10=1,39 или (99612,100, 1) + (262135,10,1) = (361747,100,1)

2. 1,39-23,875=-22,485 или (361747,100,1)-(327692,1000,1)=(34055,1000,-1)

3. -22,485+16=-6,485 или (34055,1000,-1) + (16,1,1) = (34071,1000,-1)

4. -6,485*2,5=-16,2125 или (34071,1000,-1) * (262137,10)=(347312,10000,-1)

5. -16,2125:5,095=-3,182041
или (347312,10000,-1): (128451,1000)= =-3,182041.

Разработанный метод позволяет существенно расширить диапазон представления рациональных чисел по сравнению с существующим в одномодульной системы остаточных классов [1].

Дальнейшим направлением развития данного метода является организация вычислений и с иррациональными числами на основе приближенного представления таких чисел в виде несократимых дробей с точностью задания исходных данных, а также распараллеливание вычислений в многомодульной системе остаточных классов.

ЛИТЕРАТУРА

1. Грегори Р, Кришнамурти Е. Безошибочные вычисления. Методы и приложения.М.:Мир,1988. –207 с.

2. Дзегелёнок И.И, Оцоков Ш.А. Подход к решению проблемы безошибочных вычислений с использованием ускоренного алгоритма отображения дробей Фарея. // Труды научной конференции, посвященной 75-летию со дня рождения академика В.А.Мельникова. РАН. М. 2004.