АЛГОРИТМ ПРОВЕРКИ СОГЛАСОВАННОСТИ МНОЖЕСТВА НЕТОЧНЫХ ТОЧЕЧНЫХ ВРЕМЕННЫХ ОГРАНИЧЕНИЙ

И.Е. Куриленко

(Москва, Московский энергетический институт (Технический университет), Россия)

Разработка способов представления информации, меняющейся со временем, и создание эффективных алгоритмов для рассуждений с учетом временного фактора решающе важны для современных интеллектуальных систем, к которым относится и ИСППР РВ [1,2].

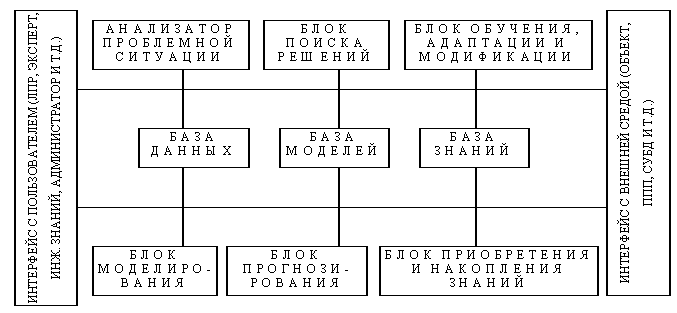
По сути, во всех основных блоках ИСППР РВ, включая базы данных и знаний, необходимо иметь средства представления фактора времени и временных (темпоральных) зависимостей, на основе которых моделируются и временные рассуждения. Базовый инструментарий для разработчика ИСППР РВ должен включать готовую реализацию системы временных рассуждений СВР [3], которая содержит средства представления и алгоритмы обработки временной информации.

Информация о времени традиционно представляется в виде временных зависимостей между временными примитивами [2]. В качестве таких примитивов могут использоваться временные моменты, интервалы или и то и другое. Зависимости между временными примитивами трактуются как ограничения на их расположение во времени.

Основная цель временных рассуждений состоит в порождении выводов из множества временных ограничений.

Обычно множество временных примитивов и отношений между ними представляется в виде задачи согласования ограничений (ЗСО), что позволяет использовать в решении задач временных рассуждений методы, применяемые для решения ЗСО.

Задача согласования временных ограничений (ЗСВО) состоит из:

1) конечного множества m временных переменных V = {,…},

2) области значений временных переменных - множества D,

3) конечного числа бинарных временных ограничений C = { | DxD}, где каждое ограничение – ограничение между временными переменными и .

Область значений переменных, соответствующих моментам времени и длительностям, D представляет собой множество чисел. Для интервальных переменных D – множество упорядоченных пар значений.

Отношения между временными переменными задаются на основе множества базовых временных отношений (BTR) между переменными – {| DxD}, причем:

1) отношения взаимно исключающие;

2) объединение всех элементов является универсальным ограничением U (U содержит все возможные отношения и, следовательно, не накладывает каких либо ограничений).

Неточное ограничение между переменными и это отношение вида {}, где , k>0 и . {} интерпретируется как . Единичным или точным называется ограничение, которое содержит один дизъюнкт. Задачу определения отношения, справедливого между переменными и , между которыми задано дизъюнктивное ограничение , называют задачей выявления неточного отношения. Единичной пометкой ограничения называется одно из отношений .

Единичную пометку ЗСВО, которая включает набор из k отношений, определяют как единичную пометку всех k ограничений. Решение ЗСВО - такой выбор отношений для каждого дизъюнктивного ограничения, что они не противоречат друг другу.

Известно, что решение ЗСВО для точечной модели времени с возможностью представления неточной информации является NP-полной задачей. Для проверки согласованности множества неточных точечных временных ограничений обычно используются алгоритмы поиска с возвратами. Будем рассматривать проблему проверки множества точечных ограничений, которое может содержать точные ограничения (T) и бинарные неточные ограничения (D) (PA-дизъюнкции). Известно, что в этом случае производительность алгоритма проверки согласованности может быть увеличена, за счет использования противоречий между точными и неточными временными ограничениями. В этом случае поиск согласующего сценария осуществляется в два этапа:

1) сокращение пространства поиска с помощью правил анализа PA-дизъюнкций;

2) выявление неточных отношений с помощью алгоритма поиска с возвратами.

Рассмотрим правила анализа PA-дизъюнкций [4]. Обозначим через T – исходное множество точных временных ограничений, а через Q-множества PA-резольвент. Приведенные ниже правила должны быть проверены для каждой PA-дизъюнкции D(i) в множестве PA-дизъюнкций D.

(1)	Выводимость (T-derivability) Если или , то дизъюнкция может не включаться в множество поиска D`.
(2)	Тавтология (T-tautology) a) Если добавление в T ограничения приводит к тому, что из T следует , то дизъюнкция может не включаться в множество поиска D`. b) Если добавление в T ограничения приводит к тому, что из T следует , то дизъюнкция может не включаться в множество поиска D`.
(3)	Резолюция (T-resolution) a) Если добавление в T ограничения не нарушает его согласованности, а добавление в T ограничения нарушает его согласованность, то исключить дизъюнкцию из множества поиска D`. Добавить в множество Q. б) Если добавление в T ограничения не нарушает его согласованности, а добавление в T связинарушает его согласованность, то исключить дизъюнкцию из множества поиска D`. Добавить в множество Q. в) Если внесение в T ограничения нарушает его согласованность и добавление в T связи нарушает его согласованность, то исходное множество ограничений несогласованно.

Приведенное ниже комбинированное правило предварительной обработки, позволяет уменьшить число запросов, которые необходимо выполнять для проверки каждой дизъюнкции, по сравнению с последовательным применением правил (1)-(3).

(4)

D Пусть отношение между моментами времени x и y, следуемое из множества T (). Аналогично - . Если сильнее или сильнее , то D(i) может быть исключена из множества D. Если =Ø и Ø, то D(i) должна быть исключена из множества D, {} должно быть добавлено к множеству Q. Если Ø и =Ø, то D(i) должна быть исключена из множества D, {} должно быть добавлено к множеству Q. Если =Ø и =Ø, то задача не имеет решения.

Алгоритм, построенный на основе этого правила, итеративно сокращает пространство поиска. На практике он показал лучшие результаты, чем алгоритм [4], основанный на применении правил (1)-(3) и был включен в состав прототипа СВР для ИСППР РВ на базе нетрадиционных логик разрабатываемой научной группой кафедры ПМ МЭИ под руководством Еремеева А.П.

ЛИТЕРАТУРА

1. Поспелов Д.А., Литвинцева Л.В «Представление знаний о времени и пространстве в интеллектуальных системах». - Под редакцией Д.А. Поспелова. – М.: Наука, 1986.

2. Еремеев А.П., Троицкий В.В. «Модели представления временных зависимостей в интеллектуальных системах поддержки принятия решений» - Изв. РАН. Теория и системы управления. 2003, № 5, с. 75-88.

3. Еремеев А.П., Куриленко И.Е. «Реализация временных рассуждений для интеллектуальных систем поддержки принятия решений реального времени» - «Программные продукты и системы», №2.

4. Gereveni A, Schubert. L. «An efficient method for managing disjunctions in qualitative temporal reasoning» - In principles of knowledge representation and reasoning: Proceedings of the Fourth International Conference, San Francisco, CA, 1994.