ПАРАЛЛЕЛЬНАЯ РЕАЛИЗАЦИЯ МЕТОДА ПАЛЬЦЕРА-МАНОЛОПОЛИСА ДЛЯ ВЫЧИСЛЕНИЯ МАТРИЦЫ ПЛОТНОСТИ В ЗАДАЧАХ РАСЧЕТА ЭЛЕКТРОННОЙ СТРУКТУРЫ МОЛЕКУЛ

А.М.Чернецов, О.Ю. Шамаева

(Москва, Московский энергетический институт (Технический университет), Россия)

В докладе представлены результаты параллельного расчета молекулярных систем большой размерности с использованием класса полуэмпирических методов нулевого дифференциального перекрывания на кластерных системах.

Расчеты электронной структуры гигантских молекул являются одними из самых сложных в современной науке и требуют использования высокопроизводительных вычислительных средств таких как суперЭВМ и кластерные установки. Расчеты электронной структуры, в частности, биомолекул (белков, ДНК) и наночастиц, актуальны для ряда областей науки: химии, биохимии, физики конденсированного состояния вещества и др. В практическом плане эти расчеты важны для фармакологии, нанотехнологий, исследований явлений сверхпроводимости и др.

Основными методами расчетов электронной структуры молекул являются неэмпирические и полуэмпирические методы квантовой химии. Неэмпирические методы расчета требуют слишком больших компьютерных ресурсов. Например, для расчета молекулы небольшого белка цитохром-С (1738 атомов) неэмпирическим методом DFT по специализированной программе ProteinDFT на кластере, содержащем 15 высокопроизводительных микропроцессоров HP Alpha 21264, требуется порядка 24 часов на выполнение одной итерации, а на весь расчет - больше одного месяца, даже без оптимизации геометрии.

Для больших молекулярных систем, содержащих от 10³ до 10⁶ атомов, целесообразно применение полуэмпирических методов квантовой химии в так называемом приближении нулевого дифференциального перекрывания [1], в общем случае имеющих асимптотическую сложность расчета O(N³), где N – размерность задачи, пропорциональная числу атомов. Асимптотическая сложность определяется диагонализацией матриц (решением симметричной проблемы собственных значений) и для сверхбольших молекул неприемлема даже при расчетах на суперЭВМ.

Для расчета физико-химических свойств нужны не сами собственные вектора, а матрица плотности P, являющаяся функцией от них. Численный метод прямого нахождения P - purification (“очистка”)- был разработан еще в 1960 г [2], однако в силу отсутствия в то время необходимых вычислительных ресурсов его применение было ограничено расчетом только небольших молекул. В 90-х гг. ХХ века на основе этого метода были разработаны различные модификации, позволяющие ускорить процесс вычислений. Одной из таких модификаций является метод Пальцера- Манолополиса [3].

Симметричная матрица P является идемпотентной, если P²=P. Мерой идемпотентности может служить величина

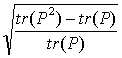, где tr(P) – след матрицы P.

Метод классической “очистки” McWeeny [2] состоит в проведении итерационного процесса по формуле , где P- матрица плотности. Процесс останавливается при достижении заданной точности по идемпотентности. В результате ряда исследований были найдены более быстро сходящиеся методы, являющиеся модификациями метода классической “очистки”. Одним из них является модификация Пальцера-Манолополиса [3]. В этом методе итерационная формула для нахождения матрицы плотности P выглядит следующим образом:

,

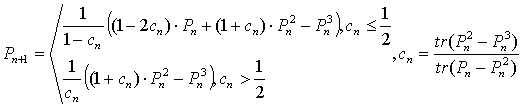где n – номер шага итерационного процесса.

Для повышения эффективности вычислений и учитывая потенциально сверхбольшие размеры матрицы (~10⁶x10⁶ элементов), целесообразно осуществить разбиение матрицы P на блоки и организовать параллельное вычисление блоков на разных процессорах.

В докладе представлены параллельная модификация метода Пальцера-Манолополиса и её реализация на языке Фортран 95 с использованием интерфейса передачи сообщений MPI. В параллельной реализации осуществлено два варианта рассылок – широковещательная рассылка через MPI_Bcast (см. пример на рис.1) и более оптимальная с использованием попарных вызовов MPI_Send/MPI_Recv (см. пример на рис.2).

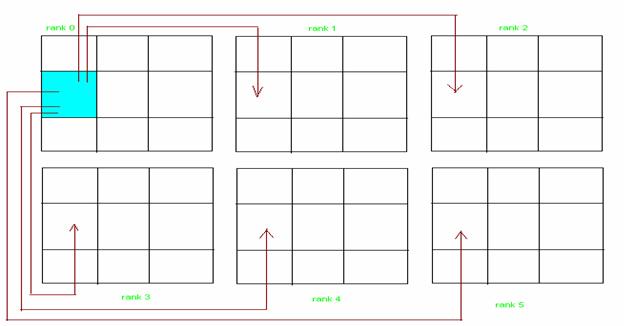
Рис.1. Схема широковещательной рассылки для 6 процессоров (первый процессор рассылает блок остальным пяти).

В случае использования неблокирующихся коммутаторов во 2-ом варианте рассылок возникает дополнительная возможность организовать одновременные пары пересылок, что уменьшает общее время расчета.

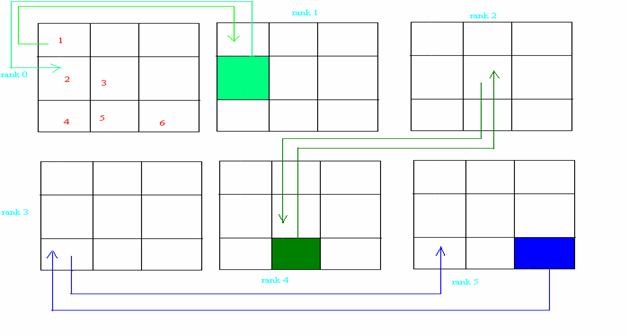
Рис.2 Схема, иллюстрирующая попарные рассылки блоков матрицы.

Тестирование проводилось в кластере на базе процессоров Intel Xeon Pentium 4/2.6 ГГц с использованием коммуникационной технологии Myrinet 2000 (пиковая пропускная способность 250 Мбайт/c). Тестирование программы производилось на молекуле полипептида с размерностью базиса 7500 (около 3000 атомов). Результаты тестирования для двух способов рассылки приведены в таблице 1.

Таблица 1.

Широковещательная рассылка			Рассылка send/receive
Число процессоров	Ускорение	Эффективность	Число процессоров	Ускорение	Эффективность
3	2.59	0.89	3	2.62	0.88
6	4.37	0.73	6	4.60	0.77

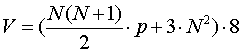Основные затраты по памяти можно оценить по формуле байт – для хранения трех матриц порядка NxN (P, P² и P³ соответственно). Для метода Гоедекера-Коломбо, на основании которого разработана параллельная программа [3] для прямого нахождения матрицы плотности P с применением полиномов Чебышева, затраты по памяти можно оценить как байт, где p – порядок полинома Чебышева. Оценки приведены для расчетов с двойной точностью.

Таким образом, методы очистки предъявляют значительно меньшие требования к памяти, чем метод Гоедекера-Коломбо. Так, для достижения точности 10^-2 уже требуется полином 10-го порядка. Если исходить из требования размещения всей матрицы в памяти узла кластера, то при адресуемом адресном пространства в 2 Гбайт максимально возможная размерность матрицы для расчетов методом Гоедекера-Коломбо составляет порядка 4500х4500, а для методов очистки - порядка 8500х8500.

Авторы выражают благодарность ВЦ имени А.А. Дородницына РАН за возможность использования его кластерных ресурсов для отладки и тестирования программы.

Работа поддержана РФФИ, проект 04-07-90220.

ЛИТЕРАТУРА

1. Степанов Н.Ф. Квантовая механика и квантовая химия. – Изд-ва “Мир” и “МГУ”, М., 2001, 518 с.

2. McWeeny R., Rev. Mod. Phys. 32, 1960, p.335.

3. Бобриков В.В., Чернецов А.М., Шамаева О.Ю. Распараллеливание квантово-химических расчетов матрицы плотности с использованием полиномов Чебышева. Труды международной конференции “Информационнные средства и технологии”, 12-14 октября 2004 г., в 3-х т.т. Т1.-М.: Янус-К, 2004.-С.219-222.

4. Anders M.N. Niklasson, C.J. Tumczak, Matt Challacombe. Trace resetting density matrix purification in O(N) self-consistent-field theory J. of Chemical Physics, v. 118 N 15, 2003, pp 1-10.