РАСПАРАЛЛЕЛИВАНИЕ ЗАДАЧИ РАСЧЕТА НАДЕЖНОСТИ

И.И. Ладыгин, С.Г. Яньков

(Москва, Московский Энергетический Институт (технический университет), Россия)

Процесс решения больших прикладных задач на параллельных вычислительных системах (ВС) [1] представляет собой весьма трудоемкую задачу. Помимо того, что перед началом реализации прикладной задачи необходимо выбрать ВС, на которой она будет выполняться и средство параллельного программирования (СПП), с помощью которого она будет создаваться, программисту необходимо представить свою программу в параллельном виде. Основной целью решения больших задач на параллельных ВС чаще всего является максимально сократить время ее выполнения, по сравнению со временем решения той же программы на однопроцессорной ВС. Для достижения этой цели при разработке программы программисту необходимо учитывать особенности как выбранной ВС, так и выбранной СПП, которые непосредственно влияют на представление задачи в параллельном виде. На сегодняшний момент не существует средств, позволяющих программисту представить свою задачу в параллельном виде, учитывающем особенности выбранных для реализации задачи ВС и СПП. В данной работе предлагается метод распараллеливания прикладных задач для решения их на кластерных системах, который позволяет учитывать основные особенности такой ВС, что в свою очередь позволяет минимизировать время их выполнения. Разработка метода проводилась на примере задачи расчета надежности ВС по интервалам времени [2]. Суть задачи, ее графическое представление и трудности представления в параллельном виде подробно были рассмотрены в [3].

При разработке параллельных программ для кластерных систем необходимо учитывать следующие основные особенности ВС [4]

- способ взаимодействия узлов ВС – передача сообщений;

- необходимость равномерной загрузки всех вычислительных узлов (ВУ) системы;

- возможная неоднородность ВУ.

Рассмотрим более подробно, каким образом можно учесть данные особенности кластерных систем.

Передача сообщений используется для взаимодействия в системе, т.е. для пересылки необходимой информации между ВУ ВС. При этом на время выполнения программы существенное влияние оказывают характеристики коммутационной сети (КС), по которой происходят обмены. Это – латентность и скорость передачи данных [1]. Данные характеристики являются фиксированными и постоянными для конкретной кластерной системы. Поэтому для сокращения общего времени решения задачи необходимо сократить общее время обмена информацией между ВУ, а это возможно только за счет сокращения количества передач в программе. Необходимо отметить, что если две части задачи (ЧЗ) – вершины графа задачи [3] - выполняются на одном ВУ и между ними необходим обмен информацией, то время такого обмена принимается за ноль, так как обмен происходит через локальную память данного ВУ. Таким образом, необходимо распределить ЧЗ таким образом, чтобы минимизировать количество передач между ВУ.

Также время выполнения программы можно сократить за счет сокращения времени простоев (ожидания данных) каждого ВУ. Это можно сделать за счет балансировки загрузки ВУ, учитывая итерационный характер расчета надежности с помощью метода моделирования по интервалам времени. В таком случае время расчета каждым ВУ будет примерно одинаково и передачи можно начинать без задержек.

Неоднородность ВУ системы может заключаться в различных производительностях узлов, в различных операционных системах, установленных в каждом узле, в различных способах представления данных и т.д. При этом на время выполнения задачи наиболее существенно может влиять неоднородность в производительностях ВУ. Для учета данного фактора при балансировке загрузки узлов кластера необходимо брать в расчет реальную производительность каждого узла, т.е. загружать его либо большим количеством операций, либо меньшим по сравнению с другими ВУ.

Таким образом, необходим алгоритм распределения ЧЗ по узлам ВС, учитывающий все перечисленные особенности, т.е. позволяющий равномерно распределить ЧЗ по узлам ВС, обеспечивающий при этом минимальное количество передач между процессорами. Составим математическую модель, отражающую суть задачи распределения. За основу возьмем модель известной «задачи о рюкзаке», в которой необходимо загрузить рюкзак вещами из множества вещей определенной массы и стоимости, чтобы суммарная стоимость загруженных вещей была максимальна, а суммарный вес не превышал заданный. Математическая модель распределения ЧЗ по ВУ кластера описывается формулой 1. Решение данной модели дает матрицу распределения ЧЗ по узлам ВС, «1» в ячейке [i, j] матрицы говорит о том, что ЧЗ i будет выполняться на ВУ j ВС.

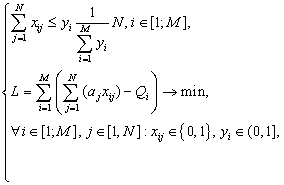(1),

Обозначения: N – общее количество ЧЗ; M – общее количество доступных ВУ системы; x_ij – двоичная переменная, 1 – если j-й узел назначен на i-й ВУ, 0 – в противном случае; a_j – количество связей (передач) j-й ЧЗ; Q_i – количество связей i-го ВУ, время передачи которых можно обнулить; y_i – относительная производительность i-го ВУ.

Пояснения к формуле: В данной модели критерием оптимизации (минимизации) является общее количество передач «ВУ–ВУ». Как уже говорилось, его можно уменьшить за счет распределения ЧЗ по узлам системы, при котором можно сократить (обнулить) максимальное число передач (времен). Общее количество передач в формуле складывается из суммы всех передач за вычетом обнуленных каждой ЧЗ для всех ВУ системы.

Введенные в модели ограничения отвечают за балансировку загрузки ВУ согласно их производительности. Правая часть ограничения представляет собой произведение относительной производительности узла системы на общее количество ЧЗ. Таким образом, определяется максимально возможное количество ЧЗ, назначаемых на данный ВУ. Т.е. каждый процессор должен выполнять объем работ не превосходящий его возможности в производительности.

Составив, таким образом, математическую модель, теперь необходимо ее решить. На сегодняшний момент существует несколько методов оптимизации для решения похожих задач, которые так или иначе можно преобразовать под приведенную модель. Из них можно отметить метод динамического программирования, при котором данную модель можно разбить на множество подмоделей распределения множества ЧЗ на один ВУ. Таких подзадач будет столько, сколько процессоров в рассматриваемой ВС. При этом каждая подзадача сводится к решению задачи о рюкзаке. Также в данном случае можно применить метод ветвей и границ. Но он не гарантирует оптимального результата и в настоящее время почти не применяется. Из современных методов можно отметить генетический алгоритм. Он пока еще плохо разработан и все его реализации достаточно уникальны и не подходят для решения поставленной задачи. В данной работе, для решения описанной модели предлагается алгоритм, построенный на основе известных стратегий назначения [5]. Суть метода заключается в последовательном выборе из множества ЧЗ по определенным правилам конкретной ЧЗ и назначения ее на выбранный по определенным правилам узел ВС. Сначала выбираются ЧЗ с максимальным количеством связей и назначаются на ВУ с минимальным количеством ЧЗ. Когда в оставшемся множестве ЧЗ все ЧЗ будут связаны с уже распределенными, тогда начинают выбираться ЧЗ с максимальным количеством связей с уже распределенными ЧЗ и минимальным количеством связей вообще. Назначение происходит на ВУ, имеющий минимальное количество назначенных ЧЗ и минимальное количество связей.

Предложенный алгоритм распределения ЧЗ по ВУ ВС позволяет разрабатывать параллельные программы, отвечающие особенностям кластерных систем, и дает возможность выполнять прикладные задачи за приемлемое время. При этом время работы алгоритма распределения не велико и оно практически мне влияют на общее время работы программы. В дальнейшем планируется продолжить процесс исследования возможных методов решения поставленной задачи и предложить законченную программную реализацию разработанного метода, которую можно будет использовать при решении широкого круга прикладных задач.

ЛИТЕРАТУРА

1. Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ-Петербург, 2002. – 608 с.: ил.

2. Ладыгин И.И., Калинина Г.А. Исследование надежности вычислительных систем. Описание лабораторных работ по курсу «Основы теории надежности».–М.: Издательство МЭИ,1999.–32с.

3. Доклады международной конференции «Информационные средства и технологии», Ладыгин И.И., Яньков С.Г. «Решение задачи анализа надежности на параллельной вычислительной системе», сс. 140-143, том 3, 2003.

4. Интернет-сайт http://www.citforum.ru/

5. Ладыгин И.И., Калинина Г.А. Лабораторные работы по курсу «Вычислительные системы».–М.: Издательство МЭИ,1999.–32с.