Проблема византийских генералов

В основе модели системы взаимных проверок лежит принцип распределенного ядра. Согласно данному принципу диагностическое ядро системы заранее неизвестно и определяется на основе результатов взаимных проверок: в него включаются учащиеся, правильно ответившие на вопрос и правильно оценившие другие ответы (надежные учащиеся) [1,2,3].

Система работает следующим образом. Всем учащимся выдается одинаковая тестовая задача, каждый решает ее и передает посредством телекоммуникаций свое решение некоторому множеству абонентов (учащихся) для оценки, состав адресатов может меняться и заранее неизвестен посылающему [2]. Графически данная система представляется в виде орграфа O = (V,E), где V = {v₁ , v₂ , ... , v_n} – множество учащихся, a E - множество дуг, указывающих на логические взаимосвязи между ними. Оценка a_ij ответов происходит по двухбалльной шкале (зачет-незачет): a_ij = 1, если абонент v_iопределяет ответ абонента v_jкак неправильный, и a_ij = 0 в противном случае. При этом считается, что если v_i Î G, где G - множество хорошо подготовленных учащихся, то оценка (симптом) a_ij является надежной, в противном случае, v_i Î F (F - множество неподготовленных учащихся), оценка a_ij - ненадежна (ПМЧ-модель). Совокупность всех симптомов a_ij образует синдром A=< a_ij >. В графовой модели неподготовленные учащиеся интерпретируются как дефектные вершины.

Особенность использования этой модели для проверки знаний состоит в субъективизме взаимных оценок (в отличие от технических систем), что приводит к своеобразным ошибкам, которые получили название враждебных (byzantine) или проблемы византийских генералов.

В дальнейшем, будем называть вершину, которая соответствует учащемуся, неправильно решившему свою тестовую задачу, неисправной, а вершину, которая соответствует учащемуся, правильно решившему свою тестовую задачу, но неправильно оценившему ответы других учащихся, враждебной. Совокупность неисправных и/или враждебных вершин назовём ненадёжными вершинами (учащимися).

В задаче византийских генералов армия зелёных находится в долине, а n синих генералов возглавляют свои армии, расположенные в горах. Связь осуществляется по надёжным коммуникациям, но из n генералов m являются предателями. Согласие заключается в том, что каждый генерал из n знает, сколько воинов находится под его командой. Ставится цель, чтобы все лояльные генералы узнали численности солдат лояльных армий, т.е. каждый из них получил один и тот же вектор длины n, в котором i-ый элемент либо содержит численность i-ой армии (если её командир лоялен) либо не определён (если командир – предатель) [4,5].

Подобная задача была исследована в 1982 году в [4,5] и соответствующий алгоритм её решения состоит в следующем.

Шаг 1. Каждый генерал посылает всем остальным сообщение, в котором указывает численность своей армии. Лояльные генералы указывают истинное количество, а предатели могут указывать различные числа в разных сообщениях. Генерал g₁ указал 1 (одна тысяча воинов), генерал g₂указал 2, генерал g₃ указал трем остальным генералам соответственно x,y,z, а генерал g₄ указал 4.

Шаг 2. Каждый генерал формирует свой вектор из имеющейся информации, полученной от других генералов.

Получается: vect1 (1,2,x,4), vect2 (1,2,y,4), vect3 (1,2,3,4), vect4 (1,2,z,4)

Шаг 3. Каждый посылает свой вектор всем остальным (генерал g₃ посылает опять произвольные значения).

Генералы (g_i) получают следующие векторы:

g₁	g₂	g₃	g₄
(1,2,y,4)	(1,2,x,4)	(1,2,x,4)	(1,2,x,4)
(a,b,c,d)	(e,f,g,h)	(1,2,y,4)	(1,2,y,4)
(1,2,z,4)	(1,2,z,4)	(1,2,z,4)	(i,j,k,l)

Шаг 4. Каждый генерал проверяет каждый элемент во всех полученных векторах. Если какое-то значение совпадает по меньшей мере в двух векторах, то оно помещается в результирующий вектор, иначе соответствующий элемент результирующего вектора помечается как «неизвестен». Все лояльные генералы получают один вектор (1,2,неизвестно,4) – согласие достигнуто.

Стоит отметить, что для n = 3 и m = 1 согласие достигнуто не будет.

В системе взаимной проверки знаний проблема византийских генералов возникает в случае, когда учащийся дал верный ответ на своё задание, а при проверке других обучаемых, оценки поставил произвольно. Эта вершина (учащийся) является враждебной. Такая ситуация может привести к неправильной расшифровке синдрома.

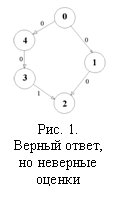На рисунке 1 приведён случай, когда учащийся дал верный ответ на своё задание, но при проверке других обучаемых, поставил произвольные оценки. Все учащиеся правильно решили тестовую задачу, но оценка a₃₂ = 1 неверна. Следовательно, при расшифровке синдрома получается, что учащийся 0 – ненадёжен (согласно утверждению из [2]). Такой результат расшифровки не является достоверным.

Данная ситуация может возникнуть в результате следующих причин:

1. Механическая ошибка (ввод оценки по ошибке);

2. Умышленное выставление неверной оценки (например, по договорённости);

3. Неправильная оценка ответа (может возникнуть в случае, когда знаний проверяющего учащегося не хватает для выставления верной оценки).

Снизить вероятность возникновения механической ошибки в выставлении оценки можно техническими средствами, например, подтверждение оценки.

Снизить вероятность умышленного выставления неверной оценки можно разъяснением ответственности за неправильную оценку, так как учащийся неверно поставивший оценку, рассматривается как ненадёжный [2]. Для выявления ситуации умышленного выставления неверной оценки перед началом проверки решений учащихся система может отсылать всем одно тестовое задание (с решением), которое она будет брать из своей базы данных (БД) и, следовательно, знать, какое (верное или неверное) решение было отослано учащемуся. Тогда, те учащиеся, которые неправильно оценят решение этого задания, сразу будут исключены из дальнейшей процедуры проверки решений других учащихся. Также можно предусмотреть в системе контроль времени проверки учащимся ответов других учащихся. Например, если проверка была очень быстрой, то эту вершину можно считать подозрительной.

Неправильная оценка ответа надёжным учащимся маловероятна, если исходить из структуры деятельности человека, где на первом уровне находится узнавание объектов, свойств, процессов данной области, а на втором (более высоком) – воспроизведение информации, операций, действий Для сведения к минимуму возможности появления такой ситуации можно учащемуся во время проверки ответов предоставлять подробную методику проверки ответа, либо правильный ответ.

Несмотря на то, что вероятность возникновения данной ситуации можно с помощью приведённых выше мероприятий свести к минимуму, она возможна. Поэтому в системе нужно предусмотреть возможность отслеживать рассмотренную критическую ситуацию.

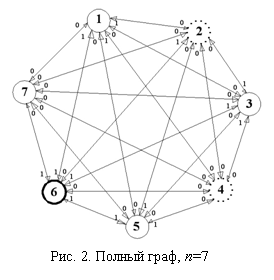Рассмотрим граф системы для n = 7 (рис. 2, где изображены двусторонние стрелки). В данной системе вершины 2 и 4 являются враждебными, вершина 6 – неисправна. Для расшифровки синдрома системы усовершенствуем алгоритм, предложенный в [5]. Для его реализации в системе нужно организовать тестовые связи каждый с каждым (полный граф).

АЛГОРИТМ МП

Шаг 1. Для каждой вершины (учащегося) составляется вектор оценок, где каждый элемент равен оценке (0 или 1), поставленной проверяемому учащемуся. Сам себе оценку учащийся поставить не может, поэтому на месте этого элемента ставится прочерк (-). После составления векторов для всех учащихся получаем матрицу размерностью n x n (табл. 1).

Шаг 2. Нахождение результирующего вектора. Просматривается каждый столбец матрицы элемент за элементом в поисках оценки, которая была проставлена наибольшим числом учащихся (мажоритарный принцип). Если такая оценка была найдена, то она заносится в результирующий вектор и будет учитываться при дальнейшем выявлении неисправных и/или враждебных вершин. Иначе, эта оценка не учитывается.

Для графа, изображённого на рисунке 2 получим результирующий вектор: (неизвестно,0,неизвестно,0,неизвестно,1,неизвестно).

Шаг 3. Сравнение результирующего вектора с каждой строкой матрицы. Если все элементы результирующего вектора совпадают с элементами строки, значит учащийся, которому соответствует эта строка, признаётся надёжным и ставится знак “+”. Если хотя бы один элемент результирующего вектора не совпал со соответствующим элементом строки, то учащийся признаётся ненадёжным и ставится знак “-“ (табл. 1). В результате выяснили, что ненадёжными являются 2, 4 и 6 вершины.

Шаг 4. Выяснение, является ли вершина со знаком “-“ (ненадёжная вершина)враждебной или неисправной. Для этого определяем, чему врезультирующем векторе равен элемент (0 или 1), стоящий на месте

выявленной на Шаге 3 неисправной вершины. Если стоит 0, значит эта

Таблица 1
Кто проверяет	Кого проверяет							Результат сравнения с результирующим вектором
	1	2	3	4	5	6	7
1	-	0	0	0	0	1	0	+
2	1	-	1	0	1	0	1	-
3	0	0	-	0	0	1	0	+
4	1	0	1	-	1	0	1	-
5	0	0	0	0	-	1	0	+
6	1	1	1	0	1	-	1	-
7	0	0	0	0	0	1	-	+

вершина является враждебной, если 1 – вершина неисправна.

Так как на Шаге 3 было выяснено, что ненадёжными являются вершины 2, 4 и 6, то выясняем в результирующем векторе, чему равны элементы на этих местах. Они равны соответственно 0, 0, 1. Отсюда следует, что вершины 2 и 4 являются враждебными, а вершина 6 – неисправной.

Вывод: данный алгоритм лучше применять для небольших групп с n9. Иначе, будет очень большая нагрузка на каждого учащегося.

На практике не всегда результирующий вектор содержит неизвестные значения. Например, он может принимать вид (0,0,0,0,0,0,0). Такой вектор может получиться при наличие в системе трёх враждебных вершин. Тем не менее приведённый алгоритм однозначно и правильно их выявляет.

Утверждение.

В полном графе системы взаимной проверки знаний с числом вершин (учащихся), равным n и числом неисправных и/или враждебных вершин (учащихся), равным t [(n-1)/2], возможно однозначное и правильное определение состояния вершин без подключения арбитра.

Доказательство:

На основании теоремы, доказанной в для технических систем, для однозначной расшифровки число исправных вершин должно быть больше половины, то есть применительно к системе взаимной проверки знаний число надёжных учащихся должно быть равно n-[(n-1)/2]. Согласно алгоритму, в результирующий вектор попадает оценка, поставленная большинством (мажоритарный принцип), а большинство в полном графе будут составлять надёжные учащиеся, которые верно оценивают другие вершины.

Следовательно, однозначно и правильно будут выявлены все неисправные и/или враждебные вершины без подключения арбитра, если их число не превышает n-(n-[(n-1)/2]) = [(n-1)/2].

Следствие.

В случае, если t > [(n-1)/2], нужно подключать арбитра.

В заключение отметим, что априорно неизвестно число ненадёжных учащихся, поэтому для контроля следует подключать арбитра на любого учащегося, который был признан подготовленным.

ЛИТЕРАТУРА

1. Афонин В.А., Ладыгин И.И. Построение отказоустойчивых вычислительных систем. – М.: МЭИ, 1987. – 68 с.

2. Афонин В.А., Смолко А.В., Лунгулло С.В. Архитектура системы взаимной проверки знаний // Международный форум информатизации МФИ-97. Доклады международной конференции “Информационные средства и технологии”, т.3.-М.: Изд-во “Станкин”, 1997.-С.79-84.

3. Афонин В.А., Свиридов А.П., Смолко А.В. О новом классе компьютерных систем для группового обучения с арбитром // Информационные технологии, 1997, №8, С.44-46.

4. Крюков В.А. Распределённые системы.-Курс лекций // Лаборатория параллельных информационных технологий. НИВЦ МГУ.

5. Lamport L., Shostak R., Pease M. The Byzantine Generals Problem // ACM Transactions on Programming Languages and Systems, Vol. 4, No. 3, July 1982, Pages 382-401.