Система взаимной проверки знаний
с арбитром предназначена для контроля уровня подготовки группы учащихся. Взаимная проверка состоит в оценивании ответа
отдельного учащегося несколькими его коллегами [2]. В [3] рассмотрена проблема византийских
генералов, возникновение которой возможно в данной системе, и изложен алгоритм
нахождения враждебных (byzantine) вершин. В данной статье предлагается алгоритм для
оптимальной графовой модели Dd,t [4], а затем рассматривается возможное сочетание с
алгоритмом из [3].
Рассмотрим ситуацию, когда
подготовленный учащийся, правильно ответивший на поставленный вопрос,
ошибочно или по договоренности ставит не соответствующую оценку на проверяемый
им ответ (например, ставит оценку “правильно” при проверке неверного ответа
(ответа ненадежного студента)). Данная
ситуация с числом учащихся n=5 представлена на рисунке 1. Система 2-диагностируемая. Количество тестовых связей nt – оптимальная система с минимальным
числом дуг в графе, где n – количество вершин (учащихся) в
системе; t – показатель, равный максимальному числу вершин,
принадлежащих множеству F (где
F – множество ненадёжных вершин), при
котором возможна однозначная и правильная расшифровка синдрома A [1].
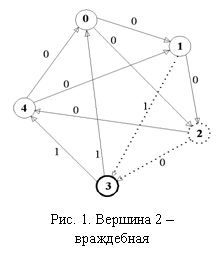 Здесь 3vF, а учащийся 2, признанный надёжным – говорит,
что 3vG, что неверно (где G – множество надёжных учащихся). Таким образом, общий результат расшифровки
будет неверным: несложно заметить, что в
системе присутствует нулевой контур 0-1-2-4.
Следовательно, вершины 0,1,2,4vG.
Но вершина 2 говорит, что вершина 3vG, в то время как вершина 1 говорит,
что 3vF.
В этом случае возникает противоречие, поэтому требуется подключить
арбитра для выяснения состояния вершины 3.
Пусть, после проверки арбитром, 3vF.
Тогда все вершины контура 0-1-2-4vF.
То же будет и в случае, если после проверки арбитра, он признает 3vG.
Здесь 3vF, а учащийся 2, признанный надёжным – говорит,
что 3vG, что неверно (где G – множество надёжных учащихся). Таким образом, общий результат расшифровки
будет неверным: несложно заметить, что в
системе присутствует нулевой контур 0-1-2-4.
Следовательно, вершины 0,1,2,4vG.
Но вершина 2 говорит, что вершина 3vG, в то время как вершина 1 говорит,
что 3vF.
В этом случае возникает противоречие, поэтому требуется подключить
арбитра для выяснения состояния вершины 3.
Пусть, после проверки арбитром, 3vF.
Тогда все вершины контура 0-1-2-4vF.
То же будет и в случае, если после проверки арбитра, он признает 3vG.
Вывод: t=2, а число ненадёжных вершин
(учащихся) после расшифровки больше, что неверно. Следовательно, нужно находить характерные
синдромы. В примере – это тестовые связи,
изображённые пунктирной линией. В случае
нахождения такого синдрома предлагается использовать следующий алгоритм.
АЛГОРИТМ НОУ
Шаг 1. Подключение арбитра в случае возникновения
противоречия (например: 1 говорит, что 3vF, а
2-ой – что 3vG, при этом 1,2 принадлежат нулевому
контуру), на подозрительную вершину (в нашем случае – 3) для выяснения её
состояния (исправна или неисправна)
 Шаг 2. Арбитр проверяет какую-то из вершин, которые тестируют
подозрительную вершину (вершина 3) и
признаны надёжными (vG), (т.е. вершину 1 или 2) в зависимости от того, каким
был результат проверки арбитром вершины 3 (если 3vF, то арбитр проверяет вершину 2; если
3vG, то
арбитр проверяет вершину 1). Если проверенная
вершина (1 или 2) оказалась надёжной (vG), следовательно, это вражеская
вершина и при дальнейшей расшифровке она не используется. На рисунке 4, арбитр проверит вначале вершину
3 (vF), а потом проверит вершину 2vG, следовательно
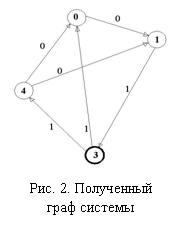
2-ой учащийся не будет дальше участвовать в расшифровке. После этого, граф системы будет выглядеть,
как показано на рисунке 2.
Шаг 2. Арбитр проверяет какую-то из вершин, которые тестируют
подозрительную вершину (вершина 3) и
признаны надёжными (vG), (т.е. вершину 1 или 2) в зависимости от того, каким
был результат проверки арбитром вершины 3 (если 3vF, то арбитр проверяет вершину 2; если
3vG, то
арбитр проверяет вершину 1). Если проверенная
вершина (1 или 2) оказалась надёжной (vG), следовательно, это вражеская
вершина и при дальнейшей расшифровке она не используется. На рисунке 4, арбитр проверит вначале вершину
3 (vF), а потом проверит вершину 2vG, следовательно
2-ой учащийся не будет дальше участвовать в расшифровке. После этого, граф системы будет выглядеть,
как показано на рисунке 2.
Шаг 3. Используем алгоритм расшифровки синдрома для полученного графа [1]. В результате получим, что 0,1,4vG, 3vF.
Покажем, как можно совместно
использовать АЛГОРИТМ НОУ и АЛГОРИТМ МП, рассмотренный в [3], в оптимальной
системе с числом тестовых связей nt.
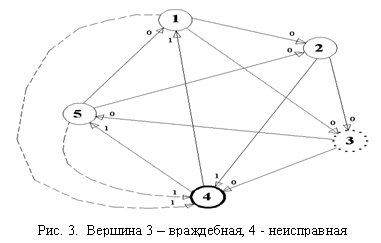
На рисунке 3 представлен граф cистемы взаимной проверки знаний с числом
учащихся, равным 5.
Вершина 3 – враждебная, а вершина
4 – неисправная.
|
Таблица 1 |
|||||
|
Кто проверяет |
Кого проверяет |
||||
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
- |
- |
- |
1 |
- |
|
2 |
- |
- |
- |
1 |
- |
|
3 |
- |
- |
- |
0 |
- |
|
4 |
- |
- |
- |
- |
- |
|
5 |
- |
- |
- |
1 |
- |
Вершины 1-2-3- 5
образуют нулевой контур. Согласно АЛГОРИТМУ НОУ, учащегося 4 должен
проверить арбитр, потому что 2 говорит, что он
ненадёжен (ставит “1”), а 3 говорит, что надёжен (ставит “0”), хотя и учащийся
2, и учащийся 3 принадлежат нулевому контуру.
Чтобы не подключать арбитра, нужно подключить дополнительные тестовые
связи для проверки 4-го учащегося. На
рисунке 3 – это пунктирные стрелки.
Используем АЛГОРИТМ МП (табл. 1). По мажоритарному принципу для
учащегося 4 получаем “1”, то есть вершина 4 неисправна, а согласно АЛГОРИТМУ НОУ
вершина 3 является враждебной, так как говорит, что вершина 4 исправна.
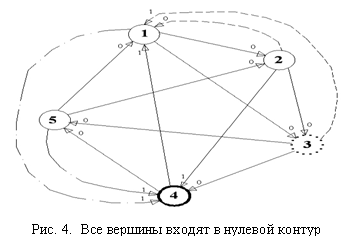
Рассмотрим теперь случай,
когда все вершины графа принадлежат нулевому контуру (рис. 4). Как будет показано ниже, вершина 4 –
неисправна, вершина 3 – враждебна.
Вершины 1-2-3-4-5 образуют
нулевой контур. Но между этими вершинами
есть единичные дуги (a24 и
a41). В технической диагностике в этом случае все
вершины контура были бы признаны ненадёжными.
Но при возможности появления в системе враждебных вершин такой вывод
сразу делать нельзя.
В приведённом графе
состояние вершин 1 и 4 неизвестно (на основании АЛГОРИТМА НОУ). Подключим вначале к вершине 1 дополнительные
тестовые связи (на рис. 4 – пунктирные стрелки). Применим АЛГОРИТМ МП (табл. 2). По мажоритарному принципу получается
неопределённость (a21 = a51 = 0; a31 = a41
= 1, где aij - симптом графа). Подключим дополнительные тестовые связи к
вершине 4 (рис. 4). По мажоритарному
принципу получаем “1”, то есть вершина 4 – неисправна (табл. 3). Тогда, согласно АЛГОРИТМУ НОУ, вершина 3 –
враждебная.
В результате того, что
после подключения дополнительных тестовых связей к вершине 1, враждебная
вершина 3 поставила неправильную оценку (a31
= 1), возникла ситуация неопределённости и состояние вершины 1 определить
не удалось что привело к подключению дополнительных тестовых связей к вершине
4. Поэтому нужно учитывать следующее
эвристическое утверждение.
Утверждение.
В ситуации, когда все
вершины входят в нулевой контур в случае присутствия в системе 2-х (или более) вершин,
чьё состояние не определено (после её проверки одна вершина из нулевого контура
ставит “0”, а другая “1”), вначале для подключения дополнительных тестовых
связей всегда целесообразно выбирать вершину, которая входит в меньшее
количество нулевых контуров.
На рисунке 4 две
неопределённые вершины, но вершина 4 входит в меньшее количество нулевых
контуров. Следовательно, нужно для
подключения дополнительных тестовых связей вначале выбрать её.
|
Таблица 2 |
|||||
|
то проверяет |
Кого проверяет |
||||
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
- |
- |
- |
- |
- |
|
2 |
0 |
- |
- |
- |
- |
|
3 |
1 |
- |
- |
- |
- |
|
4 |
1 |
- |
- |
- |
- |
|
5 |
0 |
- |
- |
- |
- |
|
Таблица 3 |
|||||
|
Кто проверяет |
Кого проверяет |
||||
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
- |
- |
- |
1 |
- |
|
2 |
- |
- |
- |
1 |
- |
|
3 |
- |
- |
- |
0 |
- |
|
4 |
- |
- |
- |
- |
- |
|
5 |
- |
- |
- |
1 |
- |
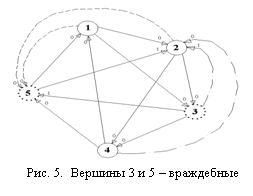 Наконец, рассмотрим систему, в которой
все вершины (учащиеся) входят в нулевой контур, и вершины (учащиеся) 3 и 5
являются враждебными (рис. 5).
Наконец, рассмотрим систему, в которой
все вершины (учащиеся) входят в нулевой контур, и вершины (учащиеся) 3 и 5
являются враждебными (рис. 5).
Вершины 1-2-3-4-5 образуют нулевой
контур. Но состояние вершин (учащихся) 2
и 5 неизвестно из-за наличия входящей единичной дуги. Согласно утверждению, обе вершины входят в
одинаковое количество нулевых контуров. Следовательно, выбор вершины (учащегося) для
подключения дополнительных тестовых связей произволен. Подключим к вершине 5 (табл. 4). По мажоритарному принципу получим “0”, то
есть вершина 5 – исправна. Тогда вершина
3 является враждебной. Теперь
неизвестно, кто обманывает – учащийся 1 или учащийся 5, которые
тестируют учащегося 2. Следовательно,
подключим дополнительные тестовые связи к учащемуся 2 (табл. 5). По мажоритарному принципу получается
неопределённость, но вершина 3 является враждебной, следовательно, результат
проверки a32 учитывать не
нужно. Тогда, по мажоритарному принципу
получается “0” и вершина 2 исправна.
Отсюда следует, что вершина 5 – враждебная.
|
Таблица 4 |
|||||
|
Кто проверяет |
Кого проверяет |
||||
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
- |
- |
- |
- |
0 |
|
2 |
- |
- |
- |
- |
0 |
|
3 |
- |
- |
- |
- |
1 |
|
4 |
- |
- |
- |
- |
0 |
|
5 |
- |
- |
- |
- |
- |
|
Таблица 5 |
|||||
|
Кто проверяет |
Кого проверяет |
||||
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
- |
0 |
- |
- |
- |
|
2 |
- |
- |
- |
- |
- |
|
3 |
- |
1 |
- |
- |
- |
|
4 |
- |
0 |
- |
- |
- |
|
5 |
- |
1 |
- |
- |
- |
В заключение отметим важность
реализации проверки таким образом, чтобы учащийся до завершения взаимного
диагностирования не мог узнать, признан он подготовленным или нет.
Для решения этой задачи
реализация системы должна быть построена на следующих принципах: результаты входного контроля являются
внутренней информацией системы и не показываются учащемуся ни во время, ни
после диагностирования; каждое последующее решение на проверку отсылается
учащемуся только после того, как он проверил предыдущее; очередное решение на
проверку выбирается случайно из числа решений, ожидающих проверки данным
учащимся.
Рассмотренная в данной
статье и в статье [3] методика позволяет локализовать неисправные и/или
враждебные вершины с уменьшением числа подключений арбитра для оптимальной
системы Dd,t.
ЛИТЕРАТУРА
1. Афонин В.А., Ладыгин
И.И. Построение отказоустойчивых вычислительных систем. – М.: МЭИ, 1987. – 68
с.
2. Афонин В.А., Смолко
А.В., Лунгулло С.В. Архитектура системы взаимной
проверки знаний // Международный форум информатизации МФИ-97. Доклады международной конференции
“Информационные средства и технологии”, т.3.-М.: Изд-во “Станкин”,
1997.-С.79-84.
3. Афонин В.А., Пудов В.А. Проблема
византийских генералов при расшифровке синдрома в системе взаимной проверки
знаний с арбитром // Международный форум информатизации МФИ-05 (в данном
сборнике).
4. Димитриев Ю.К. Самодиагностика модульных
вычислительных систем.-Новосибирск: ВО “Наука”. Сибирская издательская фирма, 1993.-293с.