ОБ ИЗДЕРЖКАХ ДВОЙНОГО ХЕШИРОВАНИЯ
ПРИ ПОИСКЕ ДАННЫХ
И.В.Шевченко
(Москва, Московский энергетический
институт (ТУ), Российская Федерация)
Двойное хеширование всюду рассматривается как благо, призванное сгладить
известные недостатки
хеширования по методу прямой адресации [1]. Усомнимся в этой его роли, но
прежде изучим процессы, протекающие в памяти при хешировании по принципу линейного
опробования и при двойном хешировании.
При отображении записи в таблицу (по ключу записи) в быстрый кэш
вызывается некоторый фрагмент таблицы,
обозначенный хеш-адресом. Размер
фрагмента определяется длиной линии кэша. Если по хеш-адресу искомого ключа
нет, пробуется ключ в соседней позиции и т.д., пока не будет найден ключ или обнаружено его отсутствие в таблице. При малом
размере элемента таблицы в кэш попадает
сразу несколько соседних ее элементов, опробование их ключей выполняется в кэше, т.е. весьма оперативно, и только в случае
неопределенного результата в кэш вызывается соседний фрагмент таблицы для
продолжения поиска ключа.
При слабо заполненной таблице для поиска ключа бывает достаточно
вызова одного фрагмента, но если коэффициент
a ее заполнения высок,
все зависит от компактности элемента таблицы. Если это запись большой длины R,
одной из них достаточно, чтобы загрузить весь быстрый кэш (или большую его часть), и
каждое опробование нового ключа будет приводить к перезагрузке кэша. В таком
случае говорят о промахе мимо кэша [2], подразумевая обращение к памяти за его
пределами. Поэтому при использовании не слишком длинных ключей целесообразно
разделить таблицу на две (рис. 1).
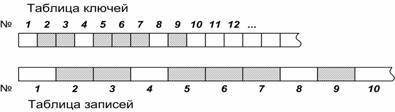
Рис. 1
Поиск (в таблице ключей) идет с минимальным числом промахов мимо кэша.
Если ключ
не найден, он вносится в свободную позицию, а запись - в соответствующую позицию массива записей (режим поиска со вставкой).
Если ключ найден, происходит одно обращение к
«рыхлому» массиву записей или файлу записей. На рис. 2 показано, как растет удельное число
промахов в неразделенной таблице с увеличением длины R записи.
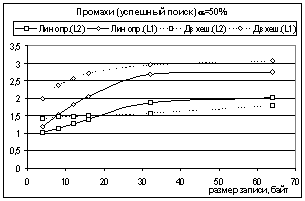
Рис. 2
На рис. 2, 5 обозначение L1
относится к кэшу 1 уровня (быстрому),
L2 – к кэшу 2 уровня (медленному). «Лин опр» обозначает алгоритм линейного опробования,
«Дв хеш» - алгоритм с двойным хешированием.
В таблицах нежелательны длинные ключи и
ссылки на
записи. Соответствие ключа и записи осуществляется по общему их номеру. Итак, таблица ключей должна
быть компактной, что ведет к сокращению числа промахов мимо кэша.
Обратимся теперь к двойному хешированию. Оно чревато промахами мимо кэша
по самой своей природе, ибо
каждое новое опробование ключа происходит в «случайно» выбранной позиции
таблицы*. Поэтому выигрыш в длине поиска,
показанный на рис. 3, может быть перечеркнут
потерями времени из-за промахов мимо кэша. Здесь и ниже любая величина, в
обозначении которой участвует «усп» («неусп»),
будет соответствовать случаю успешного (неуспешного) поиска.
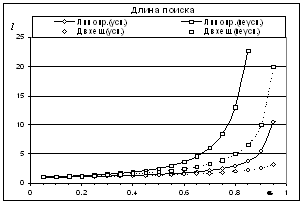
Рис. 3
Оценим соотношение числа промахов при линейном опробовании и двойном
хешировании в компактной таблице в зависимости от коэффициента заполнения
таблицы. Пусть T – размер хеш-таблицы в байтах. Оценим
сначала среднее количество затрагиваемых линий кэша при поиске линейным
опробованием.
Лемма 1. Обозначим через k число записей в
одной линии кэша, а среднюю длину поиска при линейном опробовании – через l. Тогда среднее число
затрагиваемых линий кэша ![]() .
.
Предполагая, что каждое обращение к кэшируемому блоку памяти вызывает
один промах (грубое предположение, приближенно справедливое при T ® ¥), а также, учитывая,
что средняя длина поиска при линейном опробовании равна ![]() ,
, ![]() , имеем следующую лемму.
, имеем следующую лемму.
Лемма 2. Среднее число
промахов при поиске в хеш-таблице с линейным опробованием равно ![]() ,
, ![]() .
.
Для двойного хеширования в предположении, что каждое опробование
вызывает один промах, справедлива аналогичная лемма.
Лемма 3. Среднее число
промахов при поиске в хеш-таблице с двойным хешированием равно ![]() ,
, ![]() .
.
Таким образом, для различных значений параметра k
> 1 можно определить предельное значение aкр заполнения таблицы, при котором линейное опробование
начинает вызывать большее число промахов, чем двойное хеширование. Это значение
достаточно велико.
Так считая типичным размер линии кэша в 32 байта, а размер записи в 4,
8, 16 байтов получаем следующие значения aкр:
|
k |
Успешный поиск |
Неуспешный поиск |
|
8 |
0,98 |
0,94 |
|
4 |
0,95 |
0,86 |
|
2 |
0,81 |
0,67 |
Полученные оценки хорошо
согласуются с результатами экспериментов и позволяют достаточно точно
определять диапазон заполнения таблицы, при котором линейное опробование
быстрее двойного хеширования.
Например, при целом ключе (элемент таблицы имеет длину 4 байта, размер
линии кэша 32 байта) хеширование с линейным исследованием выигрывает по времени у
двойного хеширования вплоть до a = 95% включительно. Эксперименты с таблицами разного размера
(существенно большего, чем размер кэша) подтверждают эти результаты на широком
диапазоне мощностей задач. При большем заполнении таблицы хеширование по методу открытой
адресации вряд ли стоит использовать, как впрочем, и хеширование вообще.
Аналогичная картина имеет место и при целом ключе длиной 8 байтов или при ключе
вещественного типа. На рис. 4, 5 приведены графики зависимости времени поиска и
промахов при неуспешном поиске от коэффициента a заполнения таблицы.
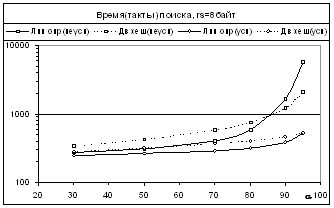
Рис. 4
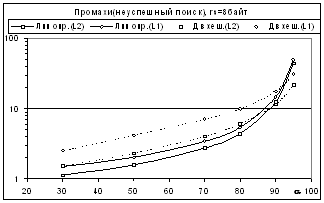
Рис. 5
Видно, что паритет достигается только при более чем 85% заполнении для
неуспешного поиска и более чем 95% заполнении для поиска успешного. Таким
образом, двойному хешированию в
рационально организованных таблицах (см. выше) практически не остается
места применения при числовых ключах. Это следовало бы иметь в виду авторам,
восхваляющим двойное хеширование [3,4]; его критики в публикациях нет.
Единственным полем его применения остаются только символьные и другие длинные
ключи с длиной, сопоставимой (и большей) с размерами линии кэша ЭВМ.
Эксперименты проводились на ЭВМ, с 256 Мб оперативной памяти и
процессором Intel Pentium III 800 МГц. Размер
кэш-памяти первого уровня (L1) 32 Кб, второго
уровня (L2) – 256 Кб.
Программы алгоритмов реализованы как на языке Object Pascal, так и на C++.
Во всех случаях их опробования получены идентичные результаты,
свидетельствующие об их общности.
ЛИТЕРАТУРА
1. Кнут Д. Э. Искусство программирования, том 3.
Сортировка и поиск, 2-е изд.: Пер. с англ. : Уч. пос. – М.: Издательский дом
“Вильямс”, 2000.
2. Зубов В.С., Шевченко И.В. Структуры и методы обработки
данных: Практикум в среде Delphi – M.: Информационно-издательский дом “Филинъ”, 2004.
3.
Седжвик Р.
Фундаментальные алгоритмы на C. Части 1-4. Анализ. Структуры данных.
Сортировка. Поиск. СПб: ООО «ДиаСофтЮП», 2003.
4.
Бакнелл Дж. М.
Фундаментальные алгоритмы и структуры данных в Delphi. СПб: ООО «ДиаСофтЮП»,
2003.