ИНЖЕНЕРНАЯ ФОРМУЛА ДЛЯ РАСЧЕТА ВЕРОЯТНОСТИ СТОЛКНОВЕНИЯ КАДРОВ В СЕГМЕНТЕ ETHERNET

Л.И. Абросимов, Н.А. Соболева

(г. Москва, Московский энергетический институт (Технический Университет) Россия)

Cегменты Ethernet успешно используются в корпоративных вычислительных сетях (КВС) и совместно с новейшими быстродействующими коммуникационными устройствами обеспечивают доступ рабочих станций пользователей к сетевым информационным ресурсам. Рост трафика пользователей и повышение требований к качеству обслуживания приводит к необходимости количественно оценивать производительность сегментов КВС, поэтому разработка математических моделей, количественно оценивающих вероятностно-временные характеристики функционирования КВС, является актуальной.

В качестве модели сегмента Ethernet в соответствии с методом контуров [2] можно использовать одноканальную СМО с неограниченной очередью (см. рис. 1), которая характеризуется: интенсивностью полезного входного потока транзакций, интенсивностью обслуживания в сегменте, интенсивностью фактического потока транзакций в сегменте, и вероятностью столкновений транзакций в сегменте.

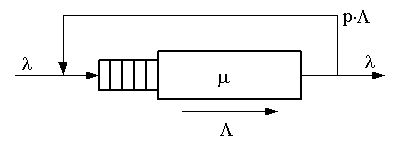
Рис. 1 – Модель сегмента Ethernet

Для модели сегмента в соответствии с формулой Литтла [2] время пребывания в сегменте (с учетом ожидания) определяется соотношением:

(1)

В соотношении (1) n – количество транзакций в сегменте (с учетом ожидания) и для СМО M/M/1/ (2)

Интенсивность зависит от и , а именно: (3)

Следовательно, чтобы определить t и необходимо знать вероятностью столкновений транзакций в сегменте.

Для исследования протокола CSMA/CD и определения р была разработана имитационная модель [1]. Установлено, что вероятность столкновений транзакций в сегменте зависит от числа N станций, длины L пакетов, интенсивности , скорости С передачи в сегменте, времени Т моделирования, длины сегмента.

Разработанная имитационная модель позволяет определить взаимосвязь перечисленных параметров в различных комбинациях и построить график зависимости вероятности р столкновения от интенсивности транзакций в сегменте.[1]

Применение для инженерного проектирования разработанной модели ограничено тем, что для каждого набора параметров приходится выполнять полный цикл моделирования. Для задач проектирования более целесообразно использовать удобные аналитические зависимости (1),(2),(3), полученные для установившегося режима, но для этого необходимо иметь аналитическое соотношение, которое позволяет вычислять вероятность р столкновения по известным параметрам: N, L, , С, .

Попытки получить аналитическое выражение для вычисления р, зависящее от всех перечисленных параметров, привели к громоздкому аналитическому выражению, которое не может быть использовано для инженерных расчетов [1, 4].

В результате проведенного анализа функционирования исследуемого сегмента установлено, что в качестве интегрального параметра, функционально связанного с параметрами N, L, , С, , следует использовать коэффициент полезной загрузки сегмента, который связан аналитическими зависимостями с этими параметрами [3]:

; (4) (5) (6)

Следовательно, задача исследований состоит в том, чтобы, используя имитационную модель сегмента, получить -- графическую зависимость вероятности р столкновения от , а затем аппроксимировать ее адекватным аналитическим соотношением.

С использованием имитационной модели получена зависимость , представленная в виде графика зависимости вероятности р столкновения от коэффициента r загрузки (рис. 2).

Учитывая особенности кривой, предлагается использовать аппроксимирующую функцию вида:

(7)

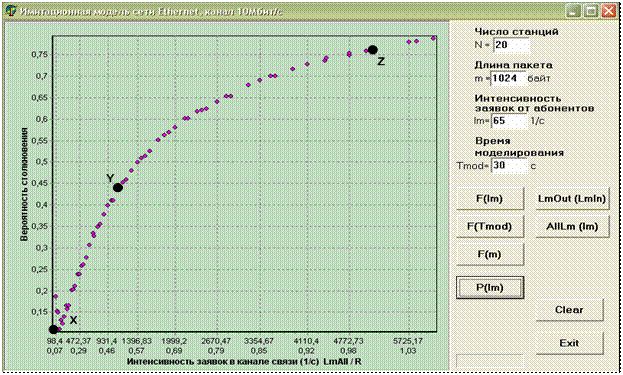
Рис. 2 – График зависимости вероятности р столкновения от и .

Функция (7) имеет масштабирующие коэффициенты: x, y, z, учитывающие специфику аппроксимирующей зависимости. Чтобы найти значения 3-х масштабирующих коэффициентов, выбираем на интервале

r = 0 – 1 три значения р для r= 0; r=0,5; r=1,0, которые соответствуют на рис.2 точкам: X, Y, Z. Они соответствуют значениям вероятности р столкновения – 0, 0.44, 0.77.

В результате получим систему уравнений:

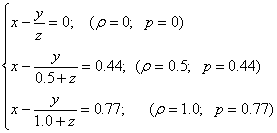(8)

Решением системы уравнений (8) является :x = 3.08 y = 9.24 z = 3

Аппроксимирующая функция, выражающая зависимость вероятности р столкновения от коэффициента r загрузки имеет следующий вид:

(9)

График зависимости вероятности столкновения от коэффициента загрузки и аппроксимирующая кривая представлены на рисунке 3.

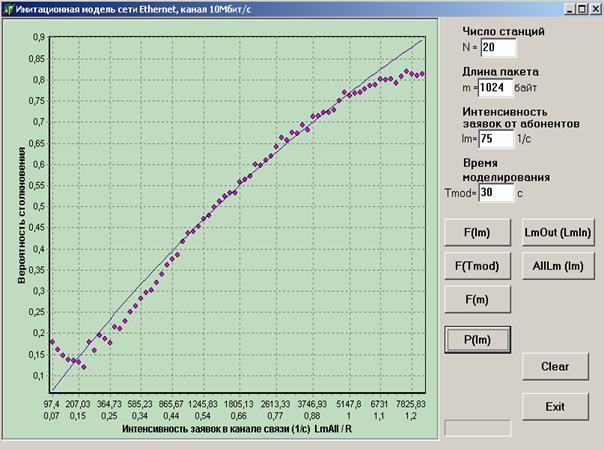
Рис. 3 – График зависимости вероятности р столкновения от коэффициента загрузки и интенсивности полезного входного потока транзакций

Литература

1. Абросимов Л.И., Соболева Н.А. Исследование фрагмента Ethernet методами имитационного и аналитического моделирования. Электронный журнал ВЫЧИСЛИТЕЛЬНЫЕ СЕТИ. Теория и практика, 2004, №1 (4), раздел 10, статья 3. http://network-journal.mpei.ac.ru

2. Абросимов Л.И. Анализ и проектирование вычислительных сетей: Учеб. пособие ¾ М.: Издательство МЭИ, 2000. ¾ 52 с.

3. Клейнрок Л. Вычислительные системы с очередями. М.: Изд-во “Мир”, 1979. ¾ 600с.

4. Tobagi F.A., Hunt V.B. “Performance Analysis of Carrier Sense Multiple Access with Collision Detection”. Computer Networks, vol.4, no.6, 1980.

5. Компьютерные сети: Учебный курс. /Пер. с англ. – М.: Издательский отдел “Русская редакция” ТОО “Channel Trading Ltd.”. – 2-е изд., испр. и доп. – 1998. – 696 с.

6. Шварц М. Сети связи: протоколы моделирования и анализ./ В 2-х ч. Ч.II. ¾ М.: Наука, Глав. ред. физ.-мат. лит-ры, 1992. ¾ 272с.