ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНО-КОМПРОМИССНОГО РЕШЕНИЯ МНОГОКРИТЕРИАЛЬНОЙ ЗАДАЧИ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ

Р. М. Акчурин, Е. И. Розенфельд

(Москва, Московский энергетический институт, Россия)

В настоящее время задачи планирования в экономических системах носят многокритериальный характер. Предлагаемые для решения указанных задач модели представляют собой оптимизационные модели, учитывающие интервальную неопределенность параметров [1].

	(1)
	(2)
	(3)
	(4)
	(5)

В статье [1] предложен алгоритм нахождения области Парето, состоящий из трех этапов. Поиск оптимально-компромиссного решения, которое является одной из точек области Парето, является весьма актуальной задачей. Настоящая статья как раз освещает вопросы поиска такого решения.

Одним из традиционных подходов при поиске глобального экстремума является переход к дискретному аналогу многокритериальной задачи с помощью введения множества пробных точек.

В качестве пробных точек в пространстве параметров мы использовали точки равномерно распределенных последовательностей, а именно точки так называемых -последовательностей [2], которые обладают наилучшими характеристиками равномерности среди всех известных в настоящее время равномерно распределенных последовательностей. Метод решения состоит из следующих этапов:

1. С помощью построения -последовательностей вся многомерная область допустимых значений задачи (1) – (5) систематически просматривается в пробных точках

2. В каждой пробной точке вычисляются значения всех критериев

3. Формулируется задача нечеткого математического программирования (НМП), в которой функции принадлежностей строятся с помощью предлагаемой процедуры (или каким-либо иным способом, более приемлемым, по мнению ЛПР)

4. Решением задачи НМП (см. пункт 3) будем считать некоторое нечеткое подмножество множества заданных альтернатив, функция принадлежности для элементов которого вычисляется по формуле

5. После осуществления свертки критерием в каждой -ой пробной точке стал соответствовать единственный числовой параметр . Для определения оптимальной точки из числа всех пробных точек необходимо было выбрать пробную точку с номером .

Рассмотрим процедуру построения функции принадлежности . Пусть в некоторой пробной точке вычислены значения всех критериев . Упорядочив вычисленные значения по возрастанию, получим следующий ряд:

,

(6)

где соответствующая перестановка индексов. Исключив повторяющиеся значения из ряда (6) получим новый ряд, в котором все элементы будут различны.

,

(7)

где соответствующее подмножество множества индексов .

Очевидно, что для каждого значения существует и единственное равное ему значение из ряда. Обозначим его порядковый номер через . Тогда функцию принадлежности можно вычислить как следующие отношение:

(8)

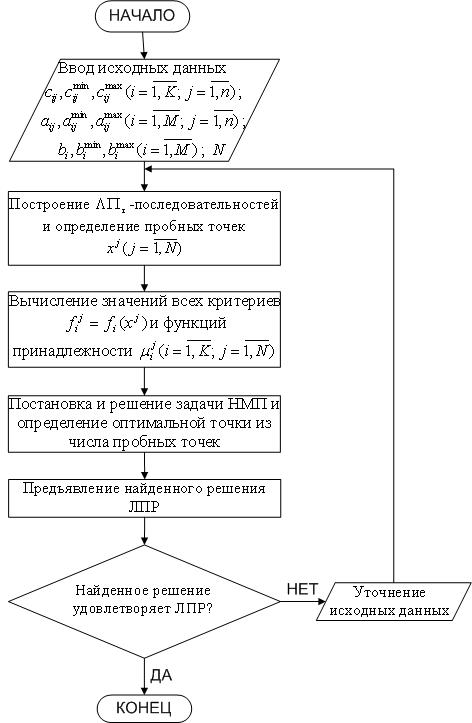
Нами было создано программное обеспечение, которое реализует приведенный выше алгоритм. Укрупненная блок-схема работы программы приведена на рисунке 1.

Рисунок 1

В заключении можно отметить, что если в результате опроса ЛПР исходную задачу (1) – (5) удается преобразовать к виду

	(9)
,	(10)

где – функции принадлежности нечеткой цели; – функции принадлежности нечеткого множества ограничений, то возможно применение методов, описанных в работе [3].

ЛИТЕРАТУРА

1. Акчурин Р. М., Розенфельд Е. И. Определение решений многокритериальной задачи оптимизации в условиях неопределенности. – Труды международной конференции «Информационные средства и технологии», т. 1, М., 2004, с. 152 – 155.

2. Соболь И. М., Статников Р. Б. Выбор оптимальных параметров в задачах со многими критериями. – М.: Наука, 1981 – 140с.

3. Оразбаев Б. Б. Методы многокритериального выбора и интеллектуальные системы принятия решений для управления производственными объектами при нечеткой исходной информации. – Автореф. дис. д-ра техн. наук. – М., 1996.