BC/NW 2006, №2, (9) :12.1

ОНТОЛОГИЧЕСКАЯ КЛАССИФИКАЦИЯ ДОКУМЕНТОВ

Белова М.С., Крюков А.Ф., Мещанинов Д.Г.

(Москва, Московский энергетический институт (технический университет), Россия)

Традиционный подход к документообороту рассматривает делопроизводственную сторону без рассмотрения специфических свойств и поведения документов, присущих их виду и контексту использования. Весьма актуальна задача разработки моделей, методов и программного обеспечения, позволяющих учесть существенные свойства и поведение документов (их онтологию), проявляемые ими во взаимосвязи с множеством различных объектов учёта, процессов обработки и участников. Рассматриваемая задача обусловлена множественной онтологической классификацией документов и новыми методами её решения такими как применение концептуального метамоделирования в рамках объектной парадигмы.

Рассмотрим произвольное конечное множество документов , где . Будем называть множество - множеством объектов, а номер элемента – идентификатором объекта [1].

Элементы множества описываются дискретными признаками . Каждый признак характеризуется множеством числовых или качественных значений , - номер значения признака , а - мощность множества значений признака (), - номер признака.

Значения признаков можно представить -мерным пространством:

…

Каждый объект из множества можно представить как точку в -мерном пространстве , и поставить каждому объекту в соответствие значение функции от -аргументов . Заметим, что значение функции может быть одинаковым для нескольких объектов, в том случае, если набор значений признаков будет совпадать, т.е. одна и та же точка в -мерном пространстве будет соответствовать нескольким разным элементам множества .

Необходимо выделить все возможные множества, каждое из которых характеризуется наличием у входящих в него объектов определенных признаков и их значений, т.е. в соответствии со значением функции или по каким-то другим отличительным характеристикам, которые невозможно описать числовыми или качественными значениями, например, по внешнему виду.

Разбить множество объектов на подмножества можно в соответствии с основаниями деления (в рамках терминов используемых в данной работе основание деление можно назвать аспектом) . В соответствии с каждым аспектом (где ) можно выделить множество классов , на которые можно разделить множество объектов. После выделения множества классов в соответствии с каждым аспектом, получается -мерное пространство:

…

,

где - множество классов (где - индекс, идентифицирующий класс на множестве , - мощность множества ), которые получились в результате деления множества объектов в соответствии с аспектом . Вектор назовем классификационной группировкой.

В соответствии со значением функции от аргументов , которым характеризует объект, а также в соответствии с характеристиками, которые невозможно описать числовыми или качественными значениями, элемент можно представить как точку в -мерном пространстве . Объекту в соответствие можно поставить значение функции от -аргументов , где , …, - индекс, идентифицирующий класс внутри одной классификационной группы.

Рассмотрим множество классов - классификационную группировку. Такое множество является частично упорядоченным множеством, то есть на данном множестве задано отношение частичного порядка между элементами [1]. Отношение частичного порядка обладает свойствами рефлексивности, транзитивности и антисимметричности.

Рефлексивность означает, что любой элемент множества находится в отношении с самим собой. Формальная запись свойства рефлексивности отношения £ выглядит следующим образом:
, где .

Свойство транзитивности указывает на то, что если существует цепочка из (трех) элементов, связанных отношением £, то первый и последний элементы этой цепочки можно связать тем же отношением. Это свойство гарантирует построение графа отношения частичного порядка на множестве в виде «решетки». Формальная запись свойства транзитивности для отношения £ выглядит следующим образом:
.

Антисимметричность – свойство, которое разрешает наследование только в одном направлении и запрещает его в противоположном направлении. Формальная запись свойства антисимметричности для отношения £ выглядит следующим образом:
.

Для формализации модели наследования использована диаграмма Хассе. На диаграмме Хассе точками или кружками представляются элементы множества, причем если , то элемент располагается ниже элемента , при этом элементы соединяются линией, если не существует другого элемента , такого, что и . Приведем пример диаграммы Хассе для представления отношения включения (характерное отношения частичного порядка) на множестве всех подмножеств .

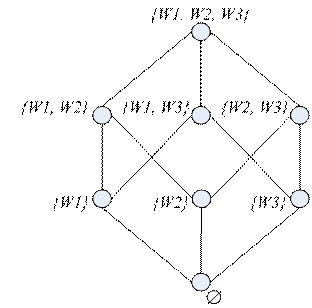
Рассмотрим модель наследования на простом примере классификации множества документов. Множество документов можно разбить на подмножества в соответствии с аспектом «Назначение документа». В соответствии с выбранным аспектом образуется классификационная группировка ={Организационный, Распорядительный, Нормативный}. Расширим множества классов данной группировки. Организационные документы делятся на уставы, положения, руководства, инструкции. В свою очередь инструкции делятся на должностные инструкции, инструкции по эксплуатации систем оборудования, производственные инструкции. Ниже представлена диаграмма Хассе для классификационной группировки .

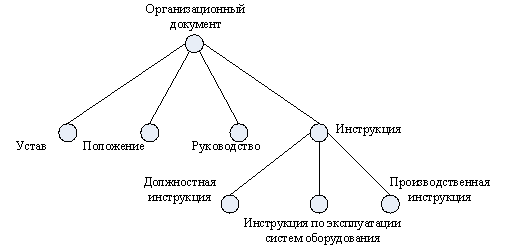
В результате получена математическая модель схемы классификации объектов, основными элементами которой являются множество объектов ; множество признаков, которыми характеризуется объект - ; множество аспектов в соответствии с которыми образуются частично упорядоченные множества классов - классификационные группировки. На множестве с помощью отношения частичного порядка описывается наследственная связь между элементами множества.

Полученная модель применена для реализации комплекса классификации документов для системы электронного документооборота в соответствии с алгоритмом последовательности действий построения схемы классификации.

ЛИТЕРАТУРА

1. Фролов А.Б., Андреев А.Е., Болотов А.А., Коляда К.В. Прикладные задачи дискретной математики и сложность алгоритмов. М.: МЭИ, 1997. – 312 с.