BC/NW 2006, №2, (9) :12.4
РАЗРАБОТКА ОРТОГОНАЛЬНЫХ МНОГОМЕРНЫХ БАНКОВ
ФИЛЬТРОВ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ
КЭЛИ
М.К. Чобану
Москва, Московский энергетический институт (технический университет)
Цифровые многоскоростные банки фильтров (БФ) были впервые введены в [1], где они использовались для сжатия речи. В
дальнейшем они стали шире применяться, главным образом, для кодирования
подполос речи, статических изображений и видео [2].
Речь шла о синтезе систем, достигающих точного восстановления сигнала (ТВС) в одном
или нескольких измерениях, от двухканальных ортогональных банков до
многоканальных систем. Для выполнения этих требований все усилия были
сконцентрированы на фильтрах, имеющих дробно-рациональные функции
преобразования, т.е. на линейных инвариантных к сдвигу системах.
Основной подход к синтезу неразделимых ММ цифровых фильтров в данной
работе является аналитическим. Далее описывается метод аналитического или прямого синтеза
неразделимых ММ цифровых фильтров с КИХ для ММ многоскоростных систем [3]. Предложена методика синтеза ММ цифровых
фильтров, удовлетворяющих заданному набору требований. В отдельных случаях, при
наличии свободных параметров при синтезе фильтров, проведена оптимизация
частотных или иных характеристик, позволяющая вычислить свободные параметры.
Основные требования, которым должен удовлетворять ММ фильтр, являющийся
частью ММ многоскоростной системы, обычно включают:
1. Свойство точного восстановления сигнала.
2. Свойство линейности ММ фазы.
3. Фильтр имеет действительную ММ конечную импульсную характеристику
(фильтры с БИХ выходят за рамки данной работы).
4. Заданная ММ полоса пропускания/задерживания фильтра.
5. Заданная гладкость фильтра.
6. Свойство ортогональности или биортогональности.
Синтезируемые фильтры могут быть
неразделимыми и метод аналитического синтеза должен позволять строить
такие фильтры.
Свойство ортогональности используется достаточно часто в системах
преобразования ММ сигналов. Это объясняется тем, что при этом сохраняется
энергия сигнала и тем самым не происходит увеличения энергии ошибок в сигнале
(из-за квантования или по другим причинам). А также тем, что при выполнении
определенных условий становится возможным строить базисы вейвлет функций.
Lостаточно успешным является подход, основанный на построении ММ полифазных
полиномиальных матриц. В [2] сформулирована задача синтеза параунитарных
матриц с действительными коэффициентами U(z) таких, что
(1)
Известно [4], что параунитарные матрицы могут быть
представлены с помощью обратного преобразования Кэли в следующем виде: где полиномиальная матрица H(z) связана с U(z) с помощью прямого преобразования
Кэли:
(2)
Матрица H(z) является эрмитовой
косо-симметрической матрицей с действительными коэффициентами:
(3)
Применение преобразования Кэли позволяет перейти от решения нелинейных
уравнения (для неизвестных коэффициентов параунитарной матрицы U(z)), обеспечивающих выполнение (1), к линейным уравнениям для построения
матрицы H(z) в соответствии с (3). В последнее время стали появляться работы,
связанные с таким подходом к решению данной задачи [5].
В случае синтеза ортогональных БФ с бесконечной импульсной
характеристикой, преобразование Кэли позволяет наиболее простым способом
получить полную параметризацию всех возможных ортогональных ММ
многоскоростных систем. Для этого достаточно выбрать соответствующим образом
эрмитову косо-симметрическую матрицу H(z).
В случае синтеза ортогональных БФ с конечной импульсной характеристикой,
что является предметом настоящего исследования, ситуация значительно более
сложная. Дело в том, что при выполнении прямого преобразование Кэли (2) в общем случае H(z) может стать БИХ полиномиальной
матрицей. Поэтому необходимо выполнение особых условий, обеспечивающих
получение в конечном итоге ортогональной КИХ полиномиальной матрицы U(z). Подставляя в (2), получим, что где adj обозначает матрицу алгебраических
дополнений для элементов матрицы I+U(z). Если обозначить матрицу в числителе
через , а определитель в знаменателе через Q(z), тогда
Необходимыми и достаточными условиями построения параунитарной КИХ
матрицы U(z) являются следующие равенства:
•
• то есть где
•
• .
Из параунитарной матрицы U(z) далее строятся низкочастотный и
высокочастотный фильтры банка синтеза [2]:
Для построения вейвлет базисов и основанного на них кратномасштабного
анализа [3,6], необходимо, чтобы построенный низкочастотный
фильтр был регулярным. С этой целью необходимо приравнять нулю первые N смешанных производных:
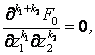, где при .
Ниже приведен расчет двухканальной двумерной ортогональной
многоскоростной системы. Для N=2 решение уравнений, обеспечивающих
наличие КИХ у БФ, дало наряду с разделимым вариантом, соответствующим
ортогональной функции daubechies-4 или db4, также и неразделимый ортогональный
фильтр. Он описывается так:
– вспомогательные многочлены:
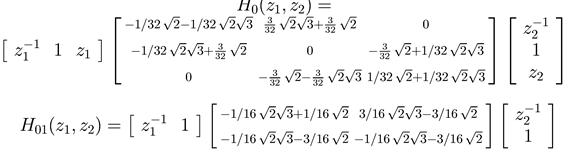
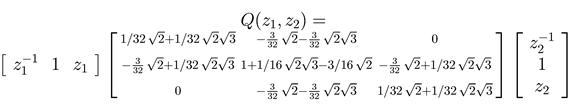
– низкочастотный и высокочастотный фильтры:
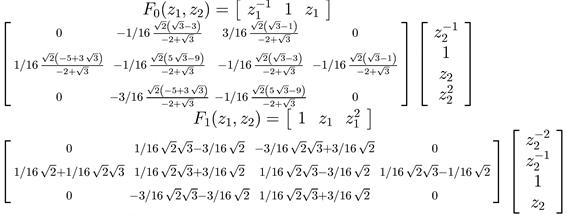
Применение преобразования Кэли дает полную параметризацию всех
ортогональных ММ БФ, включая БФ с БИХ и с КИХ. Предложенный метод синтеза
ортогональных банков фильтров с КИХ работает при произвольном числе каналов,
для любой размерности и для заданной степени гладкости фильтров.
Синтезированные БФ могут использоваться в системах преобразования ММ сигналов с
целью их сжатия, передачи по каналам связи, удаления шумов и др.
Литература
1.
Croisier A., Esteban D., Galaud C. Perfect channel splitting by use of
interpolation/decimation/tree decomposition techniques// Intern. Confer.
Inform. Sci. Syst. —
2.
Vaidyanathan P. P. Multirate Systems and Filter Banks. —
3.
Tchobanou M. Design of
multi-dimensional wavelets and multi-dimensional multirate
systems (in English) // Труды Межд. конф. "Wavelets and
Splines" июль 3-8, 2003. — Санкт Петербург: 2005. — Pp.118–133.
4. Гантмахер Ф. Теория
матриц. — Москва: Наука, 1988. — 550 с.
5. Zhou J., Do M., Kovaĉević J. Special paraunitary matrices,
Cauley transform, and multidimensional orthogonal filter
banks // IEEE Trans. Image Proc. — 2006. — Feb. — Vol. 15, no. 2. — Pp. 511–519.
6. Чобану М. К., Максименко И.Е. Синтез двухканальных
многомерных вейвлетов и их применение для сжатия изображений // Вестник МЭИ.
— 2006.