BC/NW 2006, №2, (9) :12.7
АСНИ «МАСТЕРСКАЯ ГРАФ-МОДЕЛЕЙ»:
ПОДСИСТЕМА СТРУКТУРНОГО СПЕКТРАЛЬНОГО АНАЛИЗА ДЕРЕВЬЕВ
В.А. Кохов, С.А. Горшков, Али Рашид Ибрахим, Малатх
Рахим Джасим
(Москва, Московский энергетический институт (ТУ),
Россия)
Рассмотрены
классы задач структурного спектрального анализа графовых моделей объектов,
решаемых в подсистеме «СС-анализ деревьев». Приведены
примеры графовых моделей, позволяющих впервые анализировать сложность, сходство
и симметрию деревьев с учетом расположения фрагментов.
В рамках внедрения новых информационных
технологий в учебный процесс разработана подсистема АСНИ «GMW»,
включающая 9 программных комплексов (ПК), позволяющих решать задачи, входящие в
инвариантное ядро задач структурного спектрального анализа и синтеза деревьев
[1]:
1. Построение g-моделей и b-моделей, характеризующих деревья в расширяемых
базисах структурных дескрипторов (СД) с учетом расположения фрагментов
заданного вида [2,3].
2. Анализ симметрии деревьев: (2.1) Построение
порождающего множества и всей группы автоморфизмов дерева (Aut(G)).
Вычисление основных характеристик Aut(G); (2.2)
Построение порождающего множества и всей t-группы автоморфизмов дерева (Autt(G)). Вычисление характеристик Aut
t(G);
3. Различение деревьев: (3.1) Изоморфизм деревьев; (3.2)
Изоморфное вложение дерева в дерево; (3.3) Определение всех изоморфных и
канонических изоморфных вложений дерева в дерево.
4. Различение расположения фрагментов в топологии
деревьев: (4.1) Различение расположения фрагментов типа t с
точностью до орбит Aut t(G); (4.2)
Различение расположения фрагментов типа t с точностью до классов t-эквивалентности. Отношение t-эквивалентности задается базисом СД; (4.3) Различение
расположения фрагментов с точностью до вложения орбит фрагмента типа t1 в орбиты
фрагмента типа t2; (4.4) Различение расположения фрагментов с точностью
до вложения классов t-эквивалентности расположения фрагмента типа t1 в классы t-эквивалентности расположения фрагмента типа t2, где t1Í t2.
5. Анализ
сложности деревьев; (5.1) Вычисление индексов; (5.2) Вычисление
вектор-индексов; (5.3) Вычисление
расширенной матрицы b-модели;
6. Анализ сходства деревьев: (6.1) По подструктурному
подходу на основе максимального общего фрагмента (МОФ); (6.2) По обобщенному
подструктурному подходу на основе g-моделей или b-моделей или b(g)-моделей.
7.
Анализ сходства
расположения фрагментов в топологии дерева: (7.1) С точностью до орбит
фрагментов заданного типа; (7.2) С точностью до классов t-эквивалентного расположения фрагментов заданного
типа.
8.
Прорисовка
диаграмм деревьев и их g-моделей с учетом симметрии.
9.
Конструктивное
перечисление деревьев и генерация семейств деревьев с заданными ограничениями.
Архитектура АСНИ «GMW», в рамках которой функционируют программ-ные
комплексы подсистемы «СС-анализ деревьев» приведена на рис. 1.
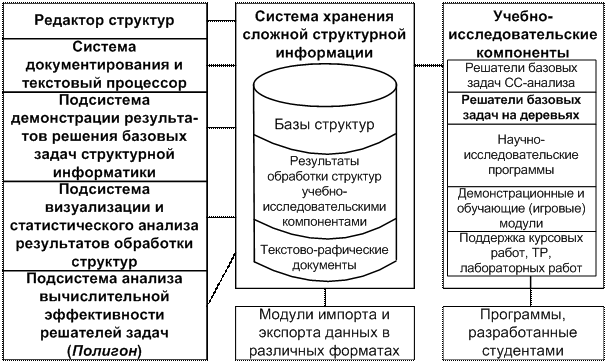
Рис. 1.
Функциональное наполнение АСНИ «Мастерская граф-моделей»
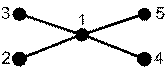
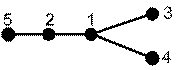
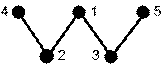
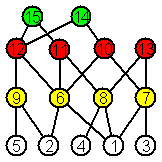
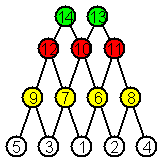
Рассмотрим пример анализа
сходства деревьев (рис. 2) с использованием g-модели SHPlScwÍPlScw(G),
называемой цветным графом цепей (ЦГЦ) [2,3].
Определяя МОФ для каждой
пары ЦГЦ, получаем два варианта вычисления расстояний и два варианта вычисления
коэффициентов сходства:
• d1(G1,G2) =úV(HPlScwÍPlScw(G1))ê+úV(HPlScwÍPlScw(G1))ê - 2úV(MCS)ê;
•
d2(G1,G2)
=úV(HPlcwÍPlcw(G1))ê+úE(HPlcwÍPlcw(G1))ê+úV(HPlcwÍPlcw(G2))ê+
+úE(HPlcwÍPlcw(G2))ê-
2(úV(MCF)ê+úE(MCF)ê);
•
MSI1(G1,G2) =ú MCS(HPlScwÍPlScw(G1),HPlScwÍPlScw(G2))ê2
/úF1(G1)×F1(G2)ê;
•
MSI2(G1,G2) =ú MCF(HPlcwÍPlcw(G1),HPlcwÍPlcw(G2))ê2
/úF2(G1)×F2(G2)ê,
где
F1 (F2) - число вершин (сумма числа вершин и рёбер) в ЦГЦ дерева.
|
G1 |
G2 |
G3 |
|
Цветной граф
цепей gp(G1) |
Цветной граф цепей gp(G2) |
Цветной граф цепей gp(G3) |
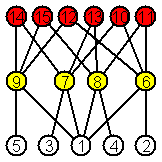
Рис. 2. Диаграммы графов и их цветных
графов цепей (на первом уровне расположены вершины исходного дерева, на втором
– вершины-цепи длины 1, на третьем – вершины-цепи длины 2, на четвертом –
вершины-цепи длины 3)
Для деревьев G1-G3
получим
результаты, приведенные в табл. 1 (значения d1,d2 под главной диагональю, а значения MSI1, MSI2 -
над диагональю).
Таблица 1
|
Расстояния
d1,d2 и коэффициенты сходства MSI1 |
Расстояния
d1,d2 и коэффициенты сходства MSI2 |
||||||||||||||
|
|
G1 |
G2 |
G3 |
|
gp1 |
gp2 |
gp3 |
|
G1 |
G2 |
G3 |
|
gp1 |
gp2 |
gp3 |
|
G1 |
0 |
0,64 |
0,36 |
gp1 |
0 |
0,53 |
0,48 |
G1 |
0 |
0,79 |
0,61 |
gp1 |
0 |
0,76 |
0,51 |
|
G2 |
2 |
0 |
0,64 |
gp2 |
8 |
0 |
0,69 |
G2 |
2 |
0 |
0,79 |
gp2 |
9 |
0 |
0,65 |
|
G3 |
4 |
2 |
0 |
gp3 |
9 |
5 |
0 |
G3 |
4 |
2 |
0 |
gp3 |
19 |
13 |
0 |
Переходя
последовательно от ЦГЦ длины 0 к длине q, а затем к g-моделям,
учитывающим расположение поддеревьев и лесов, получим универсальный метод для
иерархического анализа сходства деревьев, с последовательным уточнением
результатов. В табл. 2 приведены примеры матричного представления расширенной b-модели PlScwÍPScw для G2
и b-модели VlÍPScw для HPlcwÍPlcw(G2) [2]. В табл. 3 приведены результаты анализа сходства с
использованием b-моделей PlcwÍPcw при монотонном наращивании
базиса СД.
Применение b-моделей позволяет провести иерархический анализ
сходства графов с
последовательным уточнением результатов по направлениям:
1. Индекс (ISC), вектор-индекс (V_ISC),
матрица b-модели (M_Irc);
2. Вектор-индекс вкладов Irc(f
t), Irc(f t(c)), Irc(fi t), матрица M_Irc.
Вычисление МОФ для пар b-моделей в стратифицированной системе приводит к возможности исследования тенденций изменения сходства де- ревьев
ещё по трём направлениям стратификации
самой b-модели: (1) монотонное расширение базисов СД; (2)
монотонное расширение типов фрагментов; (3) монотонное расширение как базисов
СД, так и типов фрагментов.
Таблица 2
|
PlScwÍPlSc |
P0 |
P1 |
P2 |
P3 |
|
Irc(fi t) |
Irc(f
t(c)) |
Irc(f
t) |
|
VlÍPlSc |
P0 |
P1 |
P2 |
P3 |
P4 |
|
Irc(fi t) |
Irc(f
t(c)) |
|
2 |
1 |
2 |
2 |
0 |
0,057 |
0,057 |
0,392 |
2 |
1 |
2 |
6 |
10 |
10 |
0,0648 |
0,0648 |
|||
|
1 |
1 |
3 |
1 |
0 |
0,050 |
0,050 |
1 |
1 |
3 |
10 |
8 |
4 |
0,0350 |
0,0350 |
||||
|
5 |
1 |
1 |
1 |
2 |
0,110 |
0,110 |
5 |
1 |
1 |
2 |
4 |
8 |
0,0451 |
0,0451 |
||||
|
3,4 |
1 |
1 |
2 |
1 |
0,087 |
0,174 |
3,4 |
1 |
1 |
3 |
5 |
11 |
0,0613 |
0,1225 |
||||
|
12 |
0 |
1 |
3 |
0 |
0,056 |
0,056 |
0,314 |
6 |
1 |
5 |
10 |
10 |
2 |
0,0285 |
0,0285 |
|||
|
25 |
0 |
1 |
1 |
2 |
0,101 |
0,101 |
9 |
1 |
3 |
4 |
8 |
12 |
0,0710 |
0,0710 |
||||
|
13,14 |
0 |
1 |
2 |
1 |
0,079 |
0,157 |
7,8 |
1 |
4 |
5 |
11 |
15 |
0,0901 |
0,1802 |
||||
|
314 |
0 |
0 |
1 |
0 |
|
0,016 |
0,016 |
0,217 |
|
13 |
1 |
2 |
6 |
6 |
14 |
|
0,0784 |
0,0784 |
|
213,214 |
0 |
0 |
1 |
1 |
0,054 |
0,108 |
10,11 |
1 |
3 |
8 |
10 |
13 |
0,0802 |
0,1604 |
||||
|
125 |
0 |
0 |
1 |
2 |
0,093 |
0,093 |
12 |
1 |
4 |
8 |
6 |
14 |
0,0795 |
0,0795 |
||||
|
3125,4125 |
0 |
0 |
0 |
1 |
0,039 |
0,077 |
0,077 |
14,15 |
1 |
2 |
5 |
12 |
10 |
0,0672 |
0,1345 |
|||
|
Slw |
5 |
12 |
20 |
14 |
51 |
1 |
1 |
Slw |
15 |
40 |
88 |
128 |
162 |
433 |
1 |
|||
|
Sw |
1 |
3 |
5 |
7 |
16 |
a(P0/P)=1 |
Sw |
1 |
2 |
2 |
2 |
2 |
9 |
a(P0/P)=1 |
||||
|
WF |
5 |
4 |
4 |
2 |
15 |
a(P1/P)=1 |
WF |
15 |
20 |
44 |
64 |
81 |
224 |
a(P1/P)=1 |
||||
|
ISC(Pj) |
1 |
3 |
9 |
31 |
44 |
a(P2/P)=1 |
ISC(Pj) |
1 |
3 |
9 |
31 |
106 |
150 |
a(P2/P)=1 |
||||
|
V_ISC |
5 |
12 |
36 |
62 |
115 |
a(P3/P)=1 |
V_ISC |
15 |
60 |
396 |
1984 |
8586 |
11041 |
a(P3/P)=1 |
||||
Таблица 3
|
|
ISC |
V_ISC |
M_Irc |
|||||||||
|
Пары |
P0-1 |
P0-2 |
P0-3 |
P0-4 |
P0-1 |
P0-2 |
P0-3 |
P0-4 |
P0-1 |
P0-2 |
P0-3 |
P0-4 |
|
G1,G2 |
0 |
18 |
44 |
44 |
0 |
18 |
80 |
80 |
210 |
2478 |
8058 |
8058 |
|
G1,G3 |
0 |
27 |
35 |
141 |
0 |
27 |
89 |
195 |
1260 |
10899 |
27639 |
49899 |
|
G2,G3 |
0 |
9 |
9 |
97 |
0 |
9 |
9 |
115 |
630 |
3465 |
9045 |
38725 |
Подсистема включает 7 DLL, общим
объемом 4,6 Мб, созданных в средах Microsoft Visual С++ .NET, С++ Builder 6 и Delphi 7 и позволяет анализировать базы деревьев с числом
вершин до 5000 на современных ПЭВМ.
ЛИТЕРАТУРА
1. Кохов В.А. Концептуальные и математические модели сложности
графов. М. Издательство МЭИ, 2002. – 160 с.
2. Кохов В.А. Граф-модели в структурном спектральном анализе
систем. Тезисы докладов международной конференции «Информационные средства и
технологии», МФИ-2004, Т.1, М, МЭИ, 2004. – С.211-214.
3. Кохов В.А. Модели и методы для анализа сходства структур систем с
учетом сходства расположения фрагментов. Тезисы докладов научной сессии
МИФИ-2006. Т3. Интеллектуальные системы и технологии. М. МИФИ. 2006. –
С.144-145.