BC/NW 2006, №2, (9) :13.2

 

СТЕГАНОГРАФИЧЕСКИЙ АНАЛИЗ ТЕКСТОВЫХ ФАЙЛОВ-КОНТЕЙНЕРОВ ПРИ РАБОТЕ В ВЫЧИСЛИТЕЛЬНЫХ СЕТЯХ

 

Колошеин Ю. А.

 

(Москва, Московский Энергетический Институт (Технический Университет), Россия)

 

На протяжении всей своей истории человечество защищало свои секреты, однако применяемые комплексы административно-технических мер, направленных на обеспечение требуемого уровня, не всегда могли противостоять новым видам атак, например, стеганографическим атакам, использующим в качестве контейнера текстовый файл. Стеганография – новейшая область [1] computer science, занимающаяся вопросами защиты информации. Настоящий доклад посвящен вопросам стеганографического анализа текстовых файлов-контейнеров, а именно – обнаружения факта наличия в контейнере встроенной информации.

 

Анализируя текстовые файлы-контейнеры, заполненные с помощью программных продуктов, приведенных в [2, 3], заметим наличие во многих контейнерах так называемых маркеров наличия в контейнере секретного сообщения; обычно такой маркер занимает 1 байт (в качестве примера можно привести FFENCODE, Secure Engine 4.0). Заметим, что часть этих маркеров может «выбиваться» из общего текста-контейнера, например, не алфавитно-цифровые символы кодировки ANSI/ASCII.

В этом случае анализ сильно упрощается, так как наличие такого маркера позволяет однозначно установить факт передачи информации (вернее то, что в анализируемый контейнер встроена информация – в данном контексте это одно и тоже).

Гораздо сложнее дело обстоит в случае, если стеганографический алгоритм, с помощью которого в текстовый контейнер была встроена информация, относится к классу вычислительно стойких стегоалгоритмов [4]. Как обнаружить факт наличия встроенной информации именно в таком контейнере?

В рамках проведенных исследований было выделено два класса текстов-контейнеров: техническая литература, художественная литература.

В основу исследований была положена идея построения образа идеального пустого контейнера, сравнивая с которым любой отдельно взятый контейнер можно судить о наличии либо отсутствии информации в последнем с определенной вероятностью. Необходимо выбрать параметры, наиболее информативные для данного конкретного случая.

В ходе анализа пустого и заполненного контейнеров были выявлены следующие особенности (вытекают из алгоритма встраивания [4]):

1.     размеры пустого и заполненного контейнеров совпадают;

2.     длина строки (текст моноширинный!) пустого и заполненного контейнеров совпадают;

3.     количество пробелов (именно с их помощью в текст-контейнер встраивается информация) пустого и заполненного контейнеров совпадают.

В результате сравнительного анализа статистических характеристик пустого и заполненного контейнеров был выявлен наиболее удобный с точки зрения стеганографического анализа текста-контейнера параметр – средняя длина интервала.

Пусть  – количество средних длин интервалов для контейнера Т.

 = max(Ij), где Ij – количество интервалов в j-ой строке контейнера Т, jÎ[1, n], n – число строк в Т.

Пусть - длина i-й средней длины интервала.

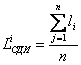, где li – длина i-го интервала, iÎ[1, NСДИ]

Примечание. Исследования показали, что средняя длина интервала при встраивании информации в контейнер меняется более сильно, чем другие параметры, следовательно, средняя длина интервала более информативна.

На основе средних длин интервалов был построен образ пустого контейнера. В связи с тем, что для построения идеального или близкого к идеальному образа пустого контейнера необходим анализ очень большого количества достаточно больших по объему текстов, были введены верхняя и нижняя граница образа пустого контейнера, в качестве которых были взяты минимальные и максимальные значения параметров.

Заметим, что для каждого класса текстов-контейнеров образ пустого контейнера будет свой, то есть в общем случае образы пустых контейнеров для разных классов тестов могут сильно отличаться. Это утверждение подтверждается экспериментом.

В таблице 1 приведены образы, в которые с помощью авторского программного обеспечения была встроена информация. Совокупность средних длин интервалов и образ контейнера в данном контексте одно и тоже.

 

Таблица 1. Образ заполненного контейнера (научно-технический текст)

 

№

Контей-нер

Всего
интервалов

Удельная длина интервала

1

2

3

4

5

6

7

8

9

1

File1.txt

518

2,25

2,27

2

1,75

1,75

1,5

1,5

1,2

1

2

File2.txt

782

2,25

2,27

2,1

1,72

1,76

1,5

1,5

1,2

1,1

3

File3.txt

644

2,23

2,29

2,2

1,73

1,78

1,3

1,7

1,1

1,1

4

File4.txt

1123

2,27

2,25

1,9

1,76

1,74

1,6

1,4

1,1

0,9

5

File5.txt

347

2,24

2,28

2,1

1,74

1,74

1,6

1,4

1,2

1,0

6

File6.txt

654

2,27

2,25

2

1,75

1,77

1,5

1,5

1,1

0,8

7

File7.txt

519

2,28

2,24

2

1,76

1,74

1,4

1,3

1,1

0,9

 

Обнаружение встроенной в контейнер информации основано на сравнении образа пустого и заполненного контейнеров. Если образы сильно отличаются, то с определенной вероятностью считаем, что данный контейнер содержит в себе встроенную информацию. Если образы отличаются незначительно, считаем контейнер (также с определенной вероятностью). Для наглядности построим гистограмму образа пустого контейнера, и на этой же гистограмме отобразим образ заполненного контейнера (file1.txt). Гистограммы приведены на рис. 1 (красным цветом изображен образ пустого «идеального» контейнера, а зеленым – образ анализируемого заполненного контейнера).

Заметим, что если контейнер заполнен не полностью, обнаружить встроенную в контейнер информацию сложнее, так как образы в общем случае будут отличаться слабее, чем в случае полного заполнения контейнера.

 

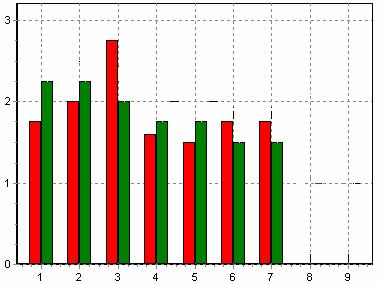
Рисунок 1 – гистограммы образов пустого идеального и заполненного контейнеров

 

В результате проведенной работы были выявлены характеристики контейнера, анализируя которые, можно качественно ответить на вопрос: содержит анализируемый контейнер встроенную информацию или нет? В ходе дальнейшей работы, возможно, удастся получить количественные оценки вероятностей обнаружения информации в контейнере (вероятность обнаружения информации при условии, что она там действительно есть, при условии, что ее там нет; вероятность необнаружения информации при условии, что ее там нет, а также при условии, что она там есть). Возможно, удастся выявить порог обнаружения, т.е. количество информации, которое нельзя обнаружить для стеганографического метода [4].

ЛИТЕРАТУРА

1.     Грибунин В.Г., Оков И.Н., Туринцев И.В. Цифровая стеганография. – М.: СОЛОН-Пресс, 2002. – 272 с.

2.     Мельников Ю.Н., Колошеин Ю.А. Возможности сокрытия банковской информации в текстовых файлах. // Банковские технологии. – 2003. – №11. – С. 35-37.

3.     Мельников Ю.Н., Колошеин Ю.А. Возможности сокрытия банковской информации в текстовых файлах. // Банковские технологии. – 2003. – №12. – С. 40-44.

4.     Колошеин Ю.А. Разработка алгоритма стеганографического сокрытия защищаемой информации в текстовом файле. Труды IX Международной научно-практической конференции "Стратегия развития пищевой промышленности". Выпуск 8 (т. II), Москва,
13-14 мая 2003 г.