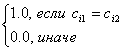BC/NW 2006, №2, (9) :4.5
НЕЧЁТКОЕ ОТНОШЕНИЕ НЕРАЗЛИЧИМОСТИ ДЛЯ
ОБРАБОТКИ ТАБЛИЦ РЕШЕНИЙ НА ОСНОВЕ ТЕОРИИ ПРИБЛИЖЁННЫХ МНОЖЕСТВ[1]
О.В. Виноградов
(Москва, Московский энергетический институт
(Технический университет), Россия)
Язык таблиц решений (ТР) получил широкое
распространение при автоматизации процессов принятия решений, проектирования,
диагностики и контроля, в имитационном моделировании ([1]). Использование
табличных баз знаний (БЗ) в системах поддержки принятия решений (СППР) не
сводится только к принятию решения по заданному входному вектору. Ещё на этапе
разработки СППР могут ставиться различные задачи обработки ТР, в том числе
проверка определённых свойств таблиц решений и их оптимизация по некоторым
критериям. Такого рода обработка ТР требуется как при первичной разработке
СППР, так и при её последующей динамической модификации. В связи с этим
возникает необходимость построения комплекса алгоритмов, позволяющих
реализовывать обработку таблиц решений за минимальное время. Желательным также
является наличие единой теоретической базы у этих алгоритмов, что позволяет
использовать в них общие структуры данных, сокращая тем самым общее время
вычислений. На данный момент известны несколько алгоритмов проверки
полноты/непротиворечивости ТР, однако они разрозненны, часть из них имеет
достаточно высокую вычислительную сложность. Методы оптимизации ТР исследованы
в меньшей степени. Для решения задач обработки ТР предлагается использовать
аппарат приближённых множеств ([3]). Для этого требуется построить расширение
базовой теории приближённых множеств с целью адаптации её понятий к семантике
таблиц решений.
Введём основные используемые понятия. ТР зададим набором 
([1]). Четверка 
есть традиционное
определение ТР, где 
– множество условий или идентификаторов
условий, рассматриваемых как координаты векторов описания ситуаций или
состояний (векторов данных), 
– множество действий или идентификаторов
действий, рассматриваемых как координаты векторов действий; 
и 
, где 
или 
, – матрицы соответствия между векторами данных (состояниями) и действиями. Компонент 
может содержать дополнительную информацию
(например, о коэффициентах применимости продукций, сложности вычисления
условий, отношениях между ними и т. п.). В матрице 
допускается
использование символов безразличия «*», указывающих на то, что определённое
условие несущественно для определения применимости данного правила. Если
правило содержит символы «*», то оно называется обобщённым, в противном случае
правило называется простым. При практическом применении ТР необходимо уметь
гарантировать наличие у ТР некоторых свойств, придающих процессу принятия
решений на их основе надёжность и эффективность. К таким свойствам относятся
полнота, непротиворечивость и неизбыточность. Последнее свойство может быть обобщено
до понятия оптимальности ТР по некоторому критерию, в качестве таких критериев
можно также рассматривать минимальное число правил в ТР, максимальное число
символов «*» в матрице 
и др.
Предметом рассмотрения в теории приближенных множеств
являются универсум 
(конечное множество однотипных объектов
предметной области) и заданное на нем бинарное отношение 
,
называемое отношением неразличимости
(indiscernibility relation).
На практике рассматривают универсум в виде таблицы с данными, где каждый объект
представляется строкой значений. Вводится формальное понятие решающей системы (decision system) вида 
, где – универсум, а 
и 
– множества атрибутов-условий и
атрибутов-решений, описывающих свойства объектов универсума. Для произвольного
подмножества атрибутов отношением ‑неразличимости
называется отношение 
.
Отношение неразличимости является центральным в теории приближенных множеств,
на основе него вводятся все остальные понятия теории, в том числе аппроксимации
множеств, матрицы и функции различимости, редукции и др. Отношение
неразличимости, введённое выше, принадлежит к классу отношений эквивалентности.
На практике встречаются случаи, когда удобнее рассматривать отношения
неразличимости более общего вида, для которых, например, не выполняются
свойства транзитивности и/или симметричности.
Была поставлена задача поиска методов обработки ТР на
основе теории приближённых множеств, в том числе для проверки свойств и
оптимизации таблиц решений. Формальный изоморфизм структуры ТР (при отсутствии
компонента ) и
решающих систем очевиден, но традиционная
интерпретация информационного содержимого этих структур различается. Если
представить экспертную ТР в формализме приближенных множеств, то к ней будут
применимы все методы обработки решающих систем. Таким образом, получаем
практически готовые методы обработки ТР, решающие задачи проверки некоторых
свойств ТР, выделения детерминированной подтаблицы из недетерминированной ТР и
оптимизации ТР по числу используемых условий и продукционных правил. Интересно,
что получаемый эффект достигается при кодировании информации более высокого
уровня (т.е. продукционных правил из ТР) в форме, характерной для
низкоуровневой информации («сырых» данных) с последующим извлечением
оптимизированных правил.
Массовость наличия символов безразличия в реальных ТР
является существенной особенностью решающих систем, получаемых при обработке
ТР. Полное раскрытие всех символов пропуска едва ли возможно, так как ведёт к
экспоненциальному росту размеров таблиц, усложняя их обработку. Поэтому
целесообразнее оставлять символы пропуска без изменений, усложняя топологию
отношения неразличимости. Пока в ТР отсутствуют символы «*» отношение
неразличимости на множестве правил строится простым сравнением значений условий
на правилах. Но присутствие символа безразличия существенно усложняет картину.
Казалось бы, можно интерпретировать символ безразличия как неизвестное значение
данного условия. В терминах предиката различимости discerns такое отношение может быть записано в виде 
. Это
отношение является рефлексивным и симметричным, но не обладает свойством
транзитивности.
На первый взгляд такое интуитивное построение
неразличимости на основе символа * является вполне естественным. Однако можно
построить пример, из которого видно, что трактовка символа * как простого
отсутствия данных (безразличия) приводит к нежелательным последствиям:
неразличимыми становятся правила, распознающие существенно различающиеся наборы
входных векторов. В ходе исследований стала очевидной необходимость перехода к
нечёткому отношению неразличимости, так как только оно может адекватно передать
степень неразличимости обобщённых правил. Функция принадлежности нечёткого
отношения неразличимости решающих правил ТР с расширенным входом при сравнении
по одному условию 
приведена в таблице 1, где через 
обозначено множество значений, которые может
принимать условие .
Отношение неразличимости по нескольким условиям строится пересечением отношений
по единичным условиям ([Леон’03]) с применением оператора произведения
вещественных чисел (*-пересечение): 
.
|
Табл. 1.
Функция принадлежности |
||||||||||||||
|
Разработанные на основе введённого отношения
неразличимости алгоритмы проверки непротиворечивости и оптимизации ТР были
реализованы в расширенной версии системы СИМПР-Windows 2.2, разрабатываемой на кафедре Прикладной математики
МЭИ (ТУ). Работы по данной тематике выполнялись в научной группе д.т.н.
проф. Вагина В.Н. и д.т.н. проф.
Еремеева А.П. в плане НИР кафедры Прикладной математики МЭИ (ТУ) по тематике
«Разработка систем поддержки принятия решений на основе аппарата нетрадиционных
логик».
ЛИТЕРАТУРА
1. Еремеев А. П. О корректности продукционной модели
принятия решений на основе таблиц решений // Автоматика и Телемеханика, №10,
2001, с. 78-90.
2. Леоненков А. В. Нечёткое моделирование в среде MATHLAB и fuzzyTECH. – СПб.: БХВ-Петербург, 2003, ISBN 5-94157-087-2.
3.
Pawlak Z. Rough Sets //
International Journal of Computer and Information Science, № 11, 1981, p.
341-356.
4. Виноградов О.В. Разработка и реализация методов
обработки баз знаний для систем поддержки принятия решений реального времени //
Тезисы докладов XIV Международной студенческой
школы-семинара «Новые информационные технологии» – М.: МИЭМ, 2006, ISBN 5-94506-138-7, с. 213-214.