BC/NW 2006, №2, (9) :4.6

 

РЕАЛИЗАЦИЯ ПРОТОТИПА РАСПРЕДЕЛЕННОГО ПЛАНИРОВЩИКА ДЛЯ СИСТЕМ ПОДДЕРЖКИ ПРИНЯТИЯ РЕШЕНИЙ

 

А.Ю. Неделина

 

(Москва, Московский Энергетический Институт (Технический Университет), Россия)

 

Интеллектуальное планирование - поиск оптимальной или допустимой  последовательности действий для достижения поставленной цели или разрешения возникшей проблемной ситуации в системах поддержки принятия решений реального времени (СППР РВ), относится к классу задач большой размерности, для которой существенным является время поиска решений. Решение подобных задач с ограничениями реального времени возможно лишь с использованием современных параллельных технологий, позволяющих существенно сократить общее время решения задачи.

В данной статье представлены результаты тестирования и характеристики ускорения для блока поиска решения планировщика DIPLAN (Distributed Planner), основанного на использовании распределенного подхода к решению задачи интеллектуального планирования.

 

Задача планирования для разрабатываемого планировщика рассматривается как задача поиска решения (построения плана действия) в пространстве состояний.

Пространство состояний в планировщике представляется в виде дерева T = (V, E),  представленного на рис. 1., где множество вершин V – состояния системы, а множество ветвей EÎ(V´V) – операторы (действия в системе). Ветви отражают действия или изменения в системе, активизирующие переход из одного состояния в другое.

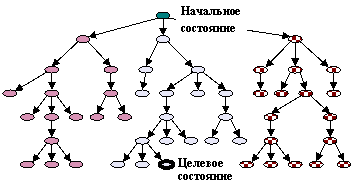
Рис.1. Пример дерева состояний

Задача планирования в контексте разрабатываемого планировщика DIPLAN состоит в поиске оптимального (кратчайшего) пути, ведущего из начального состояния (корня дерева) в одно из целевых.

Наиболее эффективные методы поиска достижения поставленной цели в пространстве состояний – это эвристические методы поиска [1]. Однако большая размерность задач и, как следствие, высокая трудоемкость вычислений существенно снижают применимость эвристических алгоритмов в интеллектуальных системах типа СППР РВ, где временной фактор является одним из определяющих.

В работе предложено следующее решение проблемы – разработка и реализация параллельных алгоритмов эвристического поиска, позволяющих распределить дерево поиска на поддеревья и обрабатывать поддеревья независимо друг от друга отдельными процессорами (см. рис. 1).

Основной функциональной компонентой планировщика DIPLAN является блок поиска решения [2]. Для блока поиска решения планировщика был предложен и реализован параллельный алгоритм итеративного поиска в глубину IDA* (Iterative-Deepening A*), подробное описание которого представлено в [3].

В качестве области тестирования разработанного планировщика был выбран класс дискретных задач оптимизации, которые могут быть определены в терминах поиска решения по дереву состояний.

Для тестирования и последующей оценки полученных результатов в качестве тестовой задачи (benchmark) использовалась n´n-головоломка при n=4 (15-Puzzle). Исходя из тестовой задачи, выбрана эвристическая функция Manhattan-Distance, оценивающая сумму кратчайших расстояний от ошибочно поставленных элементов до их целевого состояния.

, где

·        (ix,jx)- позиция элемента x в некотором состоянии, (i, j)– (номер строки, номер столбца);

·        (x DIV n, x MOD n)- позиция элемента x в целевом состоянии.

Приведем теоретические оценки вычислительной сложности предложенного параллельного алгоритма.

Трудоемкость последовательного IDA* алгоритма определяется следующей формулой  , где

·        kIDA* – количество раскрываемых вершин;

·        f(i) – оценочная MD-функция для i-й вершины.

Число раскрываемых вершин в алгоритме IDA* можно определить как  , при , где

·        b – эвристический фактор ветвления;

·        d – количество итераций.

В случае если b >1 для всех итераций, kIDA* раскрываемых вершин в итерации растёт экспоненциально с числом итераций d.

Следовательно, трудоемкость Tпос. мультипликативных операций последовательного IDA* для задачи n´n-головоломка можно оценить следующим выражением:

, при .

          Трудоемкость параллельной версии IDA* алгоритма вычисляется следующим образом:

, где p –количество процессоров;

Ускорение sp(p) параллельного выполнения IDA* алгоритма на p процессорах согласно закону Амдаля, имеет следующий вид:

, при  и n ≥4. 

Таким образом, ускорение , получаемое при параллельном выполнении разработанного IDA* алгоритма, зависит только от числа процессоров.

 

Реализация блока поиска решения с использованием параллельной версии IDA* алгоритма и эвристической MD-функции была выполнена в среде Visual C++ 6.0 средствами параллельной технологии MPI с применением пакета mpich.nt.1.2.5.

 Для тестовой задачи 4´4-головоломка было проведено 100 экспериментов в режиме моделирования параллельных вычислений на одном, 2-х и 4-х процессорах. Результаты 100 экспериментов были усреднены и разбиты на пять групп.

Графики зависимости времени вычисления решения и зависимости ускорения решения в блоке поиска решения для 4´4-головоломки представлены на рис. 2.

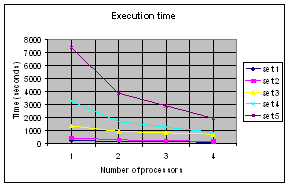
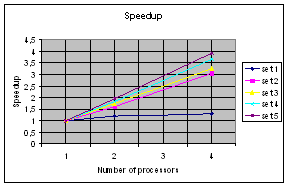
Рис. 2. Характеристики реализации блока поиска решения

Результаты моделирования блока поиска решения показали, что для задач с большим поисковым пространством параллельная обработка информации позволяет получить приемлемые для практики временные оценки процесса поиска решения.

 

В дальнейшем планируется продолжить исследования в 2-х направлениях: расширить класс тестовых задач, а также исследовать теоретически и экспериментально реализацию блока поиска решения применительно к параллельным архитектурам с общей памятью, а именно SMP системам.

Автор     выражает     благодарность    за    помощь    в      проведении

исследований д.т.н. проф. А.П. Еремееву кафедры “Прикладной  Математики”

(МЭИ ТУ, Россия),  а  также,   д.т.н. проф.  В. Фенглеру   и  доц.  Р. Кнауфу кафедр      “Вычислительной    техники”   и   “Искусственного  интеллекта” (ТУ Ильменау, Германия).

ЛИТЕРАТУРА

1.

Nilsson N., Principles of Artificial Intelligence, Tioga, Palo Alto, CA, 1980.

2.

Неделина А.Ю., “ Разработка распределенной архитектуры системы реального времени для решения задачи интеллектуального планирования”, Международный форум информатизации МФИ-2005, Доклады международной конференции «Информационные средства и технологии», в 3-х томах, Т.2-М.: Янус-К, 2005, С. 63 - 67.

3.

Eremeyev A.P., Nedelina A.Yu., Methods and algorithms of strategic planning for decision support systems, Proc. of the 6 Joint Conference on Knowledge-Based Software Engineering, IOS Press, 2004, С. 247-252.