BC/NW 2006, №2, (9) :4.8
РАСЧЕТЫ РАЗРЕЖЕННОЙ МАТРИЦЫ ПЛОТНОСТИ
МЕТОДОМ ОЧИСТКИ НА КЛАСТЕРНЫХ СИСТЕМАХ
А.М.Чернецов, О.Ю. Шамаева
(Москва, Московский энергетический институт
(Технический университет), Россия)
В докладе представлены результаты параллельного расчета на кластерных
системах молекулярных систем большой размерности методом очистки с учетом
свойств разреженности матрицы плотности.
Актуальность и вычислительная сложность расчетов электронной структуры
молекул рассматривалась подробно в [1]. Для сверхбольших молекулярных систем
целесообразно применение полуэмпирических квантово-химических методов в
приближении нулевого дифференциального перекрывания [2], в общем случае имеющих
асимптотическую сложность расчета O(N3),
где N – размерность базиса, пропорциональная числу атомов.
Асимптотическая сложность определяется диагонализацией матрицы фокиана
(решением симметричной проблемы собственных значений) и для сверхбольших
молекул неприемлема даже при расчетах на суперЭВМ.
В работе на основе метода Пальцера-Манолополиса
(метода очистки) [3] предложен параллельный алгоритм расчета для разреженных
матриц с блочно - трехдиагональным портретом, который реализован на языке
Фортран 95 с использованием средств MPI. Такую структуру матрицы имеют
некоторые классы органических соединений, например полимеры, линейные
несвёрнутые протеины и крупные фрагменты линейных цепей ДНК/РНК.
Для
расчета физико-химических свойств нужны не сами собственные векторы, а матрица
плотности P, являющаяся функцией от них.
Современным методом прямого нахождения P, обеспечивающим линейное
масштабирование времени расчета с ростом N при использовании технологии разреженных матриц,
является метод Пальцера-Манолополиса. В этом методе формула для итерационного нахождения
матрицы плотности P выглядит
следующим образом:
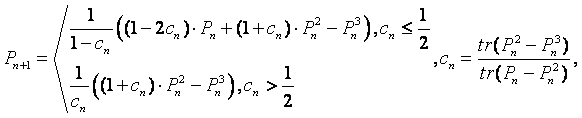 где n –
номер
шага итерационного процесса уточнения Р,
где n –
номер
шага итерационного процесса уточнения Р,
tr(Р) - след матрицы Р.
В качестве начального приближения Р0 выбирается нормализованный
масштабированный фокиан, сконструированный таким образом, что все его
собственные значения содержатся на отрезке [-1,1].
Оценивание минимального и
максимального собственных значений производится по методу кругов Гершгорина
[4].
При
расчетах матрицы плотности P
свойство разреженности матрицы позволяет сократить вычислительную сложность и
требуемый объем памяти.
В
рассматриваемой задаче матрица имеет сложную структуру разреженности.
На
данном этапе исследований рассматривались разреженные блочно-трехдиагональные
матрицы, которые описывают достаточно широкий класс полипептидов.
При умножении
трехдиагональных матриц в результирующей матрице появляется еще одна ненулевая
блочная диагональ. Однако, исходя из квантово-химических свойств задачи,
подобное расширение ненулевых элементов обладает свойством затухаемости и его
влиянием можно пренебречь и рассматривать умножение только трех диагоналей.
При реализации метода Пальцера-Манолополиса для
плотных матриц [1] максимально возможная размерность матриц составляла
8500.
При использовании свойств разреженности матрицы
коэффициентов и при наличии оперативной памяти в узлах кластеров емкостью в
2 Гбайт можно производить вычисления матрицы P уже существенно большей размерности, порядка 150000
орбиталей.
Тестирование разработанной программы проводилось в двух вычислительных
кластерах: на базе процессоров Intel Xeon Pentium 4/2.6 ГГц и суперкомпьютере МВС-6000IM с использованием в обоих случаях коммуникационной
технологии Myrinet 2000.
В суперкомпьютере МВС-6000IM
используются двухпроцессорные узлы на базе микропроцессоров Intel Itanium 2 /1.6 ГГц. с
кэш памятью 3-го уровня в 3 Мб.
Для молекулы с размерностью базиса в 7500 орбиталей
при использовании кластера на базе Intel Xeon/2.6 ГГц
время расчета методом Пальцера-Манолополиса в разреженной модификации по
сравнению со стандартной диагонализацией Хаусхолдера уменьшилось приблизительно
в 220 раз (время диагонализации 3700 сек, время разреженного метода - 17 сек). Измерение ускорений, достигаемых при
распараллеливании программы, производилось на тестовой матрице фокиана с
размерностью базиса, равной 75000.
На рис.1 приведены графические иллюстрации результатов
для двух используемых вычислительных кластеров, а также оценка ускорения,
полученная теоретически по закону Амдаля.
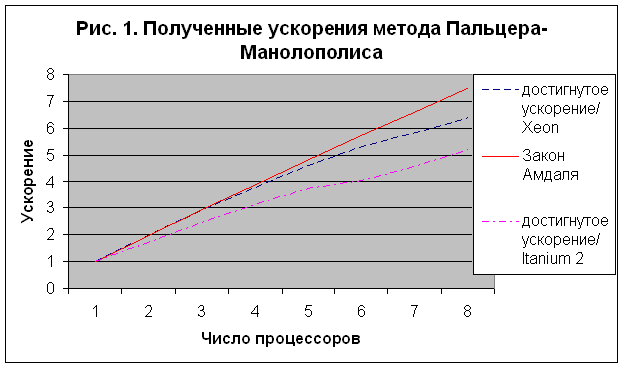
Для
метода Пальцера-Манолополиса с учетом разреженности матрицы коэффициентов для Xeon
достигнутое ускорение на 2 процессорах составляет 1.98, на 4 процессорах -3.8,
на 6 процессорах - 5.3 раза.
Соответствующие величины для Itanium 2 – 1.7 для двух, 3.1 – для четырех и 4.0 раза - для
6 процессоров.
При тестировании на Xeon процессы запускались по одному на узел, на Itanium 2 – по 2
процесса на узел. На суперкомпьютере МВС-6000IM полученные значения ускорения ниже по сравнению с Xeon, что объясняется
более высокой производительностью Itanium 2 и недостаточной пропускной способностью общей шины, а также конфликтами
доступа в оперативную память при использовании в узлах сразу двух процессоров.
Можно сравнить полученные значения ускорений для Xeon с результатами лучшего зарубежного коммерческого программного продукта MOPAC2002 [5]. Для молекулы фуллерена С960 с размерностью базиса 3840 орбиталей достигнутое на системе Origin 300 ускорение при числе процессоров до 8 ниже, чем в разработанной нами программе. При этом процессоры в кластере Origin 300 медленнее, чем использованные в кластере на базе Xeon, а межсоединение узлов – наоборот, существенно быстрее, что повышает достигаемое в MOPAC2002 ускорение.
В дальнейшем предполагается расширить класс рассматриваемых
разреженных структур матрицы плотности и разработать соответствующие
эффективные алгоритмы их расчетов.
Авторы выражают благодарность ВЦ РАН за возможность
использования его кластерных ресурсов для отладки и тестирования программы.
Работа поддержана РФФИ, проект 04-07-90220.
ЛИТЕРАТУРА
1.
Чернецов А.М.,
Шамаева О.Ю. Параллельная реализация метода Пальцера-Манолополиса для
вычисления матрицы плотности в задачах расчета электронной структуры молекул.
Труды международной конференции “Информационнные средства и технологии”, 18-20
октября
2.
Степанов Н.Ф.
Квантовая механика и квантовая химия. – Изд-ва “Мир” и “МГУ”, М., 2001, 518 с.
3. Anders M.N. Niklasson, C.J. Tumczak, Matt Challacombe. Trace resetting density matrix purification in
O(N) self-consistent-field theory J. of Chemical Physics, v. 118 N 15, 2003, pp
1-10.
4. Амосов А.А., Дубинский Ю.А.,
Копченова Н.В. Вычислительные методы
для инженеров. М., Высшая школа, 1994, 544 с.
5. SGI Computational Chemistry Applications Performance Report. Spring
2002, Silicon Graphics, Inc., 2002.